1.2 Error Explosion
1.2 Error Explosion Before we look at a much more dramatic example of roundoff errors, one that does not involve any loops , let's define a few terms:
Relative error is the ratio of the absolute error to the correct value. We can compare different errors meaningfully by comparing their relative errors. A percentage error expresses a relative error as a percentage. For example, we saw how If we assume that we're doing some computation whose correct result should be Program 1-2 performs these computations , where variable a equals Listing 1-2 Roundoff errors. package numbercruncher.program1_2; /** * PROGRAM 1-2: Roundoff Errors * * Demonstrate how a tiny roundoff error * can explode into a much larger one. */ public class RoundoffErrors { public static void main(String args[]) { float denominator = 20000000; float a = 10000001/denominator; float b = 1/2f; float diff1 = Math.abs(a - b); float pctError1 = 100*diff1/b; float inverse = 1/diff1; float diff2 = Math.abs(inverse - denominator); float pctError2 = 100*diff2/denominator; System.out.println(" a = " + a); System.out.println(" b = " + b); System.out.println(" diff1 = " + diff1); System.out.println("pctError1 = " + pctError1 + "%"); System.out.println(); System.out.println(" inverse = " + inverse); System.out.println(" diff2 = " + diff2); System.out.println("pctError2 = " + pctError2 + "%"); System.out.println(); System.out.println(" factor = " + pctError2/pctError1); } } Output: a = 0.50000006 b = 0.5 diff1 = 5.9604645E-8 pctError1 = 1.1920929E-5% inverse = 1.6777216E7 diff2 = 3222784.0 pctError2 = 16.11392% factor = 1351733.6 We see in Listing 1-2 that diff1, which should be Let's first examine the value of diff1. We lose all of the correct digits and end up with the incorrect one. The value of diff1 displays as 5.9604645E §C8 ?aonly the first of its eight digits is correct, since the exact value is 0.00000005, or 5.0E §C8 . The error in the value of diff1 comes from subtracting one value from another that is very close?ain this case,
Then, we proceed to compound the error. We know that dividing a numerator by a very small denominator (one close to 0) produces a quotient whose value is much larger than the numerator. The value of inverse is 1 divided by the value of diff1 . The value of diff1 is very small, and it is mostly wrong, so the division greatly magnifies the first error we got from the subtraction. Now, you may be thinking that this example is very contrived. Very true, but its point is to demonstrate that it's very possible to generate very large computational errors with just a few statements, even when the operations are mathematically correct. So, what can we do about cancellation errors? First of all, just knowing that they can happen is a major step. We need to be very wary of the results from subsequent calculations. But often, with some forethought, we can perform some algebraic manipulations and rewrite our algorithms to lessen or even avoid cancellation errors altogether. A classic example of how to do this is the hoary quadratic formula we learned in grade school to compute the two solutions to the equation ax 2 + bx + c = 0, where a If the value of 4 ac is very small compared with the value of b , then the value of In general, many roundoff errors can be prevented, or at least lessened, if we try to be smarter about how to code formulas into our programs. Chapter 4 has more to say about techniques for dealing with roundoff errors. |
| |
| Top |
EAN: 2147483647
Pages: 141


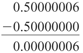
 0:
0: