1.2. Complexity and Construction
| | ||
| | ||
| | ||
1.2. Complexity and Construction
The recursive definition implies a recursive construction algorithm. Only the starting square must be chosen adequately. If the split operation cannot be performed well, the quadtree is unbalanced. Despite this effect, the depth of the tree is related to the distance between the points.
Theorem 1.1. The depth of a quadtree for a set P of points in the plane is at most log( s/c ) + 3/2, where c is the smallest distance between any two points in P, and s is the side length of the initial square.
The cost of the recursive construction and the complexity of the quadtree depends on the depth of the tree.
Theorem 1.2. A quadtree of depth d that stores a set of n points has O (( d + 1) n ) nodes and can be constructed in O (( d + 1) n ) time.
Due to the degree 4 of the internal nodes, the total number of leaves is one plus three times the number of internal nodes. Hence, it suffices to bound the number of internal nodes.
Any internal node v has one or more points inside Q ( v ). The squares of the node of a single depth cover the initial square. Therefore, at every depth, we have at most n internal nodes, which gives the node bound.
The most time-consuming task in one step of the recursive approach is the distribution of the points. The amount of time spent is linear only in the number of points and the O (( d + 1) n ) time bound holds.
The 3D equivalents of quadtrees are octrees . The quadtree construction can be easily extended to octrees in 3D. The internal nodes of octrees have eight children, and the children correspond to boxes instead of squares.
Neighbor finding. A common task when utilizing quadtrees is neighbor finding (also called navigation ), i.e., given a node v and a direction north, east, south or west, find a node v so that Q ( v ) is adjacent to Q ( v ). Normally, v is a leaf and v should be a leaf as well, but this is not necessarily unique. Obviously, one square may have many such neighbors, as shown in Figure 1.2.
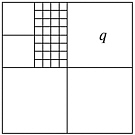
Figure 1.2: The square q has many west neighbors.
For convenience, we extend the neighbor search. The given node can also be internal; that is, v and v should be adjacent corresponding to the given direction and should also have the same depth. If there is no such node, we want to find the deepest node whose square is adjacent.
The algorithm works as follows . Suppose we want to find the north neighbor of v . If v happens to be the SE or SW child of its parent, then its north neighbor is easy to findit is the NE or NW child of its parent, respectively. If v itself is the NE or NW child of its parent, then we proceed as follows. Recursively find the north neighbor of
EAN: N/A
Pages: 69