List of Figures

Chapter 1: Quadtrees and Octrees

Figure 1.1: An example of a quadtree.

Figure 1.2: The square q has many west neighbors.

Figure 1.3: A terrain (left), a TIN of its height field (middle), and a superposition (right) [Wahl et al. 04]. (See Color Plate I.)

Figure 1.4: In order to use a quadtree for defining a height field mesh, it should be balanced. ( Courtesy Prof. R. Klein and R. Wahl, Bonn University.)

Figure 1.5: A quadtree defines a recursive subdivision scheme yielding a 4-8 mesh. The dots denote the newly added vertices. Some vertices have degree 4, and some have 8 (hence the name ).

Figure 1.6: The 4-8 subdivision can be generated by two interleaved quadtrees. The solid lines connect siblings that share a common parent. (See Color Plate II.)

Figure 1.7: The red quadtree can be stored in the unused ghost nodes of the blue quadtree. (See Color Plate III.)

Figure 1.8: A scalar field is often given in the form of a curvilinear grid. By doing all calculations in computational space, we can usually save a lot of computational effort.

Figure 1.9: Cells straddling the isosurface are triangulated according to a look-up table. In some cases, several triangulations are possible, which must be resolved by heuristics.

Figure 1.10: Octrees offer a simple way to compute isosurfaces efficiently ..

Figure 1.11: Volume data layout should match the order of traversal of the octree.

Figure 1.12: Ray shooting can be implemented efficiently with a grid.

Figure 1.13: The same scenario utilizing an octree.

Figure 1.14: Line parameters are trivial to compute for children of a node.

Figure 1.15: The sub- cell that must be traversed first can be found by simple comparisons. Here, only the case 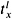> 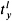is depicted.

Figure 1.16: Sub-cells are numbered according to this scheme.

Figure 1.17: With the direction cube, we can discretize directions and organize them with any hierarchical partitioning scheme.

Figure 1.18: A uv interval on the direction cube plus a xyz interval in 3-space yield a beam.

Figure 1.19: By sorting objects within each 5D leaf, we can often stop checking ray intersection quite early.

Figure 1.20: By truncating the beam (or rather, the list of objects), we can save a lot of memory usage of a 5D octree, while reducing performance only insignificantly.

Chapter 2: Orthogonal Windowing and Stabbing Queries

Figure 2.1: An example of the node information in an interval tree. For convenience, the intervals are represented by 2D line segments. The left and right endpoints l _i and r _i of the segments s _i hit by the median x _med are represented in sorted lists M _L and M _R , respectively.

Figure 2.2: A segment tree for a set of segments. The segment s is minimally covered by the nodes v ₁ , v ₂ , v ₃ , and v ₄ .

Figure 2.3: The query procedure for a segment tree and a query line l. The shaded intervals indicate the query path from the root to the leaf. All segments stored at the corresponding nodes are reported .

Figure 2.4: A stabbing query for a set of bounding boxes can report all polygonal objects near q.

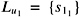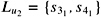Figure 2.5: Some parts of the multi-level segment tree of four boxes in 2D. The segment tree T ¹ and the relevant trees for the nodes u ₁ and u ₂ with and for the query point q are shown.

Figure 2.6: A 2D kd-tree and a rectangular range query. Each node corresponds to a split line. Additionally, each node represents a unique rectangular range R(v) according to the path from the root to the node.

Figure 2.7: Every node v in the one-dimensional search tree represents a unique interval v.I. A query interval I is uniquely covered by a minimal set of intervals v.I.

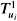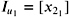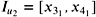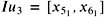Figure 2.8: Some parts of the 2D range tree of eight points in 2D. The range tree T ¹ and the relevant trees for the nodes u ₁ , u ₂ , and u ₃ with , , and for the query rectangle R = I ₁ — I ₂ with intervals I ₁ X and I ₂ Y.

Figure 2.9: The box B _i reported by a (axis-parallel box/ axis-parallel box) windowing query for B contains B for i = 1, has a vertex inside B for i = 2, and has a segment that crosses B for i = 3.

Figure 2.10: A rectangular range query by an infinite box grounded in s will answer the windowing query in the third case.

Figure 2.11: At the node v with a median v. x _med in an interval tree, there is also a 2D range tree v. M _L of the left endpoints of the segments in v. S _med . v. M _L answers the query [y _l , y _u ] — [ ˆ ˆ , x] for a segment s = [(x, y _l ), (x, y _u )].

Figure 2.12: The texture synthesis algorithm proceeds in scan line order through the texture and considers only the neighborhood around the current pixel as shown.

Figure 2.13: Using an image pyramid, the texture synthesis process becomes fairly robust against different scales of detail in the sample images.

Figure 2.14: Some results of the texture synthesis algorithm [Wei and Levoy 00]. In each pair, the image on the left is the original one, and the one on the right is the (partly) synthesized one. (See Color Plate IV.) (Courtesy of L.-Y. Wei and M. Levoy, and ACM.)

Figure 2.15: The shape distributions of a number of different simple objects. (See Color Plate XX.)

Chapter 3: BSP Trees

Figure 3.1: An example of a BSP tree for a set of objects.

Figure 3.2: Left: an auto-partition. Right: an example of a configuration in which any auto-partition must have quadratic size .

Figure 3.3: BSP trees are an efficient data structure encoding visibility order of a set of polygons.

Figure 3.4: Each leaf cell of the BSP representation of an object is completely inside or completely outside.

Figure 3.5: Using BSPs, we can efficiently compute these Boolean operations on solids.

Figure 3.6: The fundamental step of the construction is this simple operation, which merges a BSP and a plane.

Figure 3.7: The main building block of the algorithm consists of these four cases (plus analogous ones).

Figure 3.8: Computation of Boolean operations is based on a general merge operation.

Figure 3.9: A graphical depiction of the merge step in the algorithm for Boolean operations on objects represented by BSP trees.

Chapter 4: Bounding Volume Hierarchies

Figure 4.1: Some bounding volumes . (Courtesy of Blackwell Publishing.)

Figure 4.2: One way to define tightness is via the directed Hausdorff distance.

Figure 4.3: The tightness of an AABB remains more or less constant xhroughout the levels of an AABB hierarchy for surfaces of small curvature.

Figure 4.4: The tightness of an OBB decreases for deeper levels in an OBB hierarchy for small curvature surfaces

Figure 4.5: A simple greedy strategy can produce much dead space.

Figure 4.6: A less greedy strategy combines bounding volumes by computing a tiling.

Figure 4.7: The probability of a ray hitting a child box can be estimated by the surface area.

Figure 4.8: By estimating the volume of the Minkowski sum of two BVs, we can derive an estimate for the cost of the split of a set of polygons associated with a node. (See Color Plate V.)

Figure 4.9: Algorithm for applying the splitting criterion to BVH construction.

Figure 4.10: If the deformation is a predefined morph, then a BVH for in-between objects can be constructed by morphing the BVs. (Courtesy of Blackwell Publishing.)

Figure 4.12: The bounding volume test tree is induced by the simultaneous traversal of two BVHs. (Courtesy of the editors of the Proceedings of Vision, Modeling, and Visualization 2003.)

Figure 4.11: Hierarchical collision detection can discard many pairs of polygons with one bounding volume check. Here, all pairs of polygons from A ₁ and B ₂ can be discarded.

Figure 4.13: Left: thought experiment illustrating our approach to estimate the probability of an intersection between the surfaces contained a pair of bounding volumes during traversal. Middle: practical case, defined as collision cell. Right: definition of a well-filled cell.

Figure 4.14: The (conceptual) idea of the time-critical collision detection method is to count the number of cells that are well-filled by polygons from A and from B. (Courtesy of Blackwell Publishing.)

Figure 4.15: During BVH construction, we determine the overall number of cells inside bounding volume A that are well-filled.

Figure 4.16: The balls-into- bins model. (Right image courtesy of Animation Factory.)

Figure 4.17: Running time (left) and error (right) of an example implementation of time-critical collision detection. (Objects: two copies of a car body, 60,000 polygons each.)

Chapter 5: Distance Fields

Figure 5.1: Example of a distance field in the plane for a simple polygon (thick black lines). The distance field inside the polygon is not shown. The dashed lines show the Voronoi diagram for the same polygon. The thin lines show isosurfaces for various isovalues. (See Color Plate VI.)

Figure 5.2: The vector distance field for the same polygon as shown on the left. Only a few vectors are shown, although (in theory) every point of the field has a vector. (See Color Plate VII.)

Figure 5.3: A network of roads described in the plane by a set of edges (left) and the distance map of these roads . The distance of each point in the plane from a road is color-coded. It could be used, for example, to determine the areas where new houses can be built. (See Color Plate VIII.)

Figure 5.4: Representing distance fields (left: 2D field of the number 7, 262,144 distance samples) by octrees (right: quadtree cells are subdivided to their highest resolution along the boundary of the 2D shape, yielding 6681 cells) has both memory and computational advantages. (Courtey of Sarah Frisken, Tufts University, and Ronald Perry, Mitsubishi Electric Research Laboratories.)

Figure 5.5: By convoluting a distance matrix with an initially binary distance field (0 or ˆ ), one gets an approximate distance field. Here, a 5 — 5 — 5 example of such a matrix is shown.

Figure 5.6: (left) The distance function of a point site in the plane is a cone. (middle) More complex sites have a bit more complex distance functions. (right) The distance function of sites in 3D is different for the different slices of the volume [Hoff III et al. 99]. (See Color Plate IX.) (Courtesy of K. Hoff, T. Culver, J. Keyser, M. Lin, and D. Manocha, Copyright ACM.)

Figure 5.7: By specifying correspondences, the user can identify feature points that should transition into each other during the morph [?]. (Courtesy of Daniel Cohen-Or.)

Figure 5.9: Example of a 3D difference operation [Bremer et al. 02]. (Courtesy of Prof. Bremer et al.)

Figure 5.10: Close-up view showing the adaptivity [Bremer et al. 02]. (Courtesy of Prof. Bremer et al.)

Figure 5.8: Example of difference of two DFs. On the left, the two DFs for tool and object are shown superimposed; on the right, the result is shown.

Chapter 6: Voronoi Diagrams

Figure 6.1: The Voronoi diagram of a set of sites in the Euclidean plane.

Figure 6.2: The Voronoi diagram and the Delaunay triangulation of a set of sites in the Euclidean plane.

Figure 6.3: Adequately shrinking the circumcircle Circle(p _j , p _k , p _l ) and holding the contact with p _j shows that there is a circle inside Circle(p _j , p _k , p _l ) that has only p _j and p _i on its boundary.

Figure 6.4: An edge flip between p _i q and p _l p _k .

Figure 6.5: Every circle passing through p _k and p _l will contain either p _i or q. If q , p _i , p _l , and p _k are in non-convex position, then Circle(p _i , p _l , p _k ) cannot contain q because the tangent t _pk blocks q .

Figure 6.6: Successively check the outer triangles of P( ˜… (p _i )) for conflicts with p _i. The point r is the last point that will evoke an edge flip.

Figure 6.7: If p _i is outside the convex hull of DT _{i ˆ1} , the starting ˜… (p _i ) is given by the visible points on the hull ^. P ˜… (p _i )) is a convex chain opposite p _i .

Figure 6.8: The Delaunay DAG stores the history of all triangles ever constructed.

Figure 6.9: The tetrahedron (p _j , p _k , p _l , p _m ) contains p _i and four edges p _i p _j , p _i p _k , p _i p _l , and p _i p _m are inserted. For every face of P( ˜… (p _i )), we check the outer tertrahedra; in this case, (p _j , p _l , p _m , q) with the opposite p _i .

Figure 6.10: The first figure shows the 2 3 edge flip, whereas the second figure shows a 3 2 edge flip. The ground face G is flippable because the endpoints of G, p _i , and q are in convex position. New triangles (shaded) of P( ˜… (p _i )) opposite p _i are found after the flipping.

Figure 6.11: The projection of points from 2D onto the paraboloid in 3D. The lower convex hull on the paraboloid can be projected back to 2D and represents the Delaunay triangulation in 2D. In general, the Delaunay triangulation in 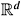is equivalent to the convex hull in 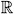^{d +1} .

Figure 6.12: The constrained Voronoi diagram ConstrVD(S, L) and its dual.

Figure 6.13: Bisectors under L ₁ and L ₂ distance functions. One can build the bisector by the intersections of scaled copies of the unit circle.

Figure 6.14: Voronoi diagrams under L ₁ and L ₂ distance functions.

Figure 6.15: Bisectors under convex distance functions.

Figure 6.16: The Voronoi diagram of a set of sites on a graph.

Figure 6.17: The Voronoi diagram of a set of non-intersecting polygonal objects.

Figure 6.18: The Voronoi diagram with additive weights.

Figure 6.19: The 3-order Voronoi diagram.

Figure 6.20: The farthest color Voronoi diagram.

Figure 6.21: After constructing a sorted list of slabs and a sorted list of segments in every slab, a query point q can be located quickly by a binary search.

Figure 6.22: The separating surfaces for a 3D slab subdivision of convex cells. The separator ƒ ₁₀ separates the cells C ₁ , C ₂ , , C ₁₀ from C ₁₁ , C ₁₂ , , C ₁₄ .

Figure 6.24: The binary separator tree for the cell decomposition of Figure 6.25. Every leaf represents a cell.

Figure 6.23: The separator ƒ ₁₀ of Figure 6.22 is a binary tree of its edges. From ƒ ₁₀ to ƒ ₉ , local updates are made.

Figure 6.25: The y order of the Voronoi sites gives the total order of the cell decomposition in 2D and 3D.

Figure 6.26: Roman mosaics from baths [Mosaic a, Mosaic b]. (See Color Plate X.) ((left) Courtsey of D. Mesher at the SJSU Jewish Studies program. (right) Courtesy of the Hellenic Ministry of Culture.

Figure 6.27: Example centroidal Voronoi diagram (CVD).

Figure 6.28: Example CVD with the Manhattan metric instead of the Euclidean metric.

Figure 6.29: Different shapes of cones embody different metrics.

Figure 6.30: The vector field for orienting the mosaic pieces can be computed by discrete gradients from a set of curves [Hausner 01]. (Courtesy of Alejo Hausner and ACM.)

Figure 6.31: Process to preserve edges of the original image in the final mosaic. [Hausner 01]. (See Color Plate XI.) (Courtesy of Alejo Hausner and ACM.)

Figure 6.32: Mosaics generated by randomly placing 6000 Voronoi sites on an image and coloring each Voronoi region uniformly by the color in the image. (See Color Plate XII.)

Figure 6.33: Two examples of mosaics [Hausner 01], generated with the CVD method. (See Color Plate XIII.) (Courtesy of Alejo Hausner and ACM.)

Figure 6.34: Inserting P changes the Voronoi diagram. The thick and dashed lines together constitute the Voronoi diagram over 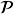, while the thick and the thin lines show the Voronoi diagram over 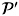. The thin lines alone represent the Voronoi region for P, the point at which the interpolation is to be computed.

Chapter 7: Geometric Proximity Graphs

Figure 7.1: Identifying all pairs of close nodes in a set can reveal significant structure, such as a molecule or a mobile ad-hoc network. However, care must be exercised when establishing that proximity is indeed relevant (Cassiopeia courtesy of [RAS]).

Figure 7.2: Proximity graphs can even help in psychology to explain some optical illusions.

Figure 7.3: The lune is the defining neighborhood of the relative neighborhood graph.

Figure 7.4: The defining neighborhood for the Gabriel graph is the diameter sphere.

Figure 7.5: The sphere-of-influence graph is defined by spheres of influence around each point.

Figure 7.6: Examples of the family of lunes that define the -skeleton.

Figure 7.7: Examples of proximity graphs.

Figure 7.8: The 3-SIG over the same point cloud as in Figure 7.7.

Figure 7.9: The 3-SIG with additional pruning.

Figure 7.10: Example DG and MST for the same set of points as in Figure 7.7.

Figure 7.11: A simple heuristic leads to an O(dn ² ) algorithm to construct the GG.

Figure 7.12: The nearest -neighbor yields a simple classifier.

Figure 7.13: Comparison of the decision boundaries induced by the (optimal) Bayes classifier (squares), and the nearest-neighbor classifier (triangles).

Figure 7.14: Conceptually, the nearest-neighbor classifier partitions the feature space into Voronoi cells. (See Color Plate XIV.)

Figure 7.15: The decision boundary of the nearest-neighbor classifier runs between Delaunay neighbors with different colors. (See Color Plate XV.)

Figure 7.16: The edited training set has the same decision boundary but fewer nodes. (See Color Plate XVI.)

Figure 7.17: Delaunay editing often leaves too many points in the edited set. The unfilled points will be removed by Delaunay editing, but the contribution of the circled points is questionable.

Figure 7.18: Different proximity graphs yield different edited (i. e., reduced) training sets and, thus, different approximations to the decision boundary.

Figure 7.19: 3D scanners (left) produce large point clouds (right) from real objects (middle).

Figure 7.20: Different weight functions ( kernels ). Note that the horizontal scale of the Gauss curve is different, so that the qualitative shape of the curves can be compared better.

Figure 7.21: Visualization of the implicit function f(x) over a 2D point cloud. Points x ˆˆ 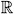² with f(x) ‰ˆ 0, i.e., points on or close to the surface, are shown magenta . Red denotes f(x) ‰ 0, and blue denotes f(x) ‰ 0. (a) point cloud; (b) reconstructed surface using the definition of [Adamson and Alexa 03]; (c) utilizing the centered covariance matrix produces a better surface, but it still has several artifacts; (d) surface and function f(x) based on the SIG. (See Color Plate XVII.) (Courtesy of Elsevier.)

Figure 7.22: A proximity graph can help to improve the quality of the implicit surface by approximation of the geodesic distance instead of the Euclidean distance. (Courtesy of Elsevier.)

Figure 7.23: Reconstructed surface based on simple WLS and with proximity graph (rightmost) for a noisy point cloud obtained from the 3D Max Planck model (leftmost). Notice how fine details, as well as sparsely sampled areas, are handled without manual tuning. (See Color Plate XVIII.) (Courtesy of Elsevier.)

Figure 7.24: Automatic sampling density estimation for each point allows you to determine the bandwidth automatically and independently of scale and sampling density (middle), and to detect boundaries automatically (right). (See Color Plate XIX.) (Courtesy of Elsevier.)

Figure 7.25: Outline of the point-cloud intersection detection.

Figure 7.26: Two point clouds A and B and their intersection spheres I ₁ and I ₂ .The root-finding procedure, when initialized with p ₁ , p ₂ ˆˆ A, will find an approximate intersection point inside the intersection sphere I ₁ .

Figure 7.27: If the spherical neighborhoods C _i (filled disks) are too small, not all collisions can be found. (i) Adjoining neighborhoods might not overlap sufficiently, so their intersection contains no randomly chosen cloud point. (ii) The surface might not be covered by neighborhoods C _i .

Figure 7.28: Models with boundaries can cause errors (I ₁ could remain undetected), which can be avoided by virtual edges in the proximity graph.

Figure 7.29: An intersection sphere centered at an AIP p _i . Its radius r can be determined approximately with the help of a second point on the other side of B.

Figure 7.31: One of the test objects for Figure 7.30. (See Color Plate XXI.)

Figure 7.30: The plot shows the running time depending on the size of the point clouds for two objects (see Figures 7.19 and 7.31). The time is the average of all intersection detection times for distances between 0 and 1.5 and a lot of different orientations for two identical copies of each object.

Chapter 8: Kinetic Data Structures

Figure 8.1: Example of a segment tree.

Figure 8.2: An example of a segment tree over four segments. The dashed segments show the segments 4 and 2, respectively, after two of their endpoints have swapped position. The changes in the tree are highlighted with dashed boxes.

Figure 8.3: An example of a kinetic BSP tree. On the left, four segments are shown, together with the vertical splitting lines. At the top of each vertical line is its ID, which happens to also be the endpoints rank in the situation shown. On the right is the corresponding BSP tree; round nodes are vertical splitting nodes, while square nodes are multi-way (i.e., horizontal) nodes. Leaves are small grey nodes.

Figure 8.4: This is the first case of leaf operations to be performed on a kinetic BSP when an event happens. The leaf is replaced by a small subtree . Its root is a vertical node with a splitting line through p (the endpoint that has swapped ranks with another endpoint).

Figure 8.5: This is the second case of leaf operations when an event happens. Again, the leaf is replaced by a small subtree. However, here the exact operation depends on the type of parent node of . If the parent is a vertical node, then the new subtree is straightforward. If the parent is a multi-way (horizontal) node, then we must insert a new splitting line into that parent.

Figure 8.6: The properties of the new BSP are restored by pushing up the new fragment through the tree while merging it with other fragments of the same segment.

Figure 8.7: A simple example of a combinatorial restructuring of a kinetic BSP.

Chapter 9: Degeneracy and Robustness

Figure 9.1: The Voronoi diagram for a set of sites subdivides the plane into regions of the nearest neighborship.

Figure 9.2: The convex hull for a set of points is the smallest convex set that contains all points.

Figure 9.3: The arrangement of a set of segments represents a subdivision of the plane into cells represented by vertices and edges.

Figure 9.4: An edge of the arrangement and its information in the DCEL.

Figure 9.8: The DCEL information of a tetrahedron T. The faces F ₁ and F ₂ of the oriented edge e ₁ have next edge e ₅ and previous edge e ₆ .

Figure 9.5: The sweep status structure contains a sorted list of the segments met by the sweepline. At position i), a new segment has to be inserted and the intersections with its neighbors will create future events. At position ii), such a new event changes the order of the segments, intersections are computed, and further future events may be created.

Figure 9.6: The lines l ₁ : 4.3 — x/8.3 and l ₂ : 1.4 — x/2.7 appear to have several intersections using floating-point evaluation with base 10, precision 2, and round to nearest.

Figure 9.7: Cutting a polyhedron by a hyperplane.

Figure 9.9: Conversion cycle by rounding to nearest with a first-time error.

Figure 9.10: Conversion cycle by rounding to nearest with the correct result.

Figure 9.11: The scheme of the procedure GrowExpansion. (Redrawn and adapted courtesy of Jonathan Richard Shewchuk [Shewchuk 97].)

Figure 9.12: The addition scheme of ExpansionSum for two expansions 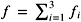and 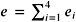. (Redrawn and adapted courtesy of Jonathan Richard Shewchuk [Shewchuk 97].)

Figure 9.13: The simple incremental adaptive approach collects the errors by magnitude on the lowest level. (Redrawn and adapted courtesy of Jonathan Richard Shewchuk [Shewchuk 97].)

Figure 9.14: The full incremental adaptive approach collects the errors by magnitude on every level. (Redrawn and adapted courtesy of Jonathan Richard Shewchuk [Shewchuk 97].)

Figure 9.15: The intermediate incremental adaptive approach approximates the errors T _i in a correction term . (Redrawn and adapted courtesy of Jonathan Richard Shewchuk [Shewchuk 97].)

Figure 9.16: The expression tree of .

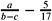Figure 9.17: Computing the area of a rectangle P.

Figure 9.18: The chain p, q, and r is clockwise if we look from the top. The vertex s lies below the oriented plane and O3D(p, q, r, s) is positive.

Figure 9.19: Projecting Circle(p, q, r) onto the paraboloid results in a set of points lying in a 2D plane.

Figure 9.20: How to compute the rotation angle . The angle is bigger than ₁ and ₂ for all p and q.

Figure 9.21: Two interactive approximative predicates overlap within a region.

Figure 9.22: The angular range ˆ  (a, b, c) and its measure