4.2. Updating for Morphing Objects
| | ||
| | ||
| | ||
4.2. Updating for Morphing Objects
When the geometry underlying a BVH has deformed, the original BVH is no longer valid. Basically, there are two options: rebuilding the BVH (possibly only partially) or refitting. In the latter case, the tree structure itself remains unchanged, and only the extents of the BVs are updated. Refitting is much faster, but the BVs are usually less tight and the overlap between siblings is larger.
An important case of deformation occurs in animation systems, where objects are deformed by morphing (or blending ), i. e., in-between objects are constructed by interpolating between two ore more morph targets. This usually requires the target models to have the same number of vertices and the same topology.
The idea of [Larsson and Akenine-Mller 03] is to construct one BVH (for one of the morph targets) and fit this to the other morph targets such that corresponding nodes contain exactly the same vertices. With each node of the BVH, we save all corresponding BVs (one from each morph target; see Figure 4.10). During runtime, we can construct a BVH for the morphed object just by taking the original BVH and interpolating the BVs.
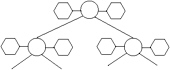
Figure 4.10: If the deformation is a predefined morph, then a BVH for in-between objects can be constructed by morphing the BVs. (Courtesy of Blackwell Publishing.)
Assume we are given n morph targets, O i , each with vertices ![]() , and n weight vectors
, and n weight vectors ![]() . Then each vertex v j of the morphed object is an affine combination
. Then each vertex v j of the morphed object is an affine combination
| (4.9) | |
Let D i be the n BVs of the corresponding nodes in the BVHs of the O i (i. e., all D i contain the same vertices, albeit at different positions ). We denote a DOP by ![]() , where
, where ![]() , is one interval of the DOP. Let b l ,l = 1 k, denote the set of orientations over which all DOPs are defined.
, is one interval of the DOP. Let b l ,l = 1 k, denote the set of orientations over which all DOPs are defined.
We can interpolate a new DOP ![]() , from these n DOPs by
, from these n DOPs by
| (4.10) | |
This interpolated DOP D will enclose all the interpolated vertices beneath its node, i. e.,
| (4.11) | |
Proof: For all v l ˆˆ D ,we have
| (4.12) | |
and similarly, we can bound v b j from above by e j .
This works just the same for AABBs, since AABBs are a special case of DOPs.
It also works for sphere trees. Let B i = ( c i , r i ) denote a sphere from the sphere tree of morph target O i . Then we can obtain the corresponding bounding sphere B = ( c , r ) by
| (4.13) | |
Proof: For all v l ˆˆ B , we have
| (4.14) | 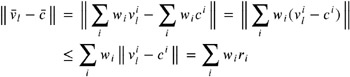 |
using the triangle inequality.
Overall, we can use existing top-down BVH traversal algorithms for collision detection. The only additional work that must be done is the interpolation, i. e., morphing of the BVs, just before they are checked for overlap. The exact positions of the morphed vertices enclosed by a bounding volume are not needed.
This deformable collision detection algorithm seems to be faster in practical cases, and its performance depends much less on the polygon count than the more general method presented in [Larsson and Akenine-Mller 01].
The method does have a few drawbacks:
-
Since it does not rebuild the BVH, one must somehow construct a BVH that yields good performance for all in-between models;
-
As explained, it works only for morphing schemes that allow only one weight per morph target. One could extend the technique to a more general morph scheme, where each target has a weight vector
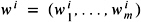 ( m = number of vertices). Then, however, we would have to morph the DOPs by
( m = number of vertices). Then, however, we would have to morph the DOPs by (4.15) 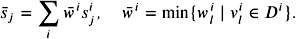
So, we would need to precompute and store those w i for each DOP D in the BVH. This may or may not be feasible in practice;
-
As we stated, it works for only certain kinds of deformations.
EAN: N/A
Pages: 69