6. Nonlinear Extension using Kernels

The Gaussian assumption implied by BDA does not hold in general for real world problems. In this section, we discuss a non linear extension of BDA using a kernel approach.

6.1 The Kernel Trick

For a comprehensive introduction to kernel machines and SVM, refer to [46]. Here we briefly introduce the key idea.

The original linear BDA algorithm is applied in a "feature space," ^[1] F, which is related to the original space by a nonlinear mapping

(30.17)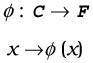

where C is a compact subset of R^N. However, this mapping is expensive and will not be carried out explicitly, but through the evaluation of a kernel matrix K, with components k(x_i, x_j) = φ ^T(x_i) φ(x_j). This is the same idea as that adopted by support vector machine [31], kernel PCA, and kernel discriminant analysis [48], [49].

6.2 BDA in Kernel Form

The trick here is to rewrite the BDA formulae using only dot-products of the form φi^Tφj.

Using superscript φ to denote quantities in the new space, we have the objective function in the following form:

(30.18)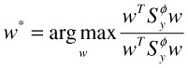

where

(30.19)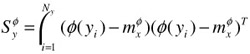

(30.20)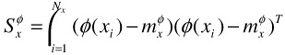

Here is the positive centroid in the feature space F. We will express it in matrix form for the convenience of later derivations:

(30.21)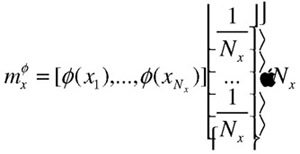

Since the solution for w is the eigenvector(s) corresponding to the nonzero eigenvalues of the scatter matrices formed by the input vectors φ(x_i) and φ(y_i) in the feature space F, the optimal w is in the subspace spanned by the input vectors in the feature space. Thus, we can express w as a linear combination of φ (x_i) and φ (y_i), and change the problem from finding the optimal w to finding the optimal a:

(30.22)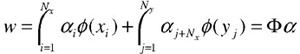

where

(30.23)

The numerator of (30.18), after being expressed as the negative scatter with respect to positive centroid in the feature space, can be rewritten as

(30.24)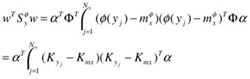

where

(30.25)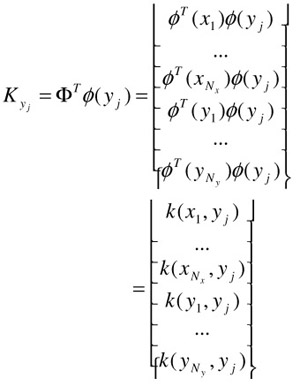

(30.26)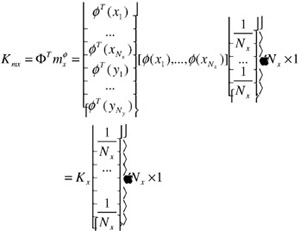

Both of these are vectors of dimension (N_x+N_y) 1, and K_x is of size (N_x+N_y) N_x, and is defined in Equation (30.30). We can further rewrite the summation term in the middle of Equation (30.24) into a matrix operation; this is done by realizing that for two sets of column vectors v_i and w_i in V = […, v_i, …] and W = […, w_i, …], we have

(30.27)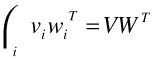

Therefore, the middle portion of Equation (30.24) is further written as

(30.28)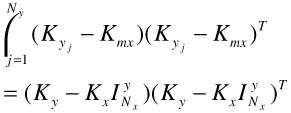

where

(30.29)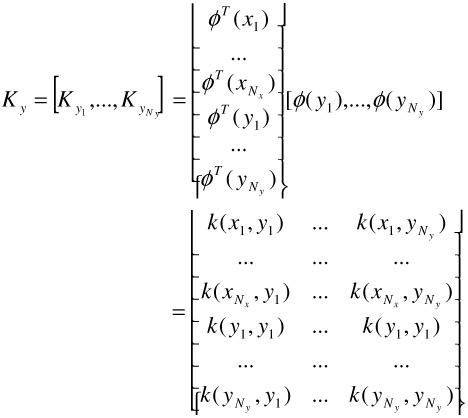

(30.30)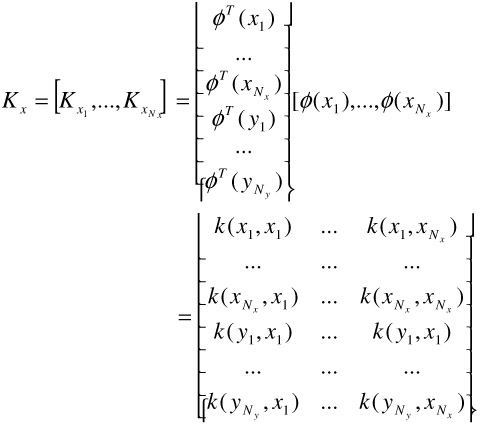

and is an N_x N_y matrix of all elements being .

Similarly, we can rewrite the denominator of (30.18):

(30.31)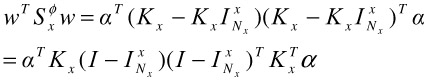

Here I is the identity matrix and is an N_x N_x matrix of all elements being .

Since = ()^T and ()^T = , the middle part of Equation (30.31) can be further expanded and simplified as

(30.32)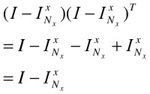

6.3 The Nonlinear Solution

To this point, by substituting Equations (30.24), (30.28), (30.31), and (30.32) into (30.18)–(30.20), we arrive at a new generalized Rayleigh quotient, and it is again a generalized eigen-analysis problem, where the optimal a's are the generalized eigenvectors associated with the largest eigenvalues λ's, i.e.,

(30.33)

With optimal a, the projection of a new pattern z onto w, ignoring weighting by square-rooted eigenvalue, is directly given by

(30.34)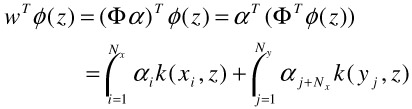

6.4 The Algorithm

When applied in a retrieval system as the relevance feedback algorithm, it can be briefly described as follows:

With only one query for the first round, it just retrieves the nearest Euclidean neighbors as the return. During following rounds of relevance feedback with a set of positive and negative examples, and a chosen kernel k, it will

Compute K_x and K_y as defined in Equation (30.29) and (30.30);
Solve for a's and λ's as in Equation (30.33);
With a's ordered in descending order of their eigenvalues, select the subset {a_i|λ_i> τ λ₁ }, where τ is a small positive number, say, 0.01;
a_i = a_i 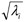, for selected a_i the previous step;
Compute the projection of each point z onto the new space as in Equation (30.34).
In the new space, return the points corresponding to the Euclidean nearest neighbors from the positive centroid.

^[1]A term used in kernel machine literature to denote the new space after the nonlinear transform—this is not to be confused with the feature space concept previously used to denote the space for features/descriptors extracted from the media data.