6.7 Using Protocols to Specify Situations
|
6.7 Using Protocols to Specify Situations
The use of protocols helps clarify what is going on in many examples. In this section, I illustrate this point with three examples, two of which were introduced in Chapter 1—the second-ace puzzle and the Monty Hall puzzle. The first (admittedly somewhat contrived) example formalizes some of the discussion in Chapter 3 regarding when conditioning is applicable.
6.7.1 A Listener-Teller Protocol
Suppose that the world is characterized by n binary random variables, X1,…, Xn. Thus, a world w can be characterized by an n-tuple of 0s and 1s, (x1,…, xn), where xi ∈ {0, 1} is the value of Xi at world w. There are two agents, a Teller, who knows what the true values of the random variables are, and a Listener, who initially has no idea what they are. In each round, the Teller gives the Listener very limited information: she describes (truthfully) one world that is not the true world. For example, if n = 4, the Teller can say "not (1, 0, 0, 1)" to indicate that the true world is not (1, 0, 0, 1).
How can this situation be modeled as a system? This depends on what the local states are and what protocol the Teller is following. Since the Teller is presumed to know the actual situation, her state should include (a description of) the actual world. What else should it include? That depends on what the Teller remembers. If she remembers everything, then her local state would have to encode the sequence of facts that she has told the Listener. If she does not remember everything, it might include only some of the facts that she has told the Listener—perhaps even none of them—or only partial information about these facts, such as the fact that all of the worlds mentioned had a 0 in the first component. The form of the local state affects what protocol the Teller could be using. For example, the Teller cannot use a protocol that says "Tell the Listener something new in each round" unless she remembers what she has told the Listener before.
For definiteness, I assume that the Teller remembers everything she has said and that the local state includes nothing else. Thus, the Teller's local state has the form (w0, 〈w1,…, wm〉), where w0 and, for i ≥ 1, wi is the world that the Teller said was not the actual world in round i. (Of course, since the Teller is being truthful, wi ≠ w0 for i ≥ 1.) For simplicity, I take the environment's state to be identical to the Teller's state, so that the environment is also keeping track of what the actual world is like and what the Teller said. (I could also take the environment state to be empty, since everything relevant to the system is already recorded in the Teller's state.)
What about the Listener? What does he remember? I consider just three possibilities here.
-
The Listener remembers everything that he was told by the Teller.
-
The Listener remembers only the last thing that the Teller said.
-
The Listener remembers only the last two things that the Teller said.
If the Teller's local state is (w0, 〈w1,…, wm〉) then, in the first case, the Listener's local state would be 〈w1,…, wm〉; in the second case, it would be just wm (and 〈〉 if m = 0); in the third case, it would be (wm−1, wm) (and 〈〉 if m = 0, and 〈w1〉 if m = 1). Since the environment state and the Teller's state are the same in all global states, I denote a global state as ( , (w0, 〈w1,…, wm〉),…) rather than ((w0, 〈w1,…, wm〉), (w0, 〈w1,…, wm〉),…), where exactly what goes into the ellipsis depends on the form of the Listener's state.
Just specifying the form of the global states is not enough; there are also constraints on the allowable sequences of global states. In the first case, a run r has the following form:
-
r(0) = ( , (w0, 〈〉), 〈〉),
-
if r(m) = ( , (w0, 〈w1,…, wm〉), 〈w1,…, wm〉), then r(m + 1) = ( , (w0, 〈w1,…, wm, wm+1〉), 〈w1,…, wm, wm+1〉) for some world wm+1.
The first component of the Teller's (and environment's) state, the actual world, remains unchanged throughout the run; this implicitly encodes the assumption that the external world is unchanging. The second component, the sequence of worlds that the Teller has told the listener are not the actual world, grows by one in each round; this implicitly encodes the assumption that the Teller tells the Listener something in every round. Neither of these are necessary assumptions; I have just made them here for definiteness. Analogous constraints on runs hold if the Listener remembers only the last thing or the last two things that the Teller says.
I have now specified the form of the runs, but this still does not characterize the system. That depends on the Teller's protocol. Consider the following two protocols:
-
The first is probabilistic. In round m < 2n, the Teller chooses a world w′ uniformly at random among the 2n − m world different from the actual world and the (m − 1) worlds that the Listener has already been told about, and the Teller tells the Listener "not w′." After round 2n, the Teller says nothing.
-
The second protocol is deterministic. Order the 2n worlds from (0,…,0) to (1,…, 1) in the obvious way. Let wk be the kth world in this ordering. In round m < 2n, the Teller tells the Listener "not wm" if the actual world is not among the first m worlds; otherwise, the Teller tells the Listener "not wm+1." Again, after round 2n, the Teller says nothing.
If the Listener considers all the initial global states to be equally likely, then it is easy to construct probabilistic systems representing each of these two protocols, for each of the three assumptions made about the Listener's local state. (Note that these constructions implicitly assume that the Teller's protocol is common knowledge: the Listener knows what the protocol is, the Teller knows that the Listener knows, the Listener knows that the Teller knows that the Listener knows, and so on. The construction does not allow for uncertainty about the Teller's protocol, although the framework can certainly model such uncertainty.) Call the resulting systems ![]() i,j ∈ {1, 2}, j ∈ {1, 2, 3} (where i determines which of the two protocols is used and j determines which of the three ways the Listener's state is being modeled). It is easy to see that (1)
i,j ∈ {1, 2}, j ∈ {1, 2, 3} (where i determines which of the two protocols is used and j determines which of the three ways the Listener's state is being modeled). It is easy to see that (1) ![]() 11,
11, ![]() 13,
13, ![]() 21, and
21, and ![]() 23 are synchronous, (2) the Teller has perfect recall in all the systems, and (3) the Listener has perfect recall only in
23 are synchronous, (2) the Teller has perfect recall in all the systems, and (3) the Listener has perfect recall only in ![]() 11 and
11 and ![]() 21 (Exercise 6.11).
21 (Exercise 6.11).
In the system ![]() 11, where the Teller is using the probabilistic protocol and the Listener has perfect recall, the Listener can be viewed as using conditioning at the level of worlds. That is, if the Listener is told "not w"in the mth round, then the set of worlds he considers possible consists of all the worlds he considered possible at time m − 1, other than w. Moreover, the Listener considers each of these worlds equally likely (Exercise 6.12).
11, where the Teller is using the probabilistic protocol and the Listener has perfect recall, the Listener can be viewed as using conditioning at the level of worlds. That is, if the Listener is told "not w"in the mth round, then the set of worlds he considers possible consists of all the worlds he considered possible at time m − 1, other than w. Moreover, the Listener considers each of these worlds equally likely (Exercise 6.12).
In both ![]() 12 and
12 and ![]() 13, conditioning on worlds is not appropriate. Because the Listener forgets everything he has been told (except for the very last thing), the Listener considers possible all worlds other than the one he was just told was impossible. Thus, if w′ is not the world he heard about in the mth round, then he ascribes w′ probability 1/(2n − 1). Note, nevertheless, that conditioning at the level of runs is still used to construct the Listener's probability space in
13, conditioning on worlds is not appropriate. Because the Listener forgets everything he has been told (except for the very last thing), the Listener considers possible all worlds other than the one he was just told was impossible. Thus, if w′ is not the world he heard about in the mth round, then he ascribes w′ probability 1/(2n − 1). Note, nevertheless, that conditioning at the level of runs is still used to construct the Listener's probability space in ![]() 13. Equivalently, the Listener's probability at time m is obtained by conditioning the Listener's initial probability (all the 2n worlds are equally likely) on what he knows at time m (which is just the last thing the Teller told him).
13. Equivalently, the Listener's probability at time m is obtained by conditioning the Listener's initial probability (all the 2n worlds are equally likely) on what he knows at time m (which is just the last thing the Teller told him).
In ![]() 21, even though the Listener has perfect recall, conditioning on worlds is also not appropriate. That is, if the Listener is told "not w" in the mth round, then the set of worlds he considers possible at time m does not necessarily consist of all the worlds he considered possible at time m − 1other than w. In particular, if w = wm +1, then the Listener will know that the actual world is wm. Since he has perfect recall, he will also know it from then on.
21, even though the Listener has perfect recall, conditioning on worlds is also not appropriate. That is, if the Listener is told "not w" in the mth round, then the set of worlds he considers possible at time m does not necessarily consist of all the worlds he considered possible at time m − 1other than w. In particular, if w = wm +1, then the Listener will know that the actual world is wm. Since he has perfect recall, he will also know it from then on.
By way of contrast, in ![]() 22, because the Listener has forgotten everything he has heard, he is in the same position as in
22, because the Listener has forgotten everything he has heard, he is in the same position as in ![]() 12 and
12 and ![]() 13. After hearing "not w," he considers possible all 2n − 1 worlds not other w, and he considers them all equally likely. On the other hand, in
13. After hearing "not w," he considers possible all 2n − 1 worlds not other w, and he considers them all equally likely. On the other hand, in ![]() 23, because he remembers the last two things that the Teller said, if the Listener hears "not wm+1" at time m in run r (rather than "not wm"), then he knows, at the point (r, m), that the actual world is wm. However, he forgets this by time m + 1.
23, because he remembers the last two things that the Teller said, if the Listener hears "not wm+1" at time m in run r (rather than "not wm"), then he knows, at the point (r, m), that the actual world is wm. However, he forgets this by time m + 1.
While this example is quite contrived, it does show that, in general, if an agent starts with a set of possible worlds and learns something about the actual world in each round, then in order for conditioning to be appropriate, not only must perfect recall be assumed, but also that agents learn nothing from what is said beyond the fact that it is true.
6.7.2 The Second-Ace Puzzle
Thinking in terms of protocols also helps in understanding what is going on in the second-ace puzzle from Chapter 1. Recall that in this story, Alice is dealt two cards from a deck of four cards, consisting of the ace and deuce of spades and the ace and deuce of hearts. Alice tells Bob that she has an ace and then tells him that she has the ace of spades. What should the probability be, according to Bob, that Alice has both aces? The calculation done in Chapter 1 gives the answer 1/3. The trouble is that it seems that the probability would also be 1/3 if Alice had said that she had the ace of hearts. It seems unreasonable that Bob's probability that Alice has two aces increases from 1/5 after round 1 to 1/3 after round 2, no matter what ace Alice says she has in round 2.
The first step in analyzing this puzzle in the systems framework is to specify the global states and the exact protocol being used. One reasonable model is to take Alice's local state to consist of the two cards that she was dealt together with the sequence of things she has said and Bob's local state to consist of the sequence things he has heard. (The environment state plays no role here; it can be taken to be the same as Alice's state, just as in the Listener-Teller protocol.)
What about the protocol? One protocol that is consistent with the story is that, initially, Alice is dealt two cards. In the first round, Alice tells Bob whether or not she has an ace. Formally, this means that in a local state where she has an ace, she performs the action of saying "I have an ace"; in a local state where she does not have an ace, she says "I do not have an ace." Then, in round 2, Alice tells Bob she has the ace of spades if she has it and otherwise says she hasn't got it. This protocol is deterministic. There are six possible pairs of cards that Alice could have been dealt, and each one determines a unique run. Since the deal is supposed to be fair, each of these runs has probability 1/6. I leave it to the reader to specify this system formally (Exercise 6.15(a)).
In this system, the analysis of Chapter 1 is perfectly correct. When Alice tells Bob that she has an ace in the first round, then at all time-1 points, Bob can eliminate the run where Alice was not dealt an ace, and his conditional probability that Alice has two aces is indeed 1/5, as suggested in Chapter 1. At time 2, Bob can eliminate two more runs (the runs where Alice does not have the ace of spades), and he assesses the probability that Alice has both aces as 1/3 (Exercise 6.15(b)). Notice, however, that the concern as to what happens if Alice had told Bob that she has the ace of hearts does not arise. This cannot happen, according to the protocol. All that Alice can say is whether or not she has the ace of spades.
Now consider a different protocol (although still one consistent with the story). Again, in round 1, Alice tells Bob whether or not she has an ace. However, now, in round 2, Alice tells Bob which ace she has if she has an ace (and says nothing if she has no ace). This still does not completely specify the protocol. What does Alice tell Bob in round 2 if she has both aces? One possible response is for her to say "I have the ace of hearts" and "I have the ace of spades" with equal probability. This protocol is almost deterministic. The only probabilistic choice occurs if Alice has both aces. With this protocol there are seven runs. Each of the six possible pairs of cards that Alice could have been dealt determines a unique run with the exception of the case where Alice is dealt two aces, for which there are two possible runs (depending on which ace Alice tells Bob she has). Each run has probability 1/6 except for the two runs where Alice was dealt two aces, which each have probability 1/12. Again, I leave it to the reader to model the resulting system formally (Exercise 6.16(a)); it is sketched in Figure 6.7.
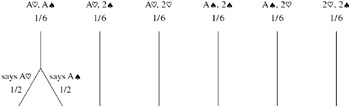
Figure 6.7: A probabilistic protocol for Alice.
It is still the case that at all time-1 points in this system, Bob's conditional probability that Alice has two aces is 1/5. What is the situation at time 2, after Alice says she has the ace of spades? In this case Bob considers three points possible, those in the two runs where Alice has the ace of spades and a deuce, and the point in the run where Alice has both aces and tells Bob she has the ace of spades. Notice, however, that after conditioning, the probability of the point on the run where Alice has both aces is 1/5, while the probability of each of the other two points is 2/5! This is because the probability of the run where Alice holds both aces and tells Bob she has the ace of spades is 1/12, half the probability of the runs where Alice holds only one ace. Thus, Bob's probability that Alice holds both aces at time 2 is 1/5, not 1/3, if this is the protocol. The fact that Alice says she has the ace of spades does not change Bob's assessment of the probability that she has two aces. Similarly, if Alice says that she has the ace of hearts in round 2, the probability that she has two aces remains at 1/5.
The 1/5 here is not the result of Bob conditioning his probability on the initial deal by the information that Alice has the ace of spades (which would result in 1/3, as in the naive analysis in Chapter 1). Naive conditioning is not appropriate here; see the discussion in Section 6.8 and, in particular, Theorem 6.8.1, for a discussion of why this is so.
Now suppose that Alice's protocol is modified so that, if she has both aces, the probability that she says she has the ace of spades is α. Again, there are seven runs. Each of the runs where Alice does not have two aces has probability 1/6. Of the two runs where Alice has both aces, the one where Alice says she has the ace of spades in round 2 has probability α/6; the one where Alice says she the ace of hearts has probability (1 − α)/6. In this case, a similar analysis shows that Bob's probability that Alice holds both aces at time 2 is α/(α + 2) (Exercise 6.16(b)). In the original analysis, α = 1/2, so α/(α + 2) reduces to 1/5. If α = 0, then Alice never says "I have the ace of spades" if she has both aces. In this case, when Bob hears Alice say "I have the ace of spades" in round 2, his probability that Alice has both aces is 0, as expected. If α = 1, which corresponds to Alice saying "I have the ace of spades" either if she has only the ace of spades or if she has both aces, Bob's probability that Alice has both aces is 1/3.
What if Alice does not choose which ace to say probabilistically but uses some deterministic protocol which Bob does not know? In this case, all Bob can say is that the probability that Alice holds both aces is either 0 or 1/3, depending on which protocol Alice is following.
6.7.3 The Monty Hall Puzzle
Last but not least, consider the Monty Hall puzzle. As I observed in Chapter 1, a case can be made that there is no advantage to switching. After all, conditioning says that the car is equally likely to be behind one of the two remaining closed doors. However, another argument says that you ought to switch. You lose by switching if the goat is behind the door you've picked; otherwise, you gain. Since the goat is behind the door you pick initially with probability 2/3 and the car is behind the door with probability 1/3, the probability of gaining by switching is 2/3. Is this argument reasonable? It depends. I'll just sketch the analysis here, since it's so similar to that of the second-ace puzzle.
What protocol describes the situation? Assume that, initially, Monty places a car behind one door and a goat behind the other two. For simplicity, let's assume that the car is equally likely to be placed behind any door. In round 1, you choose a door. In round 2, Monty opens a door (one with a goat behind it other than the one you chose). Finally, in round 3, you must decide if you'll take what's behind your door or what's behind the other unopened door. Again, to completely specify the protocol, it is necessary to say what Monty does if the door you choose has a car behind it (since then he can open either of the other two doors). Suppose that the probability of his opening door j if you choose door i and it has a car behind it is αij (where αii is 0: Monty never opens the door you've chosen). Computations similar to those used for the second-ace puzzle show that, if you initially take door i and Monty then opens door j, the probability of your gaining by switching is 1/(αij + 1) (Exercise 6.17). If αij = 1/2—that is, if Monty is equally likely to open either of the two remaining doors if you choose the door with the car behind it—then the probability of winning if you switch is 2/3, just as in the second argument. If αij = 0, then you are certain that the car cannot be behind the door you opened once Monty opens door j. Not surprisingly, in this case, you certainly should switch; you are certain to win. On the other hand, if αij = 1, you are just as likely to win by switching as by not. Since, with any choice of αij, you are at least as likely to win by switching as by not switching, it seems that you ought to switch.
Is that all there is to it? Actually, it's not quite that simple. This analysis was carried out under the assumption that, in round 2, Monty must open another door. Is this really Monty's protocol? It certainly does not have to be. Suppose that Monty's protocol is such that he opens another door only if the door that you choose has a car behind it (in order to tempt you away from the "good" door). Clearly in this case you should not switch! If Monty opens the door, then you become certain that the door you chose has the car behind it. A more careful analysis of this puzzle must thus consider carefully what Monty's protocol is for opening a door.
The analysis of the three-prisoners puzzle from Example 3.3.1 is, not surprisingly, quite similar to that of the second-ace puzzle and the Monty Hall puzzle. I leave this to the reader (Exercise 6.18).
|
EAN: 2147483647
Pages: 140