6.8 When Conditioning Is Appropriate

Why is it that in the system ₁₁ in Section 6.7.1, the Listener can condition (at the level of worlds) when he hears "not w_m," while in ₂₃ this is not the case? The pat answer is that the Listener gets extra information in ₂₃ because he knows the Teller's protocol. But what is it about the Teller's protocol in ₂₃ that makes it possible for the Listener to get extra information? A good answer to this question should also explain why, in Example 3.1.2, Bob gets extra information from being told that Alice saw the book in the room. It should also help explain why naive conditioning does not work in the second-ace puzzle and the Monty Hall puzzle.

In all of these cases, roughly speaking, there is a naive space and a sophisticated space. For example, in both ₁₁ and ₂₃, the naive space consists of the 2ⁿ possible worlds; the sophisticated spaces are ₁₁ and ₂₃. In the second-ace puzzle, the naive space consists of the six possible pairs of cards that Alice could have. The sophisticated space is the system generated by Alice's protocol; various examples of sophisticated spaces are discussed in Section 6.7.2. Similarly, in the Monty Hall puzzle the naive space consists of three worlds (one for each possible location of the car), and the sophisticated space again depends on Monty's protocol. Implicitly, I have been assuming that conditioning in the sophisticated space always gives the right answer; the question is when conditioning in the naive space gives the same answer.

The naive space is typically smaller and easier to work with than the sophisticated space. Indeed, it is not always obvious what the sophisticated space should be. For example, in the second-ace puzzle, the story does not say what protocol Alice is using, so it does not determine a unique sophisticated space. On the other hand, as these examples show, working in the naive space can often give incorrect answers. Thus, it is important to understand when it is "safe" to condition in the naive space.

Consider the systems ₁₁ and ₂₃ again. It turns out that the reason that conditioning in the naive space is not safe in ₂₃ is that, in ₂₃, the probability of Bob hearing "not w_m" is not the same at all worlds that Bob considers possible at time m − 1. At world w_m it is 1; at all other worlds Bob considers possible it is 0. On the other hand, in ₁₁, Bob is equally likely to hear "not w_m" at all worlds where he could in principle hear "not w_m" (i.e., all worlds other than w_m that have not already been eliminated). Similarly, in Example 3.1.2, Bob is more likely to hear that the book is in the room when the light is on than when the light is off. I now make this precise.

Fix a system and a probability μ on . Suppose that there is a set W of worlds and a map σ from the runs in to W. W is the naive space here, and σ associates with each run a world in the naive space. (Implicitly, I am assuming here that the "world" does not change over time.) In the Listener-Teller example, W consists of the 2ⁿ worlds and σ(r) is the true world in run r. (It is important that the actual world remain unchanged; otherwise, the map σ would not be well defined in this case.) Of course, it is possible that more than one run will be associated with the same world. I focus on agent 1's beliefs about what the world the actual world is. In the Listener-Teller example, the Listener is agent 1. Suppose that at time m in a run of , agent 1's local state has the form ℓo₁,…, o_m〉, where o_i is the agent's ith observation. Taking agent 1's local state to have this form ensures that the system is synchronous for agent 1 and that agent 1 has perfect recall.

For the remainder of this section, assume that the observations o_i are subsets of W and that they are accurate, in that if agent 1 observes U at the point (r, m), then σ(r) ∈ U. Thus, at every round of every run of , agent 1 correctly observes or learns that (σ of) the actual run is in some subset U of W.

This is exactly the setup in the Listener-Teller example (where the sets U have the form W −{w} for some w ∈ W ). It also applies to Example 3.1.2, the second-ace puzzle, the Monty Hall puzzle, and the three-prisoners puzzle from Example 3.3.1. For example, in the Monty Hall Puzzle, if W = {w₁, w₂, w₃}, where w_i is the worlds where the car is behind door i, then when Monty opens door 3, the agent essentially observes {w₁, w₂} (i.e., the car is behind either door 1 or door 2).

Let (, ₁, …) be the unique probability system generated from and μ that satisfies PRIOR. Note that, at each point (r, m), agent 1's probability μ_r, _{m, 1} on the points in ₁(r, m) induces an obvious probability μ^W_{r, m, 1} on W : μ_{r,m, 1}^W(V) = μ_{r,i, 1}({(r′, m) ∈ ₁(r, m) : σ(r′) ∈ V}). The question of whether conditioning is appropriate now becomes whether, on observing U, agent 1 should update his probability on W by conditioning on U. That is, if agent 1's (m + 1)st observation in r is U (i.e., if r₁(m + 1) = r₁(m) U), then is it the case that μ^W_r,_m₊_{1, 1} = μ^W_r,_m_{, 1}( | U)? (For the purposes of this discussion, assume that all sets that are conditioned on are measurable and have positive probability.)

In Section 3.1, I discussed three conditions for conditioning to be appropriate. The assumptions I have made guarantee that the first two hold: agent 1 does not forget and what agent 1 learns/observes is true. That leaves the third condition, that the agent learns nothing from what she observes beyond the fact that it is true. To make this precise, it is helpful to have some notation. Given a local state ℓ = 〈U₁,…, U_m〉 and U ⊆ W, let [ℓ] consist of all runs r where r₁(m) = ℓ, let [U] consist of all runs r such that σ(r) ∈ U, and let ℓ U be the result of appending U to the sequence ℓ. If w ∈ W, I abuse notation and write [w] rather than [{w}]. To simplify the exposition, assume that if ℓ U is a local state in , then [U] and [ℓ] are measurable sets and μ([U] ∩ [ℓ]) > 0, for each set U ⊆ W and local state ℓ in . (Note that this assumption implies that μ([ℓ]) > 0 for each local state ℓ that arises in .) The fact that learning U in local state ℓ gives no more information (about W ) than the fact that U is true then corresponds to the condition that

Intuitively, (6.1) says that in local state ℓ, observing U (which results in local state ℓ U) has the same effect as discovering that U is true, at least as far as the probabilities of subsets of W is concerned.

The following theorem makes precise that (6.1) is exactly what is needed for conditioning to be appropriate:

Theorem 6.8.1

Suppose that r₁(m + 1) = r₁(m) U for r ∈ . The following conditions are equivalent:

if μ^W_r, _{m, 1}(U) > 0, then μ^W_{r, m+}_{1, 1} = μ^W_r_,_m_{, 1}( | U);
if μ(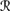[r₁(m) U]) > 0, then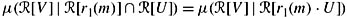

for all V ⊆ W ;
for all w₁, w₂ ∈ U, if μ(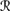[r₁(m)] ∩ 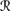[w_i]) > 0 for i = 1, 2, then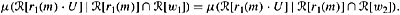
for all w ∈ U such that μ(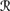[r₁(m)] ∩ 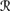[w]) > 0,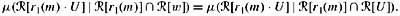
The event 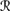[w] is independent of the event 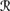[r₁(m) U], given 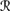[r₁(m)] ∩ 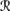[U].

Proof See Exercise 6.13.

Part (a) of Theorem 6.8.1 says that conditioning in the naive space agrees with conditioning in the sophisticated space. Part (b) is just (6.1). Part (c) makes precise the statement that the probability of learning/observing U is the same at all worlds compatible with U that the agent considers possible. The condition that the worlds be compatible with U is enforced by requiring that w₁, w₂ ∈ U; the condition that the agent consider these worlds possible is enforced by requiring that μ([r₁(m)]∩ [w_i]) > 0 for i = 1, 2.

Part (c) of Theorem 6.8.1 gives a relatively straightforward way of checking whether conditioning is appropriate. Notice that in ₁₁, the probability of the Teller saying "not w" is the same at all worlds in _L(r, m) other than w (i.e., it is the same at all worlds in _L(r, m) compatible with what the Listener learns), namely, 1/(2ⁿ − m). This is not the case in ₂₂. If the Listener has not yet figured out what the world is at (r, m), the probability of the Teller saying "not w_m" is the same (namely, 1) at all points in _L(r, m) where the actual world is not w_m. On the other hand, the probability of the Teller saying "not w_m₁" is not the same at all points in _L(r, m) where the actual world is not w_m₊₁. It is 0 at all points in ₁₁ where the actual world is not w^m, but it is 1 at points where the actual world is w_m. Thus, conditioning is appropriate in ₁₁ in all cases; it is also appropriate in ₂₁ at the point (r, m) if the Listener hears "not w_m," but not if the Listener hears "not w_m₊₁."

Theorem 6.8.1 explains why naive conditioning does not work in the second-ace puzzle and the Monty Hall puzzle. In the second-ace puzzle, if Alice tosses a coin to decide what to say if she has both aces, then she is not equally likely to say "I have the ace of spades" at all the worlds that Bob considers possible at time 1 where she in fact has the ace of spades. She is twice as likely to say it if she has the ace of spades and one of the twos as she is if she has both aces. Similarly, if Monty chooses which door to open with equal likelihood if the goat is behind door 1, then he is not equally likely to show door 2 in all cases where the goat is not behind door 2. He is twice is likely to show door 2 if the goat is behind door 3 as he is if the goat is behind door 1.

The question of when conditioning is appropriate goes far beyond these puzzles. It turns out that to be highly relevant in the statistical areas of selectively reported data and missing data. For example, consider a questionnaire where some people answer only some questions. Suppose that, of 1,000 questionnaires returned, question 6 is answered "yes" in 300, "no" in 600, and omitted in the remaining 100. Assuming people answer truthfully (clearly not always an appropriate assumption!), is it reasonable to assume that in the general population, 1/3 would answer "yes" to question 6 and 2/3 would answer "no"? This is reasonable if the data is "missing at random," so that people who would have said "yes" are equally likely not to answer the question as people who would have said "no." However, consider a question such as "Have you ever shoplifted?" Are shoplifters really just as likely to answer that question as nonshoplifters?

This issue becomes particularly significant when interpreting census data. Some people are invariably missed in gathering census data. Are these people "missing at random"? Almost certainly not. For example, homeless people and people without telephones are far more likely to be underrepresented, and this underrepresentation may skew the data in significant ways.