6.5 Markovian Systems

Although assuming a prior probability over runs helps explain where the probability measure at each point is coming from, runs are still infinite objects and a system may have infinitely many of them. Indeed, even in systems where there are only two global states, there may be uncountably many runs. (Consider a system where a coin is tossed infinitely often and the global state describes the outcome of the last coin toss.) Where is the probability on runs coming from? Is there a compact way of describing and representing it?

In many cases it is possible to assign a probability to the transition from one state to another. Consider the two-coin example described in Figure 6.4. Because the first coin has a probability 2/3 of landing heads, the transition from the initial state to the state where it lands heads has probability 2/3; this is denoted by labeling the left edge coming from the root by 2/3 in Figure 6.4. Similarly, the right edge is labeled by 1/3 to denote that the probability of making the transition to the state where the coin lands heads is 1/3. All the other edges are labeled by 1/2, since the probability of each transition resulting from tossing the second (fair) coin is 1/2. Because the coin tosses are assumed independent and there is a single initial state, the probability of a run in this system can be calculated by multiplying the probabilities labeling its edges.

This type of calculation is quite standard and is abstracted in the notion of a Markovian system. In Markovian systems, appropriate independence assumptions are made that allow the prior probability on runs to be generated from a probability on state transitions.

To make this precise, let be a system whose global states come from a set Σ. For m = 0, 1, 2, …, let G_m be a random variable on such that G_m(r) = r(m)—that is, G_m maps r to the global state in r at time m. A time-m event is a Boolean combination of events of the form G_i = g for i ≤ m. Of particular interest are time-m events of the form (G₀ = g₀) ∩ … ∩ (G_m = g_m), which is abbreviated as [g₀,…, g_m]; this is the set of all runs in with initial prefix g₀,…, g_m. Such an event is called an m-prefix. As the name suggests, this is the event consisting of all runs whose first m + 1 global states are g₀,…, g_m. It is easy to show that every time-m event U is a union of m-prefixes; moreover, the set _pref, which consists of the time-m events for all m, is an algebra (Exercise 6.9).

Definition 6.5.1

A probability measure μ on the algebra _pref is Markovian if, for all m, m′ ≥ 0,

(G_m₊₁ = g′ | G_m = g) = (G_m′₊₁ = g′ | G_m′ = g); and
(G_m₊₁ = g′ | U ∩ G_m = g) = (G_m₊₁ = g′ | G_m = g), where U is a time-m event in .

The first requirement essentially says that, for each pair (g, g′) of global states, there is a well-defined transition probability—the probability of making the transition from g to g′ —that does not depend on the time of the transition. The second requirement says the probability that the (m + 1)st global state in a run g′ is independent of preceding global states given the value of the mth global state. Put another way, the probability of making a transition from global state g at time m to g′ at time m + 1 is independent of how the system reached global state g.

The main interest in Markovian probability measures on systems is not that they admit well-defined transition probabilities, but that, starting with the transition probabilities and a prior on initial states, a unique Markovian probability measure on runs can be defined. Define a transition probability function τ to be a mapping from pairs of global state g, g′ to [0, 1]such that ∑_{g′ ∈Σ} τ(g, g′) = 1 for each g ∈ Σ. The requirement that the transition probabilities from a fixed g must sum to 1 just says that the sum of the probabilities over all possible transitions from g must be 1.

Proposition 6.5.2

Given a transition probability function τ and a prior μ₀ on 0 - prefixes, there is a unique Markovian probability measure μ on _pref such that μ(G_n+1 = g′ | G_n = g) = τ(g, g′) and μ([g₀]) = μ₀([g₀]).

Proof Since _pref consists of time-m events (for all m) and, by Exercise 6.9(a), every time-m event can be written as the disjoint union of m-prefixes, it suffices to show that μ is uniquely defined on m-prefixes. This is done by induction on m. If m = 0, then clearly ([g₀]) = μ₀([g₀]). For the inductive step, assume that m > 0 and that μ has been defined on all (m − 1)-prefixes. Then

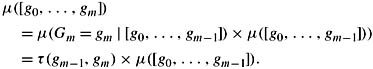
Thus, μ is uniquely defined on m-prefixes. Moreover, an easy induction argument now shows that

It is easy to check that μ is in fact Markovian and is the unique probability measure on _pref such that μ(G_n₊₁ = g′ | G_n = g) = τ(g, g′) and μ([g₀]) = μ₀([g₀]) (Exercise 6.10).