6.6 REPRESENTING THREE-ADDRESS STATEMENTS
6.5 INTERMEDIATE CODE GENERATION
While translating a source program into a functionally equivalent object code representation, a parser may first generate an intermediate representation. This makes retargeting of the code possible and allows some optimizations to be carried out that would otherwise not be possible. The following are commonly used intermediate representations:
-
Postfix notation
-
Syntax tree
-
Three-address code
Postfix Notation
In postfix notation, the operator follows the operand. For example, in the expression ( a ˆ’ b ) * ( c + d ) + ( a ˆ’ b ), the postfix representation is:
Syntax Tree
The syntax tree is nothing more than a condensed form of the parse tree. The operator and keyword nodes of the parse tree (Figure 6.5) are moved to their parent, and a chain of single productions is replaced by single link (Figure 6.6).
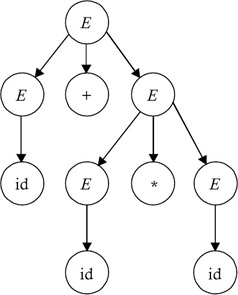
Figure 6.5: Parse tree for the string id+id*id.
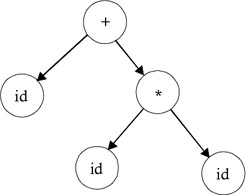
Figure 6.6: Syntax tree for id+id*id.
Three-Address Code
Three address code is a sequence of statements of the form x = y op z . Since a statement involves no more than three references, it is called a "three-address statement," and a sequence of such statements is referred to as three-address code. For example, the three-address code for the expression a + b * c + d is:
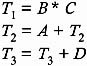
Sometimes a statement might contain less than three references; but it is still called a three-address statement. The following are the three-address statements used to represent various programming language constructs:
-
Used for representing arithmetic expressions:
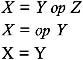
-
Used for representing Boolean expressions:

-
Used for representing array references and dereferencing operations:
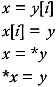
-
Used for representing a procedure call:
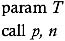
EAN: 2147483647
Pages: 108
- Structures, Processes and Relational Mechanisms for IT Governance
- An Emerging Strategy for E-Business IT Governance
- Linking the IT Balanced Scorecard to the Business Objectives at a Major Canadian Financial Group
- Technical Issues Related to IT Governance Tactics: Product Metrics, Measurements and Process Control
- Managing IT Functions