9.2 Multiprecision Operations

9.2 Multiprecision Operations

One big advantage of assembly language over high level languages is that assembly language does not limit the size of integer operations. For example, the standard C programming language defines three different integer sizes: short int, int, and long int.^[1] On the PC, these are often 16- and 32-bit integers. Although the 80x86 machine instructions limit you to processing 8-, 16-, or 32-bit integers with a single instruction, you can always use more than one instruction to process integers of any size you desire. If you want to add 256-bit integer values together, no problem; it's relatively easy to accomplish this in assembly language. The following sections describe how extended various arithmetic and logical operations from 16 or 32 bits to as many bits as you please.

9.2.1 HLA Standard Library Support for Extended Precision Operations

Although it is important for you to understand how to do extended precision arithmetic yourself, you should note that the HLA Standard Library provides a full set of 64-bit and 128-bit arithmetic and logical functions that you can use. These routines are very general purpose and are very convenient to use. This section will briefly describe the HLA Standard Library support for extended precision arithmetic.

As noted in earlier chapters, the HLA compiler supports several different 64-bit and 128-bit data types. As a review, here are the extended data types that HLA supports:

• uns64: 64-bit unsigned integers

• int64: 64-bit signed integers

• qword: 64-bit untyped values

• uns128: 128-bit unsigned integers

• int128: 128-bit signed integers

• lword: 128-bit untyped values

HLA also provides a tbyte type, but we will not consider that here (see the section on decimal arithmetic later in this chapter).

HLA lets you create constants, types, and variables whose type is one of the above. HLA fully supports 64-bit and 128-bit literal constants and constant arithmetic. This allows you to initialize 64- and 128-bit static objects using standard decimal, hexadecimal, or binary notation. For example:

 static      u128 :uns128 := 123456789012345678901233567890;      i64  :int64 := -12345678901234567890;      lw   :lword := $1234_5678_90ab_cdef_0000_ffff; 

Of course, the 80x86 general purpose integer registers don't support 64-bit or 128-bit operands, so you may not directly manipulate these values with single 80x86 machine instructions (though you'll see how to do this with multiple instructions starting in the next section).

In order to easily manipulate 64-bit and 128-bit values, the HLA Standard Library's math.hhf module provides a set of functions that handle most of the standard arithmetic and logical operations you'll need. You use these functions in a manner quite similar to the standard 32-bit arithmetic and logical instructions. For example, consider the math.addq (qword) and math.addl (lword) functions:

      math.addq( left64, right64, dest64 );      math.addl( left128, right128, dest128 ); 

These functions compute the following:

 dest64 := left64 + right64;    // dest64, left64, and right64                                // must be 8-byte operands dest128 := left128 + right128; // dest128, left128, and right128                                // must be 16-byte operands 

These functions also leave all the 80x86 flags set the same way you'd expect them after the execution of an add instruction. Specifically, these functions set the zero flag if the (full) result is zero, they set the carry flag if there is a carry out of the H.O. bit, they set the overflow flag if there is a signed overflow, and they set the sign flag if the H.O. bit of the result contains one.

Most of the remaining arithmetic and logical routines use the same calling sequence as math.addq and math.addl. Briefly, here are the functions that use the same syntax:

    math.andq( left64, right64, dest64 );    math.andl( left128, right128, dest128 );    math.divq( left64, right64, dest64 );    math.divl( left128, right128, dest128 );    math.idivq( left64, right64, dest64 );    math.idivl( left128, right128, dest128 );    math.modq( left64, right64, dest64 );    math.modl( left128, right128, dest128 );    math.imodq( left64, right64, dest64 );    math.imodl( left128, right128, dest128 );    math.mulq( left64, right64, dest64 );    math.mull( left128, right128, dest128 );    math.imulq( left64, right64, dest64 );    math.imull( left128, right128, dest128 );    math.orq( left64, right64, dest64 );    math.orl( left128, right128, dest128 );    math.subq( left64, right64, dest64 );    math.subl( left128, right128, dest128 );    math.xorq( left64, right64, dest64 );    math.xorl( left128, right128, dest128 ); 

These functions set the flags the same way as the corresponding 32-bit machine instructions and, in the case of the divide and modulo functions, raise the same exceptions. Note that the multiplication functions do not produce an extended precision result. The destination value is the same size as the source operands. These functions set the overflow and carry flags if the result does not fit into the destination operand. All of these functions compute the following:

 dest64 := left64 op right64; dest128 := left128 op right128; 

where op represents the specific operation.

In addition to the above functions, the HLA Standard Library's math module also provides a few additional functions whose syntax is slightly different. This list includes math.negq, math.negl, math.notq, math.notl, math.shlq, math.shll, math.shrq, and math.shrl. Note that there are no rotates or arithmetic shift right functions. However, you'll soon see that these operations are easy to synthesize using standard instructions. Here are the prototypes for these additional functions:

 math.negq( source:qword; var dest:qword ); math.negl( source:lword; var dest:lword ); math.notq( source:qword; var dest:qword ); math.notl( source:lword; var dest:lword ); math.shlq( count:uns32; source:qword; var dest:qword ); math.shll( count:uns32; source:lword; var dest:lword ); math.shrq( count:uns32; source:qword; var dest:qword ); math.shrl( count:uns32; source:lword; var dest:lword ); 

Again, all these functions set the flags exactly the same way the corresponding machine instructions would set the flags were they to support 64-bit or 128-bit operands.

The HLA Standard Library also provides a full complement of I/O and conversion routines for 64-bit and 128-bit values. For example, you can use stdout.put to display 64- and 128-bit values, you may use stdin.get to read these values, and there are a set of routines in the HLA conversions module that convert between these values and their string equivalents. In general, anything you can do with a 32-bit value can be done with a 64-bit or 128-bit value as well. See the HLA Standard Library documentation for more details.

9.2.2 Multiprecision Addition Operations

The 80x86 add instruction adds two 8-, 16-, or 32-bit numbers. After the execution of the add instruction, the 80x86 carry flag is set if there is an overflow out of the H.O. bit of the sum. You can use this information to do multiprecision addition operations. Consider the way you manually perform a multidigit (multiprecision) addition operation:

 Step 1: Add the least significant digits together:         289                  289        +456 produces        +456         ----                 ----                                5 with carry 1. Step 2: Add the next significant digits plus the carry:         1 (previous carry)         289                  289        +456 produces        +456         ----                 ----           5                   45 with carry 1. Step 3: Add the most significant digits plus the carry:                                 1 (previous carry)            289                  289           +456 produces        +456            ----                 ----             45                  745 

The 80x86 handles extended precision arithmetic in an identical fashion, except instead of adding the numbers a digit at a time, it adds them together a byte, word, or double word at a time. Consider the three double word (96-bit) addition operation in Figure 9-1 on the following page.

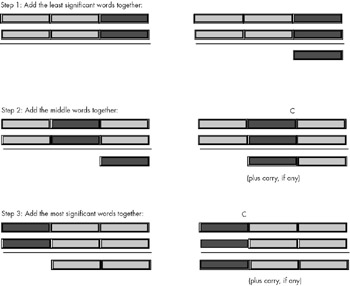
Figure 9-1: Adding Two 96-Bit Objects Together.

As you can see from this figure, the idea is to break up a larger operation into a sequence of smaller operations. Because the x86 processor family is capable of adding together, at most, 32 bits at a time, the operation must proceed in blocks of 32 bits or less. So the first step is to add the two L.O. double words together just as we would add the two L.O. digits of a decimal number together in the manual algorithm. There is nothing special about this operation; you can use the add instruction to achieve this.

The second step involves adding together the second pair of double words in the two 96-bit values. Note that in step two, the calculation must also add in the carry out of the previous addition (if any). If there was a carry out of the L.O. addition, the add instruction sets the carry flag to one; conversely, if there was no carry out of the L.O. addition, the earlier add instruction clears the carry flag. Therefore, in this second addition, we really need to compute the sum of the two double words plus the carry out of the first instruction. Fortunately, the x86 CPUs provide an instruction that does exactly this: the adc (add with carry) instruction. The adc instruction uses the same syntax as the add instruction and performs almost the same operation:

 adc( source, dest ); // dest := dest + source + C 

As you can see, the only difference between the add and adc instruction is that the adc instruction adds in the value of the carry flag along with the source and destination operands. It also sets the flags the same way the add instruction does (including setting the carry flag if there is an unsigned overflow). This is exactly what we need to add together the middle two double words of our 96-bit sum.

In step three of Figure 9-1, the algorithm adds together the H.O. double words of the 96-bit value. This addition operation must also incorporate the carry out of the sum of the middle two double words; hence the adc instruction is needed here, as well. To sum it up, the add instruction adds the L.O. double words together. The adc (add with carry) instruction adds all other double word pairs together. At the end of the extended precision addition sequence, the carry flag indicates unsigned overflow (if set), a set overflow flag indicates signed overflow, and the sign flag indicates the sign of the result. The zero flag doesn't have any real meaning at the end of the extended precision addition (it simply means that the sum of the H.O. two double words is zero and does not indicate that the whole result is zero); if you want to see how to check for an extended precision zero result, see the source code for the HLA Standard Library math.addq or math.addl function.

For example, suppose that you have two 64-bit values you wish to add together, defined as follows:

 static      X: qword;      Y: qword; 

Suppose also that you want to store the sum in a third variable, Z, which is also a qword. The following 80x86 code will accomplish this task:

    mov( (type dword X), eax );          // Add together the L.O. 32 bits    add( (type dword Y), eax );          // of the numbers and store the    mov( eax, (type dword Z) );          // result into the L.O. dword of Z.    mov( (type dword X[4]), eax );       // Add together (with carry) the    adc( (type dword Y[4]), eax );       // H.O. 32 bits and store the result    mov( eax, (type dword Z[4]) );       // into the H.O. dword of Z. 

Remember, these variables are qword objects. Therefore the compiler will not accept an instruction of the form "mov( X, eax );" because this instruction would attempt to load a 64-bit value into a 32-bit register. This code uses the coercion operator to coerce symbols X, Y, and Z to 32 bits. The first three instructions add the L.O. double words of X and Y together and store the result at the L.O. double word of Z. The last three instructions add the H.O. double words of X and Y together, along with the carry out of the L.O. word, and store the result in the H.O. double word of Z. Remember, address expressions of the form "X[4]" access the H.O. double word of a 64-bit entity. This is due to the fact that the x86 memory space addresses bytes, and it takes four consecutive bytes to form a double word.

You can extend this to any number of bits by using the adc instruction to add in the higher order values. For example, to add together two 128-bit values, you could use code that looks something like the following:

 type      tBig: dword[4]; // Storage for four dwords is 128 bits. static      BigVal1: tBig;      BigVal2: tBig;      BigVal3: tBig;      .      .    mov( BigVal1[0], eax ); // Note there is no need for (type dword BigValx)    add( BigVal2[0], eax ); // because the base type of BitValx is dword.    mov( eax, BigVal3[0] );    mov( BigVal1[4], eax );    adc( BigVal2[4], eax );    mov( eax, BigVal3[4] );    mov( BigVal1[8], eax );    adc( BigVal2[8], eax );    mov( eax, BigVal3[8] );    mov( BigVal1[12], eax );    adc( BigVal2[12], eax );    mov( eax, BigVal3[12] ); 

9.2.3 Multiprecision Subtraction Operations

Like addition, the 80x86 performs multibyte subtraction the same way you would manually, except it subtracts whole bytes, words, or double words at a time rather than decimal digits. The mechanism is similar to that for the add operation. You use the sub instruction on the L.O. byte/word/double word and sbb (subtract with borrow) instruction on the high order values. The following example demonstrates a 64-bit subtraction using the 32-bit registers on the 80x86:

 static      Left:   qword;      Right:  qword;      Diff:   qword;            .            .            .      mov( (type dword Left), eax );      sub( (type dword Right), eax );      mov( eax, (type dword Diff) );      mov( (type dword Left[4]), eax );      sbb( (type dword Right[4]), eax );      mov( (type dword Diff[4]), eax ); 

The following example demonstrates a 128-bit subtraction:

 type      tBig: dword[4]; // Storage for four dwords is 128 bits. static      BigVal1: tBig;      BigVal2: tBig;      BigVal3: tBig;       .       .       .      // Compute BigVal3 := BigVal1 - BigVal2      mov( BigVal1[0], eax ); // Note there is no need for (type dword BigValx)      sub( BigVal2[0], eax ); // because the base type of BitValx is dword.      mov( eax, BigVal3[0] );      mov( BigVal1[4], eax );      sbb( BigVal2[4], eax );      mov( eax, BigVal3[4] );      mov( BigVal1[8], eax );      sbb( BigVal2[8], eax );      mov( eax, BigVal3[8] );      mov( BigVal1[12], eax );      sbb( BigVal2[12], eax );      mov( eax, BigVal3[12] ); 

9.2.4 Extended Precision Comparisons

Unfortunately, there isn't a "compare with borrow" instruction that you can use to perform extended precision comparisons. Because the cmp and sub instructions perform the same operation, at least as far as the flags are concerned, you'd probably guess that you could use the sbb instruction to synthesize an extended precision comparison; however, you'd only be partly right. There is, however, a better way, so there is no need to explore the use of sbb for extended precision comparison.

Consider the two unsigned values $2157 and $1293. The L.O. bytes of these two values do not affect the outcome of the comparison. Simply comparing the H.O. bytes, $21 with $12, tells us that the first value is greater than the second. In fact, the only time you ever need to look at both bytes of these values is if the H.O. bytes are equal. In all other cases comparing the H.O. bytes tells you everything you need to know about the values. Of course, this is true for any number of bytes, not just two. The following code compares two signed 64-bit integers by comparing their H.O. double words first and comparing their L.O. double words only if the H.O. double words are equal:

 // This sequence transfers control to location "IsGreater" if // QwordValue > QwordValue2. It transfers control to "IsLess" if // QwordValue < QwordValue2. It falls though to the instruction // following this sequence if QwordValue = QwordValue2. To test for // inequality, change the "IsGreater" and "IsLess" operands to "NotEqual" // in this code.          mov( (type dword QWordValue[4]), eax ); // Get H.O. dword          cmp( eax, (type dword QWordValue2[4]));          jg IsGreater;          jl IsLess;          mov( (type dword QWordValue[0]), eax ); // If H.O. dwords were equal,          cmp( eax, (type dword QWordValue2[0])); // then we must compare the          jg IsGreater; // L.O. dwords.          jl IsLess; // Fall through to this point if the two values were equal. 

To compare unsigned values, simply use the ja and jb instructions in place of jg and jl.

You can easily synthesize any possible comparison from the preceding sequence. The following examples show how to do this. These examples demonstrate signed comparisons; just substitute ja, jae, jb, and jbe for jg, jge, jl, and jle (respectively) if you want unsigned comparisons.

 static      QW1: qword;      QW2: qword; const      QW1d: text := "(type dword QW1)";      QW2d: text := "(type dword QW2)"; // 64-bit test to see if QW1 < QW2 (signed). // Control transfers to "IsLess" label if QW1 < QW2. Control falls // through to the next statement if this is not true.      mov( QW1d[4], eax ); // Get H.O. dword      cmp( eax, QW2d[4] );      jg NotLess;      jl IsLess;      mov( QW1d[0], eax ); // Fall through to here if the H.O. dwords are equal.      cmp( eax, QW2d[0] );      jl IsLess; NotLess: // 64-bit test to see if QW1 <= QW2 (signed). Jumps to "IsLessEq" if the // condition is true.      mov( QW1d[4], eax ); // Get H.O. dword      cmp( eax, QW2d[4] );      jg NotLessEQ;      jl IsLessEQ;      mov( QW1d[0], eax ); // Fall through to here if the H.O. dwords are equal.      cmp( eax, QW2d[0] );      jle IsLessEQ; NotLessEQ: // 64-bit test to see if QW1 > QW2 (signed). Jumps to "IsGtr" if this condition // is true.      mov( QW1d[4], eax ); // Get H.O. dword      cmp( eax, QW2d[4] );      jg IsGtr;      jl NotGtr;      mov( QW1d[0], eax ); // Fall through to here if the H.O. dwords are equal.      cmp( eax, QW2d[0] );      jg IsGtr; NotGtr: // 64-bit test to see if QW1 >= QW2 (signed). Jumps to "IsGtrEQ" if this // is the case.      mov( QW1d[4], eax ); // Get H.O. dword      cmp( eax, QW2d[4] );      jg IsGtrEQ;      jl NotGtrEQ;      mov( QW1d[0], eax ); // Fall through to here if the H.O. dwords are equal.      cmp( eax, QW2d[0] );      jge IsGtrEQ; NotGtrEQ: // 64-bit test to see if QW1 = QW2 (signed or unsigned). This code branches // to the label "IsEqual" if QW1 = QW2. It falls through to the next instruction // if they are not equal.      mov( QW1d[4], eax ); // Get H.O. dword      cmp( eax, QW2d[4] );      jne NotEqual;      mov( QW1d[0], eax ); // Fall through to here if the H.O. dwords are equal.      cmp( eax, QW2d[0] );      je IsEqual; NotEqual: // 64-bit test to see if QW1 <> QW2 (signed or unsigned). This code branches // to the label "NotEqual" if QW1 <> QW2. It falls through to the next // instruction if they are equal.      mov( QW1d[4], eax ); // Get H.O. dword      cmp( eax, QW2d[4] );      jne NotEqual;      mov( QW1d[0], eax ); // Fall through to here if the H.O. dwords are equal.      cmp( eax, QW2d[0] );      jne NotEqual; // Fall through to this point if they are equal. 

You cannot directly use the HLA high level control structures if you need to perform an extended precision comparison. However, you may use the HLA hybrid control structures and bury the appropriate comparison into this statement. Doing so will probably make your code easier to read. For example, the following if..then..else..endif statement checks to see if QW1 > QW2 using a 64-bit extended precision unsigned comparison:

 if ( #{     mov( QW1d[4], eax );     cmp( eax, QW2d[4] );     jg true;     mov( QW1d[0], eax );     cmp( eax, QW2d[0] );     jng false; }# ) then     << code to execute if QW1 > QW2 >> else     << code to execute if QW1 <= QW2 >> endif; 

If you need to compare objects that are larger than 64 bits, it is very easy to generalize the preceding code for 64-bit operands. Always start the comparison with the H.O. double words of the objects and work you way down toward the L.O. double words of the objects as long as the corresponding double words are equal. The following example compares two 128-bit values to see if the first is less than or equal (unsigned) to the second:

 static      Big1: uns128;      Big2: uns128;       .       .       .      if      ( #{          mov( Big1[12], eax );          cmp( eax, Big2[12] );          jb true;          jg false;          mov( Big1[8], eax );          cmp( eax, Big2[8] );          jb true;          jg false;          mov( Big1[4], eax );          cmp( eax, Big2[4] );          jb true;          jg false;          mov( Big1[0], eax );          cmp( eax, Big2[0] );          jnbe false;      }# ) then          << Code to execute if Big1 <= Big2 >> else          << Code to execute if Big1 > Big2 >> endif; 

9.2.5 Extended Precision Multiplication

Although an 8x8, 16x16, or 32x32 multiply is usually sufficient, there are times when you may want to multiply larger values together. You will use the x86 single operand mul and imul instructions for extended precision multiplication.

Not surprisingly (in view of how we achieved extended precision addition using adc and sbb), you use the same techniques to perform extended precision multiplication on the 80x86 that you employ when manually multiplying two values. Consider a simplified form of the way you perform multidigit multiplication by hand:

 1) Multiply the first two     2) Multiply 5*2:    digits together (5*3):    123                              123     45                               45    ---                              ---     15                               15                                     10 3) Multiply 5*1:              4) Multiply 4*3:    123                              123     45                               45    ---                              ---     15                               15    10                               10    5                                5                                     12 5) Multiply 4*2:              6) Multiply 4*1:    123                              123     45                               45    ---                              ---     15                               15    10                               10    5                                5    12                               12    8                                8                                    4 7) Add all the partial products together:    123     45    ---     15    10    5    12    8   4   ------   5535 

The 80x86 does extended precision multiplication in the same manner except that it works with bytes, words, and double words rather than digits. Figure 9-2 shows how this works.

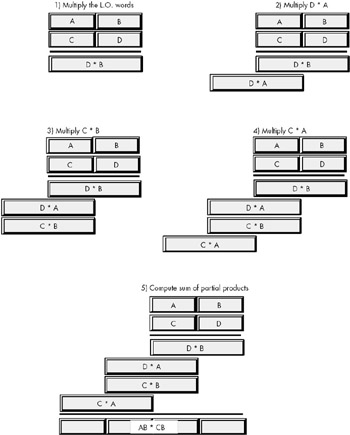
Figure 9-2: Extended Precision Multiplication.

Probably the most important thing to remember when performing an extended precision multiplication is that you must also perform a multiple precision addition at the same time. Adding up all the partial products requires several additions that will produce the result. Listing 9-1 demonstrates the proper way to multiply two 64-bit values on a 32-bit processor:

Listing 9-1: Extended Precision Multiplication.

 program testMUL64; #include( "stdlib.hhf" ) procedure MUL64( Multiplier:qword; Multiplicand:qword; var Product:lword ); const      mp: text := "(type dword Multiplier)";      mc: text := "(type dword Multiplicand)";      prd:text := "(type dword [edi])"; begin MUL64;      mov( Product, edi );      // Multiply the L.O. dword of Multiplier times Multiplicand.      mov( mp, eax );      mul( mc, eax );    // Multiply L.O. dwords.      mov( eax, prd );   // Save L.O. dword of product.      mov( edx, ecx );   // Save H.O. dword of partial product result.      mov( mp, eax );      mul( mc[4], eax ); // Multiply mp(L.O.) * mc(H.O.)      add( ecx, eax );   // Add to the partial product.      adc( 0, edx );     // Don't forget the carry!      mov( eax, ebx );   // Save partial product for now.      mov( edx, ecx );      // Multiply the H.O. word of Multiplier with Multiplicand.      mov( mp[4], eax ); // Get H.O. dword of Multiplier.      mul( mc, eax );    // Multiply by L.O. word of Multiplicand.      add( ebx, eax );   // Add to the partial product.      mov( eax, prd[4] );// Save the partial product.      adc( edx, ecx );   // Add in the carry!      mov( mp[4], eax ); // Multiply the two H.O. dwords together.      mul( mc[4], eax );      add( ecx, eax );   // Add in partial product.      adc( 0, edx );     // Don't forget the carry!      mov( eax, prd[8] );// Save the partial product.      mov( edx, prd[12] ); end MUL64; static      op1: qword;      op2: qword;      rslt: lword; begin testMUL64;      // Initialize the qword values (note that static objects      // are initialized with zero bits).      mov( 1234, (type dword op1 ));      mov( 5678, (type dword op2 ));      MUL64( op1, op2, rslt );      // The following only prints the L.O. qword, but      // we know the H.O. qword is zero so this is okay.      stdout.put( "rslt=" );      stdout.putu64( (type qword rslt)); end testMUL64; 

One thing you must keep in mind concerning this code is that it only works for unsigned operands. To multiply two signed values you must note the signs of the operands before the multiplication, take the absolute value of the two operands, do an unsigned multiplication, and then adjust the sign of the resulting product based on the signs of the original operands. Multiplication of signed operands is left as an exercise to the reader (or you could just check out the source code in the HLA Standard Library).

The example in Listing 9-1 was fairly straight-forward because it was possible to keep the partial products in various registers. If you need to multiply larger values together, you will need to maintain the partial products in temporary (memory) variables. Other than that, the algorithm that Listing 9-1 uses generalizes to any number of double words.

9.2.6 Extended Precision Division

You cannot synthesize a general n-bit/m-bit division operation using the div and idiv instructions. You must perform such operations using a sequence of shift and subtract instructions, and it is extremely messy. However, a less general operation, dividing an n-bit quantity by a 32-bit quantity is easily synthesized using the div instruction. This section presents both methods for extended precision division.

Before describing how to perform a multiprecision division operation, you should note that some operations require an extended precision division even though they may look calculable with a single div or idiv instruction. Dividing a 64-bit quantity by a 32-bit quantity is easy, as long as the resulting quotient fits into 32 bits. The div and idiv instructions will handle this directly. However, if the quotient does not fit into 32 bits then you have to handle this problem as an extended precision division. The trick here is to divide the (zero or sign extended) H.O double word of the dividend by the divisor, and then repeat the process with the remainder and the L.O. dword of the dividend. The following sequence demonstrates this:

 static      dividend: dword[2] := [$1234, 4]; // = $4_0000_1234.      divisor: dword := 2;              // dividend/divisor = $2_0000_091A      quotient: dword[2];      remainder:dword;       .       .       .      mov( divisor, ebx );      mov( dividend[4], eax );      xor( edx, edx );         // Zero extend for unsigned division.      div( ebx, edx:eax );      mov( eax, quotient[4] ); // Save H.O. dword of the quotient (2).      mov( dividend[0], eax ); // Note that this code does *NOT* zero extend      div( ebx, edx:eax );     // EAX into EDX before this DIV instr.      mov( eax, quotient[0] ); // Save L.O. dword of the quotient ($91a).      mov( edx, remainder );   // Save away the remainder. 

Because it is perfectly legal to divide a value by one, it is certainly possible that the resulting quotient after a division could require as many bits as the dividend. That is why the quotient variable in this example is the same size (64 bits) as the dividend variable (note the use of an array of two double words rather than a qword type; this spares the code from having to coerce the operands to double words). Regardless of the size of the dividend and divisor operands, the remainder is always no larger than the size of the division operation (32 bits in this case). Hence the remainder variable in this example is just a double word.

Before analyzing this code to see how it works, let's take a brief look at why a single 64/32 division will not work for this particular example even though the div instruction does indeed calculate the result for a 64/32 division. The naive approach, assuming that the x86 were capable of this operation, would look something like the following:

      // This code does *NOT* work!      mov( dividend[0], eax ); // Get dividend into edx:eax      mov( divident[4], edx );      div( divisor, edx:eax ); // Divide edx:eax by divisor. 

Although this code is syntactically correct and will compile, if you attempt to run this code it will raise an ex.DivideError^[2] exception. The reason, if you'll remember how the div instruction works, is that the quotient must fit into 32 bits; because the quotient turns out to be $2_0000_091A, it will not fit into the EAX register, hence the resulting exception.

Now let's take another look at the former code that correctly computes the 64/32 quotient. This code begins by computing the 32/32 quotient of dividend[4]/divisor. The quotient from this division (2) becomes the H.O. double word of the final quotient. The remainder from this division (0) becomes the extension in EDX for the second half of the division operation. The second half of the code divides edx:dividend[0] by divisor to produce the L.O. double word of the quotient and the remainder from the division. Note that the code does not zero extend EAX into EDX prior to the second div instruction. EDX already contains valid bits, and this code must not disturb them.

The 64/32 division operation above is actually just a special case of the more general division operation that lets you divide an arbitrary-sized value by a 32-bit divisor. To achieve this, you begin by moving the H.O. double word of the dividend into EAX and zero extending this into EDX. Next, you divide this value by the divisor. Then, without modifying EDX along the way, you store away the partial quotients, load EAX with the next lower double word in the dividend, and divide it by the divisor. You repeat this operation until you've processed all the double words in the dividend. At that time the EDX register will contain the remainder. The program in Listing 9-2 demonstrates how to divide a 128-bit quantity by a 32-bit divisor, producing a 128-bit quotient and a 32-bit remainder.

Listing 9-2: Unsigned 128/32-Bit Extended Precision Division.

 program testDiv128; #include( "stdlib.hhf" ) procedure div128 (         Dividend: lword;         Divisor: dword;     var QuotAdrs: lword;     var Remainder: dword );  @nodisplay; const    Quotient: text := "(type dword [edi])"; begin div128;    push( eax );    push( edx );    push( edi );    mov( QuotAdrs, edi );     // Pointer to quotient storage.    mov( Dividend[12], eax ); // Begin division with the H.O. dword.    xor( edx, edx );          // Zero extend into EDX.    div( Divisor, edx:eax );  // Divide H.O. dword.    mov( eax, Quotient[12] ); // Store away H.O. dword of quotient.    mov( Dividend[8], eax );  // Get dword #2 from the dividend    div( Divisor, edx:eax );  // Continue the division.    mov( eax, Quotient[8] );  // Store away dword #2 of the quotient.    mov( Dividend[4], eax );  // Get dword #1 from the dividend.    div( Divisor, edx:eax );  // Continue the division.    mov( eax, Quotient[4] );  // Store away dword #1 of the quotient.    mov( Dividend[0], eax );  // Get the L.O. dword of the dividend.    div( Divisor, edx:eax );  // Finish the division.    mov( eax, Quotient[0] );  // Store away the L.O. dword of the quotient.    mov( Remainder, edi );    // Get the pointer to the remainder's value.    mov( edx, [edi] );        // Store away the remainder value.    pop( edi );    pop( edx );    pop( eax ); end div128; static      op1: lword := $8888_8888_6666_6666_4444_4444_2222_2221;      op2: dword := 2;      quo: lword;      rmndr: dword; begin testDiv128;    div128( op1, op2, quo, rmndr );    stdout.put    (       nl       nl       "After the division: " nl       nl       "Quotient = $",       quo[12], "_",       quo[8], "_",       quo[4], "_",       quo[0], nl       "Remainder = ", (type uns32 rmndr )    ); end testDiv128; 

You can extend this code to any number of bits by simply adding additional mov/div/mov instructions to the sequence. Like the extended multiplication the previous section presents, this extended precision division algorithm works only for unsigned operands. If you need to divide two signed quantities, you must note their signs, take their absolute values, do the unsigned division, and then set the sign of the result based on the signs of the operands.

If you need to use a divisor larger than 32 bits you're going to have to implement the division using a shift and subtract strategy. Unfortunately, such algorithms are very slow. In this section we'll develop two division algorithms that operate on an arbitrary number of bits. The first is slow but easier to understand; the second is quite a bit faster (in the average case).

As for multiplication, the best way to understand how the computer performs division is to study how you were taught to perform long division by hand. Consider the operation 3456/12 and the steps you would take to manually perform this operation, as shown in Figure 9-3.

Figure 9-3: Manual Digit-by-digit Division Operation.

This algorithm is actually easier in binary because at each step you do not have to guess how many times 12 goes into the remainder nor do you have to multiply 12 by your guess to obtain the amount to subtract. At each step in the binary algorithm the divisor goes into the remainder exactly zero or one times. As an example, consider the division of 27 (11011) by three (11) that is shown in Figure 9-4.

Figure 9-4: Longhand Division in Binary.

There is a novel way to implement this binary division algorithm that computes the quotient and the remainder at the same time. The algorithm is the following:

 Quotient := Dividend; Remainder := 0; for i:= 1 to NumberBits do      Remainder:Quotient := Remainder:Quotient SHL 1;      if Remainder >= Divisor then         Remainder := Remainder - Divisor;         Quotient := Quotient + 1;      endif endfor 

NumberBits is the number of bits in the Remainder, Quotient, Divisor, and Dividend variables. Note that the "Quotient := Quotient + 1;" statement sets the L.O. bit of Quotient to one because this algorithm previously shifts Quotient one bit to the left. The program in Listing 9-3 implements this algorithm.

Listing 9-3: Extended Precision Division.

 program testDiv128b; #include( "stdlib.hhf" ) // div128 // // This procedure does a general 128/128 division operation // using the following algorithm: // (all variables are assumed to be 128-bit objects) // // Quotient := Dividend; // Remainder := 0; // for i:= 1 to NumberBits do // // Remainder:Quotient := Remainder:Quotient SHL 1; // if Remainder >= Divisor then // //     Remainder := Remainder - Divisor; //     Quotient := Quotient + 1; // // endif // endfor // procedure div128 (         Dividend: lword;         Divisor: lword;     var QuotAdrs: lword;     var RmndrAdrs: lword );  @nodisplay; const    Quotient: text := "Dividend"; // Use the Dividend as the Quotient. var    Remainder: lword; begin div128;    push( eax );    push( ecx );    push( edi );    mov( 0, eax ); // Set the remainder to zero.    mov( eax, Remainder[0] );    mov( eax, Remainder[4] );    mov( eax, Remainder[8] );    mov( eax, Remainder[12]);    mov( 128, ecx ); // Count off 128 bits in ECX.    repeat      // Compute Remainder:Quotient := Remainder:Quotient SHL 1:      shl( 1, Dividend[0] ); // See the section on extended      rcl( 1, Dividend[4] ); // precision shifts to see how      rcl( 1, Dividend[8] ); // this code shifts 256 bits to      rcl( 1, Dividend[12]); // the left by one bit.      rcl( 1, Remainder[0] );      rcl( 1, Remainder[4] );      rcl( 1, Remainder[8] );      rcl( 1, Remainder[12]);      // Do a 128-bit comparison to see if the remainder      // is greater than or equal to the divisor.      if      ( #{          mov( Remainder[12], eax );          cmp( eax, Divisor[12] );          ja true;          jb false;          mov( Remainder[8], eax );          cmp( eax, Divisor[8] );          ja true;          jb false;          mov( Remainder[4], eax );          cmp( eax, Divisor[4] );          ja true;          jb false;          mov( Remainder[0], eax );          cmp( eax, Divisor[0] );          jb false;       }# ) then          // Remainder := Remainder - Divisor          mov( Divisor[0], eax );          sub( eax, Remainder[0] );          mov( Divisor[4], eax );          sbb( eax, Remainder[4] );          mov( Divisor[8], eax );          sbb( eax, Remainder[8] );          mov( Divisor[12], eax );          sbb( eax, Remainder[12] );          // Quotient := Quotient + 1;          add( 1, Quotient[0] );          adc( 0, Quotient[4] );          adc( 0, Quotient[8] );          adc( 0, Quotient[12] );       endif;       dec( ecx );    until( @z );    // Okay, copy the quotient (left in the Dividend variable)    // and the remainder to their return locations.    mov( QuotAdrs, edi );    mov( Quotient[0], eax );    mov( eax, [edi] );          mov( Quotient[4], eax );          mov( eax, [edi+4] );          mov( Quotient[8], eax );          mov( eax, [edi+8] );          mov( Quotient[12], eax );          mov( eax, [edi+12] );          mov( RmndrAdrs, edi );          mov( Remainder[0], eax );          mov( eax, [edi] );          mov( Remainder[4], eax );          mov( eax, [edi+4] );          mov( Remainder[8], eax );          mov( eax, [edi+8] );          mov( Remainder[12], eax );          mov( eax, [edi+12] );          pop( edi );          pop( ecx );          pop( eax );       end div128;       // Some simple code to test out the division operation:       static            op1: lword := $8888_8888_6666_6666_4444_4444_2222_2221;            op2: lword := 2;            quo: lword;            rmndr: lword;       begin testDiv128b;          div128( op1, op2, quo, rmndr );          stdout.put          (             nl             nl             "After the division: " nl             nl             "Quotient = $",             quo[12], "_",             quo[8], "_",             quo[4], "_",             quo[0], nl             "Remainder = ", (type uns32 rmndr )       ); end testDiv128b; 

This code looks simple, but there are a few problems with it: It does not check for division by zero (it will produce the value $FFFF_FFFF_FFFF_FFFF if you attempt to divide by zero), it only handles unsigned values, and it is very slow. Handling division by zero is very simple; just check the divisor against zero prior to running this code and return an appropriate error code if the divisor is zero (or raise the ex.DivisionError exception). Dealing with signed values is the same as the earlier division algorithm, note the signs, take the operands' absolute values, do the unsigned division, and then fix the sign afterward. The performance of this algorithm, however, leaves a lot to be desired. It's around an order of magnitude or two worse than the div/idiv instructions on the 80x86, and they are among the slowest instructions on the CPU.

There is a technique you can use to boost the performance of this division by a fair amount: Check to see if the divisor variable uses only 32 bits. Often, even though the divisor is a 128-bit variable, the value itself fits just fine into 32 bits (i.e., the H.O. double words of Divisor are zero). In this special case, which occurs frequently, you can use the div instruction which is much faster. The algorithm is a bit more complex because you have to first compare the H.O. double words for zero, but on the average it runs much faster while remaining capable of dividing any two pair of values.

9.2.7 Extended Precision NEG Operations

Although there are several ways to negate an extended precision value, the shortest way for smaller values (96 bits or less) is to use a combination of neg and sbb instructions. This technique uses the fact that neg subtracts its operand from zero. In particular, it sets the flags the same way the sub instruction would if you subtracted the destination value from zero. This code takes the following form (assuming you want to negate the 64-bit value in EDX:EAX):

 neg( edx ); neg( eax ); sbb( 0, edx ); 

The sbb instruction decrements EDX if there is a borrow out of the L.O. word of the negation operation (which always occurs unless EAX is zero).

To extend this operation to additional bytes, words, or double words is easy; all you have to do is start with the H.O. memory location of the object you want to negate and work toward the L.O. byte. The following code computes a 128-bit negation:

 static      Value: dword[4];       .       .       .      neg( Value[12] );    // Negate the H.O. double word.      neg( Value[8] );     // Neg previous dword in memory.      sbb( 0, Value[12] ); // Adjust H.O. dword.      neg( Value[4] );     // Negate the second dword in the object.      sbb( 0, Value[8] );  // Adjust third dword in object.      sbb( 0, Value[12] ); // Adjust the H.O. dword.      neg( Value );        // Negate the L.O. dword.      sbb( 0, Value[4] );  // Adjust second dword in object.      sbb( 0, Value[8] );  // Adjust third dword in object.      sbb( 0, Value[12] ); // Adjust the H.O. dword. 

Unfortunately, this code tends to get really large and slow because you need to propagate the carry through all the H.O. words after each negate operation. A simpler way to negate larger values is to simply subtract that value from zero:

 static      Value: dword[5]; // 160-bit value.       .       .       .      mov( 0, eax );      sub( Value, eax );      mov( eax, Value );      mov( 0, eax );      sbb( Value[4], eax );      mov( eax, Value[4] );      mov( 0, eax );      sbb( Value[8], eax );      mov( eax, Value[8] );      mov( 0, eax );      sbb( Value[12], eax );      mov( eax, Value[12] );      mov( 0, eax );      sbb( Value[16], eax );      mov( eax, Value[16] ); 

9.2.8 Extended Precision AND Operations

Performing an n-byte AND operation is very easy : Simply AND the corresponding bytes between the two operands, saving the result. For example, to perform the AND operation where all operands are 64 bits long, you could use the following code:

      mov( (type dword source1), eax );      and( (type dword source2), eax );      mov( eax, (type dword dest) );      mov( (type dword source1[4]), eax );      and( (type dword source2[4]), eax );      mov( eax, (type dword dest[4]) ); 

This technique easily extends to any number of words; all you need to is logically AND the corresponding bytes, words, or double words together in the operands. Note that this sequence sets the flags according to the value of the last AND operation. If you AND the H.O. double words last, this sets all but the zero flag correctly. If you need to test the zero flag after this sequence, you will need to logically OR the two resulting double words together (or otherwise compare them both against zero).

9.2.9 Extended Precision OR Operations

Multibyte logical OR operations are performed in the same way as multibyte AND operations. You simply OR the corresponding bytes in the two operands together. For example, to logically OR two 96-bit values, use the following code:

      mov( (type dword source1), eax );      or( (type dword source2), eax );      mov( eax, (type dword dest) );      mov( (type dword source1[4]), eax );      or( (type dword source2[4]), eax );      mov( eax, (type dword dest[4]) );      mov( (type dword source1[8]), eax );      or( (type dword source2[8]), eax );      mov( eax, (type dword dest[8]) ); 

As for the previous example, this does not set the zero flag properly for the entire operation. If you need to test the zero flag after a multiprecision OR, you must logically OR the resulting double words together.

9.2.10 Extended Precision XOR Operations

Extended precision XOR operations are performed in a manner identical to AND/OR: Simply XOR the corresponding bytes in the two operands to obtain the extended precision result. The following code sequence operates on two 64-bit operands, computes their exclusive-or, and stores the result into a 64-bit variable:

      mov( (type dword source1), eax );      xor( (type dword source2), eax );      mov( eax, (type dword dest) );      mov( (type dword source1[4]), eax );      xor( (type dword source2[4]), eax );      mov( eax, (type dword dest[4]) ); 

The comment about the zero flag in the previous two sections applies here.

9.2.11 Extended Precision NOT Operations

The not instruction inverts all the bits in the specified operand. An extended precision NOT is performed by simply executing the not instruction on all the affected operands. For example, to perform a 64-bit NOT operation on the value in (edx:eax), all you need to do is execute the instructions:

      not( eax );      not( edx ); 

Keep in mind that if you execute the not instruction twice, you wind up with the original value. Also note that exclusive-ORing a value with all ones ($FF, $FFFF, or $FFFF_FFFF) performs the same operation as the not instruction.

9.2.12 Extended Precision Shift Operations

Extended precision shift operations require a shift and a rotate instruction. Consider what must happen to implement a 64-bit shl using 32-bit operations (see Figure 9-5):

1. A zero must be shifted into bit zero.

2. Bits zero through 30 are shifted into the next higher bit.

3. Bit 31 is shifted into bit 32.

4. Bits 32 through 62 must be shifted into the next higher bit.

5. Bit 63 is shifted into the carry flag.

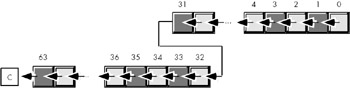
Figure 9-5: 64-Bit Shift Left Operation.

The two instructions you can use to implement this 32-bit shift are shl and rcl. For example, to shift the 64-bit quantity in (EDX:EAX) one position to the left, you'd use the instructions:

      shl( 1, eax );      rcl( 1, eax ); 

Note that using this technique you can only shift an extended precision value one bit at a time. You cannot shift an extended precision operand several bits using the CL register. Nor can you specify a constant value greater than one using this technique.

To understand how this instruction sequence works, consider the operation of these instructions on an individual basis. The shl instruction shifts a zero into bit zero of the 64-bit operand and shifts bit 31 into the carry flag. The rcl instruction then shifts the carry flag into bit 32 and then shifts bit 63 into the carry flag. The result is exactly what we want.

To perform a shift left on an operand larger than 64 bits, you simply use additional rcl instructions. An extended precision shift left operation always starts with the least significant double word, and each succeeding rcl instruction operates on the next most significant double word. For example, to perform a 96- bit shift left operation on a memory location you could use the following instructions:

      shl( 1, (type dword Operand[0]) );      rcl( 1, (type dword Operand[4]) );      rcl( 1, (type dword Operand[8]) ); 

If you need to shift your data by two or more bits, you can either repeat the preceding sequence the desired number of times (for a constant number of shifts) or place the instructions in a loop to repeat them some number of times. For example, the following code shifts the 96-bit value Operand to the left the number of bits specified in ECX:

 ShiftLoop:      shl( 1, (type dword Operand[0]) );      rcl( 1, (type dword Operand[4]) );      rcl( 1, (type dword Operand[8]) );      dec( ecx );      jnz ShiftLoop; 

You implement shr and sar in a similar way, except you must start at the H.O. word of the operand and work your way down to the L.O. word:

 // Double precision SAR:      sar( 1, (type dword Operand[8]) );      rcr( 1, (type dword Operand[4]) );      rcr( 1, (type dword Operand[0]) ); // Double precision SHR:      shr( 1, (type dword Operand[8]) );      rcr( 1, (type dword Operand[4]) );      rcr( 1, (type dword Operand[0]) ); 

There is one major difference between the extended precision shifts described here and their 8-/16-/32-bit counterparts: The extended precision shifts set the flags differently than the single precision operations. This is because the rotate instructions affect the flags differently than the shift instructions. Fortunately, the carry flag is the one you'll test most often after a shift operation and the extended precision shift operations (i.e., rotate instructions) properly set this flag.

The shld and shrd instructions let you efficiently implement multiprecision shifts of several bits. These instructions have the following syntax:

      shld( constant, Operand1, Operand2 );      shld( cl, Operand1, Operand2 );      shrd( constant, Operand1, Operand2 );      shrd( cl, Operand1, Operand2 ); 

The shld instruction works as shown in Figure 9-6.

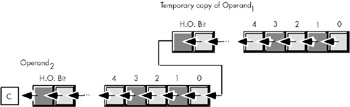
Figure 9-6: SHLD Operation.

Operand₁ must be a 16- or 32-bit register. Operand₂ can be a register or a memory location. Both operands must be the same size. The immediate operand can be a value in the range zero through n-1, where n is the number of bits in the two operands; this operand specifies the number of bits to shift.

The shld instruction shifts bits in Operand₂ to the left. The H.O. bits shift into the carry flag and the H.O. bits of Operand₁ shift into the L.O. bits of Operand₂. Note that this instruction does not modify the value of Operand₁; it uses a temporary copy of Operand₁ during the shift. The immediate operand specifies the number of bits to shift. If the count is n, then shld shifts bit n-1 into the carry flag. It also shifts the H.O. n bits of Operand₁ into the L.O. n bits of Operand₂. The shld instruction sets the flag bits as follows:

• If the shift count is zero, the shld instruction doesn't affect any flags.

• The carry flag contains the last bit shifted out of the H.O. bit of the Operand₂.

• If the shift count is one, the overflow flag will contain one if the sign bit of Operand₂ changes during the shift. If the count is not one, the overflow flag is undefined.

• The zero flag will be one if the shift produces a zero result.

• The sign flag will contain the H.O. bit of the result.

The shrd instruction is similar to shld except, of course; it shifts its bits right rather than left. To get a clear picture of the shrd instruction, consider Figure 9-7.

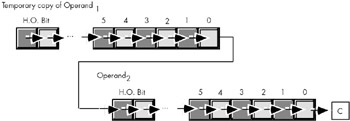
Figure 9-7: SHRD Operation.

The shrd instruction sets the flag bits as follows:

• If the shift count is zero, the shrd instruction doesn't affect any flags.

• The carry flag contains the last bit shifted out of the L.O. bit of the Operand₂.

• If the shift count is one, the overflow flag will contain one if the H.O. bit of Operand₂ changes. If the count is not one, the overflow flag is undefined.

• The zero flag will be one if the shift produces a zero result.

• The sign flag will contain the H.O. bit of the result.

Consider the following code sequence:

 static      ShiftMe: dword[3] := [ $1234, $5678, $9012 ];       .       .       .      mov( ShiftMe[4], eax )      shld( 6, eax, ShiftMe[8] );      mov( ShiftMe[0], eax );      shld( 6, eax, ShiftMe[4] );      shl( 6, ShiftMe[0] ); 

The first shld instruction above shifts the bits from ShiftMe[4] into ShiftMe[8] without affecting the value in ShiftMe[4]. The second shld instruction shifts the bits from ShiftMe into ShiftMe[4]. Finally, the shl instruction shifts the L.O. double word the appropriate amount. There are two important things to note about this code. First, unlike the other extended precision shift left operations, this sequence works from the H.O. double word down to the L.O. double word. Second, the carry flag does not contain the carry out of the H.O. shift operation. If you need to preserve the carry flag at that point, you will need to push the flags after the first shld instruction and pop the flags after the shl instruction.

You can do an extended precision shift right operation using the shrd instruction. It works almost the same way as the preceding code sequence except you work from the L.O. double word to the H.O. double word. The solution is left as an exercise for the reader.

9.2.13 Extended Precision Rotate Operations

The rcl and rcr operations extend in a manner almost identical to shl and shr . For example, to perform 96-bit rcl and rcr operations, use the following instructions:

      rcl( 1, (type dword Operand[0]) );      rcl( 1, (type dword Operand[4]) );      rcl( 1, (type dword Operand[8]) );      rcr( 1, (type dword Operand[8]) );      rcr( 1, (type dword Operand[4]) );      rcr( 1, (type dword Operand[0]) ); 

The only difference between this code and the code for the extended precision shift operations is that the first instruction is a rcl or rcr rather than a shl or shr instruction.

Performing an extended precision rol or ror instruction isn't quite as simple an operation. You can use the bt, shld, and shrd instructions to implement an extended precision rol or ror instruction. The following code shows how to use the shld instruction to do an extended precision rol:

 // Compute ROL( 4, EDX:EAX );          mov( edx, ebx );          shld, 4, eax, edx );          shld( 4, ebx, eax );          bt( 0, eax );        // Set carry flag, if desired. 

An extended precision ror instruction is similar; just keep in mind that you work on the L.O. end of the object first and the H.O. end last.

9.2.14 Extended Precision I/O

Once you have the ability to compute using extended precision arithmetic, the next problem is how do you get those extended precision values into your program and how do you display those extended precision values to the user? HLA's Standard Library provides routines for unsigned decimal, signed decimal, and hexadecimal I/O for values that are 8, 16, 32, 64, or 128 bits in length. So as long as you're working with values whose size is less than or equal to 128 bits in length, you can use the Standard Library code. If you need to input or output values that are greater than 128 bits in length, you will need to write your own procedures to handle the operation. This section discusses the strategies you will need to write such routines.

The examples in this section work specifically with 128-bit values. The algorithms are perfectly general and extend to any number of bits (indeed, the 128-bit algorithms in this section are really nothing more than the algorithms the HLA Standard Library uses for 128-bit values). Of course, if you need a set of 128-bit unsigned I/O routines, you can use the Standard Library code as-is. If you need to handle larger values, simple modifications to the following code are all that should be necessary.

The sections that follow use a common set of 128-bit data types in order to avoid having to coerce lword/uns128/int128 values in each instruction. Here are these types:

 type      h128 :dword[4];      u128 :dword[4];      i128 :dword[4]; 

9.2.14.1 Extended Precision Hexadecimal Output

Extended precision hexadecimal output is very easy. All you have to do is output each double word component of the extended precision value from the H.O. double word to the L.O. double word using a call to the stdout.putd routine. The following procedure does exactly this to output an lword value:

 procedure putb128( b128: h128 ); @nodisplay; begin putb128;      stdout.putd( b128[12] );      stdout.putd( b128[8] );      stdout.putd( b128[4] );      stdout.putd( b128[0] ); end putb128; 

Of course, the HLA Standard Library supplies a stdout.putl procedure that directly writes lword values, so you can call stdout.putl multiple times when outputting larger values (e.g., a 256-bit value). As it turns out, the implementation of the HLA stdlib.putl routine is very similar to putb128, above.

9.2.14.2 Extended Precision Unsigned Decimal Output

Decimal output is a little more complicated than hexadecimal output because the H.O. bits of a binary number affect the L.O. digits of the decimal representation (this was not true for hexadecimal values, which is why hexadecimal output is so easy). Therefore, we will have to create the decimal representation for a binary number by extracting one decimal digit at a time from the number.

The most common solution for unsigned decimal output is to successively divide the value by ten until the result becomes zero. The remainder after the first division is a value in the range 0..9, and this value corresponds to the L.O. digit of the decimal number. Successive divisions by ten (and their corresponding remainder) extract successive digits from the number.

Iterative solutions to this problem generally allocate storage for a string of characters large enough to hold the entire number. Then the code extracts the decimal digits in a loop and places them in the string one by one. At the end of the conversion process, the routine prints the characters in the string in reverse order (remember, the divide algorithm extracts the L.O. digits first and the H.O. digits last, the opposite of the way you need to print them).

In this section, we will employ a recursive solution because it is a little more elegant. The recursive solution begins by dividing the value by ten and saving the remainder in a local variable. If the quotient was not zero, the routine recursively calls itself to print any leading digits first. On return from the recursive call (which prints all the leading digits), the recursive algorithm prints the digit associated with the remainder to complete the operation. Here's how the operation works when printing the decimal value "123":

1. Divide 123 by 10. Quotient is 12; remainder is 3.

2. Save the remainder (3) in a local variable and recursively call the routine with the quotient.

3. [Recursive entry 1.] Divide 12 by 10. Quotient is 1; remainder is 2.

4. Save the remainder (2) in a local variable and recursively call the routine with the quotient.

5. [Recursive entry 2.] Divide 1 by 10. Quotient is 0, remainder is 1.

6. Save the remainder (1) in a local variable. Because the quotient is zero, you don't call the routine recursively.

7. Output the remainder value saved in the local variable (1). Return to the caller (recursive entry 1).

8. [Return to recursive entry 1.] Output the remainder value saved in the local variable in recursive entry 1 (2). Return to the caller (original invocation of the procedure).

9. [Original invocation.] Output the remainder value saved in the local variable in the original call (3). Return to the original caller of the output routine.

The only operation that requires extended precision calculation through this entire algorithm is the "divide by 10" statement. Everything else is simple and straight-forward. We are in luck with this algorithm; because we are dividing an extended precision value by a value that easily fits into a double word, we can use the fast (and easy) extended precision division algorithm that uses the div instruction. The program in Listing 9-4 implements a 128-bit decimal output routine utilizing this technique.

Listing 9-4: 128-Bit Extended Precision Decimal Output Routine.

 program out128; #include( "stdlib.hhf" ); // 128-bit unsigned integer data type: type      u128: dword[4]; // DivideBy10 // // Divides "divisor" by 10 using fast // extended precision division algorithm // that employs the DIV instruction. // // Returns quotient in "quotient" // Returns remainder in eax. // Trashes EBX, EDX, and EDI. procedure DivideBy10( dividend:u128; var quotient:u128 ); @nodisplay; begin DivideBy10;    mov( quotient, edi );    xor( edx, edx );    mov( dividend[12], eax );    mov( 10, ebx );    div( ebx, edx:eax );    mov( eax, [edi+12] );    mov( dividend[8], eax );    div( ebx, edx:eax );    mov( eax, [edi+8] );    mov( dividend[4], eax );    div( ebx, edx:eax );    mov( eax, [edi+4] );    mov( dividend[0], eax );    div( ebx, edx:eax );    mov( eax, [edi+0] );    mov( edx, eax ); end DivideBy10; // Recursive version of putu128. // A separate "shell" procedure calls this so that // this code does not have to preserve all the registers // it uses (and DivideBy10 uses) on each recursive call. procedure recursivePutu128( b128:u128 ); @nodisplay; var    remainder: byte; begin recursivePutu128;      // Divide by ten and get the remainder (the char to print).      DivideBy10( b128, b128 );      mov( al, remainder ); // Save away the remainder (0..9).      // If the quotient (left in b128) is not zero, recursively      // call this routine to print the H.O. digits.      mov( b128[0], eax ); // If we logically OR all the dwords      or( b128[4], eax );  // together, the result is zero if and      or( b128[8], eax );  // only if the entire number is zero.      or( b128[12], eax );      if( @nz ) then          recursivePutu128( b128 );      endif;      // Okay, now print the current digit.      mov( remainder, al );      or( '0', al );       // Converts 0..9 -> '0..'9'.      stdout.putc( al ); end recursivePutu128; // Non-recursive shell to the above routine so we don't bother // saving all the registers on each recursive call. procedure putu128( b128:uns128 ); @nodisplay; begin putu128;    push( eax );    push( ebx );    push( edx );    push( edi );    recursivePutu128( b128 );    pop( edi );    pop( edx );    pop( ebx );    pop( eax ); end putu128; // Code to test the routines above: static    b0: u128 := [0, 0, 0, 0];          // decimal = 0    b1: u128 := [1234567890, 0, 0, 0]; // decimal = 1234567890    b2: u128 := [$8000_0000, 0, 0, 0]; // decimal = 2147483648    b3: u128 := [0, 1, 0, 0 ];         // decimal = 4294967296    // Largest uns128 value    // (decimal=340,282,366,920,938,463,463,374,607,431,768,211,455):    b4: u128 := [$FFFF_FFFF, $FFFF_FFFF, $FFFF_FFFF, $FFFF_FFFF ]; begin out128;    stdout.put( "b0 = " );    putu128( b0 );    stdout.newln();    stdout.put( "b1 = " );    putu128( b1 );    stdout.newln();    stdout.put( "b2 = " );    putu128( b2 );    stdout.newln();    stdout.put( "b3 = " );    putu128( b3 );    stdout.newln(); stdout.put( "b4 = " ); putu128( b4 ); stdout.newln(); end out128; 

9.2.14.3 Extended Precision Signed Decimal Output

Once you have an extended precision unsigned decimal output routine, writing an extended precision signed decimal output routine is very easy. The basic algorithm takes the following form:

• Check the sign of the number. If it is positive, call the unsigned output routine to print it.

• If the number is negative, print a minus sign. Then negate the number and call the unsigned output routine to print it.

To check the sign of an extended precision integer, of course, you simply test the H.O. bit of the number. To negate a large value, the best solution is to probably subtract that value from zero. Here's a quick version of puti128 that uses the putu128 routine from the previous section.

 procedure puti128( i128: int128 ); nodisplay; begin puti128;      if( (type int32 i128[12]) < 0 ) then           stdout.put( '-' );           // Extended Precision Negation:           push( eax );           mov( 0, eax );           sub( i128[0], eax );           mov( eax, i128[0] );           mov( 0, eax );           sbb( i128[4], eax );           mov( eax, i128[4] );           mov( 0, eax );           sbb( i128[8], eax );           mov( eax, i128[8] );           mov( 0, eax );           sbb( i128[12], eax );           mov( eax, i128[12] );           pop( eax );    endif;    putu128( (type uns128 i128)); end puti128; 

9.2.14.4 Extended Precision Formatted Output

The code in the previous two sections prints signed and unsigned integers using the minimum number of necessary print positions. To create nicely formatted tables of values you will need the equivalent of a puti128Size or putu128Size routine. Once you have the "unformatted" versions of these routines, implementing the formatted versions is very easy.

The first step is to write an i128Size and a u128Size routine that compute the minimum number of digits needed to display the value. The algorithm to accomplish this is very similar to the numeric output routines. In fact, the only difference is that you initialize a counter to zero upon entry into the routine (e.g., the non-recursive shell routine), and you increment this counter rather than outputting a digit on each recursive call. (Don't forget to increment the counter inside i128Size if the number is negative; you must allow for the output of the minus sign.) After the calculation is complete, these routines should return the size of the operand in the EAX register.

Once you have the i128Size and u128Size routines, writing the formatted output routines is very easy. Upon initial entry into puti128Size or putu128Size, these routines call the corresponding "size" routine to determine the number of print positions for the number to display. If the value that the "size" routine returns is greater than the absolute value of the minimum size parameter (passed into puti128Size or putu128Size), all you need to do is call the put routine to print the value, no other formatting is necessary. If the absolute value of the parameter size is greater than the value i128Size or u128Size returns, then the program must compute the difference between these two values and print that many spaces (or other filler character) before printing the number (if the parameter size value is positive) or after printing the number (if the parameter size value is negative). The actual implementation of these two routines is left as an exercise (or just check out the source code in the HLA Standard Library for the stdout.putiSize128 and stdout.putuSize128 routines).

The HLA Standard Library implements the i128Size and u128Size by doing a set of successive extended precision comparisons to determine the number of digits in the values. Interested readers may want to take a look at the source code for these routines as well as the source code for the stdout.puti128 and stdout.putu128 procedures (this source code appears on the accompanying CD-ROM).

9.2.14.5 Extended Precision Input Routines

There are a couple of fundamental differences between the extended precision output routines and the extended precision input routines. First of all, numeric output generally occurs without possibility of error;^[3] numeric input, on the other hand, must handle the very real possibility of an input error such as illegal characters and numeric overflow. Also, HLA's Standard Library and run-time system encourage a slightly different approach to input conversion. This section discusses those issues that differentiate input conversion from output conversion.

Perhaps the biggest difference between input and output conversion is the fact that output conversion is not bracketed. That is, when converting a numeric value to a string of characters for output, the output routine does not concern itself with characters preceding the output string, nor does it concern itself with the characters following the numeric value in the output stream. Numeric output routines convert their data to a string and print that string without considering the context (i.e., the characters before and after the string representation of the numeric value). Numeric input routines cannot be so cavalier; the contextual information surrounding the numeric string is very important.

A typical numeric input operation consists of reading a string of characters from the user and then translating this string of characters into an internal numeric representation. For example, a statement like "stdin.get(i32);" typically reads a line of text from the user and converts a sequence of digits appearing at the beginning of that line of text into a 32-bit signed integer (assuming i32 is an int32 object). Note, however, that the stdin.get routine skips over certain characters in the string that may appear before the actual numeric characters. For example, stdin.get automatically skips any leading spaces in the string. Likewise, the input string may contain additional data beyond the end of the numeric input (for example, it is possible to read two integer values from the same input line), therefore the input conversion routine must somehow determine where the numeric data ends in the input stream. Fortunately, HLA provides a simple mechanism that lets you easily determine the start and end of the input data: the Delimiters character set.

The Delimiters character set is a variable, internal to the HLA Standard Library, which contains the set of legal characters that may precede or follow a legal numeric value. By default, this character set includes the end of string marker (a zero byte), a tab character, a line feed character, a carriage return character, a space, a comma, a colon, and a semicolon. Therefore, HLA's numeric input routines will automatically ignore any characters in this set that occur on input before a numeric string. Likewise, characters from this set may legally follow a numeric string on input (conversely, if any non-delimiter character follows the numeric string, HLA will raise an ex.ConversionError exception).

The Delimiters character set is a private variable inside the HLA Standard Library. Although you do not have direct access to this object, the HLA Standard Library does provide two accessor functions, conv.setDelimiters and conv.getDelimiters that let you access and modify the value of this character set. These two functions have the following prototypes (found in the conv.hhf header file):

 procedure conv.setDelimiters( Delims:cset ); procedure conv.getDelimiters( var Delims:cset ); 

The conv.setDelimiters procedure will copy the value of the Delims parameter into the internal Delimiters character set. Therefore, you can use this procedure to change the character set if you want to use a different set of delimiters for numeric input. The conv.getDelimiters call returns a copy of the internal Delimiters character set in the variable you pass as a parameter to the conv.getDelimiters procedure. We will use the value returned by conv.getDelimiters to determine the end of numeric input when writing our own extended precision numeric input routines.

When reading a numeric value from the user, the first step will be to get a copy of the Delimiters character set. The second step is to read and discard input characters from the user as long as those characters are members of the Delimiters character set. Once a character is found that is not in the Delimiters set, the input routine must check this character and verify that it is a legal numeric character. If not, the program should raise an ex.IllegalChar exception if the character's value is outside the range $00..$7f or it should raise the ex.ConversionError exception if the character is not a legal numeric character. Once the routine encounters a numeric character, it should continue reading characters as long as they valid numeric characters; while reading the characters the conversion routine should be translating them to the internal representation of the numeric data. If, during conversion, an overflow occurs, the procedure should raise the ex.ValueOutOfRange exception.

Conversion to numeric representation should end when the procedure encounters the first delimiter character at the end of the string of digits. However, it is very important that the procedure does not consume the delimiter character that ends the string. So the following is incorrect:

 static      Delimiters: cset;            .            .            .      conv.getDelimiters( Delimiters );      // Skip over leading delimiters in the string:      while( stdin.getc() in Delimiters ) do /* getc did the work */ endwhile;      while( al in '0'..'9') do          // Convert character in AL to numeric representation and          // accumulate result...          stdin.getc();       endwhile;       if( al not in Delimiters ) then          raise( ex.ConversionError ); endif; 

The first while loop reads a sequence of delimiter characters. When this first while loop ends, the character in AL is not a delimiter character. So far, so good. The second while loop processes a sequence of decimal digits. First, it checks the character read in the previous while loop to see if it is a decimal digit; if so, it processes that digit and reads the next character. This process continues until the call to stdin.getc (at the bottom of the loop) reads a non-digit character. After the second while loop, the program checks the last character read to ensure that it is a legal delimiter character for a numeric input value.

The problem with this algorithm is that it consumes the delimiter character after the numeric string. For example, the colon symbol is a legal delimiter in the default Delimiters character set. If the user types the input "123:456" and executes the code above, this code will properly convert "123" to the numeric value one hundred twenty-three. However, the very next character read from the input stream will be the character "4" not the colon character (":"). While this may be acceptable in certain circumstances, most programmers expect numeric input routines to consume only leading delimiter characters and the numeric digit characters. They do not expect the input routine to consume any trailing delimiter characters (e.g., many programs will read the next character and expect a colon as input if presented with the string "123:456"). Because stdin.getc consumes an input character, and there is no way to "put the character back" onto the input stream, some other way of reading input characters from the user, that doesn't consume those characters, is needed.^[4]

The HLA Standard Library comes to the rescue by providing the stdin.peekc function. Like stdin.getc, the stdin.peekc routine reads the next input character from HLA's internal buffer. There are two major differences between stdin.peekc and stdin.getc. First, stdin.peekc will not force the input of a new line of text from the user if the current input line is empty (or you've already read all the text from the input line). Instead, stdin.peekc simply returns zero in the AL register to indicate that there are no more characters on the input line. Because #0 is (by default) a legal delimiter character for numeric values, and the end of line is certainly a legal way to terminate numeric input, this works out rather well. The second difference between stdin.getc and stdin.peekc is that stdin.peekc does not consume the character read from the input buffer. If you call stdin.peekc several times in a row, it will always return the same character; likewise, if you call stdin.getc immediately after stdin.peekc, the call to stdin.getc will generally return the same character as returned by stdin.peekc (the only exception being the end-of-line condition). So although we cannot put characters back onto the input stream after we've read them with stdin.getc, we can peek ahead at the next character on the input stream and base our logic on that character's value. A corrected version of the previous algorithm might be the following:

 static      Delimiters: cset;            .            .            .      conv.getDelimiters( Delimiters );      // Skip over leading delimiters in the string:      while( stdin.peekc() in Delimiters ) do          // If at the end of the input buffer, we must explicitly read a          // new line of text from the user. stdin.peekc does not do this          // for us.          if( al = #0 ) then              stdin.ReadLn();          else                stdin.getc(); // Remove delimiter from the input stream.          endif;    endwhile;    while( stdin.peekc in '0'..'9') do          stdin.getc();       // Remove the input character from the input stream.          // Convert character in AL to numeric representation and          // accumulate result...    endwhile;    if( al not in Delimiters ) then          raise( ex.ConversionError );    endif; 

Note that the call to stdin.peekc in the second while does not consume the delimiter character when the expression evaluates false. Hence, the delimiter character will be the next character read after this algorithm finishes.

The only remaining comment to make about numeric input is to point out that the HLA Standard Library input routines allow arbitrary underscores to appear within a numeric string. The input routines ignore these underscore characters. This allows the user to input strings like "FFFF_F012" and "1_023_596" which are a little more readable than "FFFFF012" or "1023596". To allow underscores (or any other symbol you choose) within a numeric input routine is quite simple; just modify the second while loop above as follows:

 while( stdin.peekc in {'0'..'9', '_'}) do    stdin.getc(); // Read the character from the input stream.    // Ignore underscores while processing numeric input.    if( al <> '_' ) then          // Convert character in AL to numeric representation and          // accumulate result...    endif; endwhile; 

9.2.14.6 Extended Precision Hexadecimal Input

As was the case for numeric output, hexadecimal input is the easiest numeric input routine to write. The basic algorithm for hexadecimal string to numeric conversion is the following:

• Initialize the extended precision value to zero.

• For each input character that is a valid hexadecimal digit, do the following:

• Convert the hexadecimal character to a value in the range 0..15 ($0..$F).

• If the H.O. four bits of the extended precision value are non-zero, raise an exception.

• Multiply the current extended precision value by 16 (i.e., shift left four bits).

• Add the converted hexadecimal digit value to the accumulator.

• Check the last input character to ensure it is a valid delimiter. Raise an exception if it is not.

The program in Listing 9-5 implements this extended precision hexadecimal input routine for 128-bit values.

Listing 9-5: Extended Precision Hexadecimal Input.

 program Xin128; #include( "stdlib.hhf" ); // 128-bit unsigned integer data type: type    b128: dword[4]; procedure getb128( var inValue:b128 ); @nodisplay; const    HexChars := {'0'..'9', 'a'..'f', 'A'..'F', '_'}; var    Delimiters: cset;    LocalValue: b128; begin getb128;    push( eax );    push( ebx );    // Get a copy of the HLA standard numeric input delimiters:    conv.getDelimiters( Delimiters );    // Initialize the numeric input value to zero:    xor( eax, eax );    mov( eax, LocalValue[0] );    mov( eax, LocalValue[4] );    mov( eax, LocalValue[8] );    mov( eax, LocalValue[12] );    // By default, #0 is a member of the HLA Delimiters    // character set. However, someone may have called    // conv.setDelimiters and removed this character    // from the internal Delimiters character set. This    // algorithm depends upon #0 being in the Delimiters    // character set, so let's add that character in    // at this point just to be sure.    cs.unionChar( #0, Delimiters );    // If we're at the end of the current input    // line (or the program has yet to read any input),    // for the input of an actual character.    if( stdin.peekc() = #0 ) then    stdin.readLn(); endif; // Skip the delimiters found on input. This code is // somewhat convoluted because stdin.peekc does not // force the input of a new line of text if the current // input buffer is empty. We have to force that input // ourselves in the event the input buffer is empty. while( stdin.peekc() in Delimiters ) do    // If we're at the end of the line, read a new line    // of text from the user; otherwise, remove the    // delimiter character from the input stream.    if( al = #0 ) then       stdin.readLn(); // Force a new input line.    else       stdin.getc(); // Remove the delimiter from the input buffer.    endif; endwhile; // Read the hexadecimal input characters and convert // them to the internal representation: while( stdin.peekc() in HexChars ) do    // Actually read the character to remove it from the    // input buffer.    stdin.getc();    // Ignore underscores, process everything else.    if( al <> '_' ) then       if( al in '0'..'9' ) then          and( $f, al ); // '0'..'9' -> 0..9 else          and( $f, al ); // 'a'/'A'..'f'/'F' -> 1..6          add( 9, al ); // 1..6 -> 10..15    endif;    // Conversion algorithm is the following:    //    // (1) LocalValue := LocalValue * 16.    // (2) LocalValue := LocalValue + al    //    // Note that "* 16" is easily accomplished by    // shifting LocalValue to the left four bits.    //    // Overflow occurs if the H.O. four bits of LocalValue    // contain a non-zero value prior to this operation.    // First, check for overflow:    test( $F0, (type byte LocalValue[15]));    if( @nz ) then       raise( ex.ValueOutOfRange );    endif;    // Now multiply LocalValue by 16 and add in    // the current hexadecimal digit (in EAX).    mov( LocalValue[8], ebx );    shld( 4, ebx, LocalValue[12] );    mov( LocalValue[4], ebx );    shld( 4, ebx, LocalValue[8] );    mov( LocalValue[0], ebx );    shld( 4, ebx, LocalValue[4] );    shl( 4, ebx );    add( eax, ebx );    mov( ebx, LocalValue[0] );   endif; endwhile; // Okay, we've encountered a non-hexadecimal character. // Let's make sure it's a valid delimiter character. // Raise the ex.ConversionError exception if it's invalid. if( al not in Delimiters ) then       raise( ex.ConversionError );    endif;    // Okay, this conversion has been a success. Let's store    // away the converted value into the output parameter.    mov( inValue, ebx );    mov( LocalValue[0], eax );    mov( eax, [ebx] );    mov( LocalValue[4], eax );    mov( eax, [ebx+4] );    mov( LocalValue[8], eax );    mov( eax, [ebx+8] );    mov( LocalValue[12], eax );    mov( eax, [ebx+12] );    pop( ebx );    pop( eax ); end getb128; // Code to test the routines above: static      b1:b128; begin Xin128;    stdout.put( "Input a 128-bit hexadecimal value: " );    getb128( b1 );    stdout.put    (       "The value is: $",       b1[12], '_',       b1[8], '_',       b1[4], '_',       b1[0],       nl    ); end Xin128; 

Extending this code to handle objects that are not 128 bits long is very easy. There are only three changes necessary: You must zero out the whole object at the beginning of the getb128 routine; when checking for overflow (the "test( $F, (type byte LocalValue[15]));" instruction) you must test the H.O. 4 bits of the new object you're processing; and you must modify the code that multiplies LocalValue by 16 (via shld) so that it multiplies your object by 16 (i.e., shifts it to the left four bits).

9.2.14.7 Extended Precision Unsigned Decimal Input

The algorithm for extended precision unsigned decimal input is nearly identical to that for hexadecimal input. In fact, the only difference (beyond only accepting decimal digits) is that you multiply the extended precision value by 10 rather than 16 for each input character (in general, the algorithm is the same for any base; just multiply the accumulating value by the input base). The code in Listing 9-6 demonstrates how to write a 128-bit unsigned decimal input routine.

Listing 9-6: Extended Precision Unsigned Decimal Input.

 program Uin128; #include( "stdlib.hhf" ); // 128-bit unsigned integer data type: type    u128: dword[4]; procedure getu128( var inValue:u128 ); @nodisplay; var     Delimiters: cset;     LocalValue: u128;     PartialSum: u128; begin getu128;     push( eax );     push( ebx );     push( ecx );     push( edx );     // Get a copy of the HLA standard numeric input delimiters:     conv.getDelimiters( Delimiters );     // Initialize the numeric input value to zero:     xor( eax, eax );     mov( eax, LocalValue[0] );     mov( eax, LocalValue[4] );     mov( eax, LocalValue[8] );     mov( eax, LocalValue[12] );     // By default, #0 is a member of the HLA Delimiters     // character set. However, someone may have called     // conv.setDelimiters and removed this character     // from the internal Delimiters character set. This     // algorithm depends upon #0 being in the Delimiters     // character set, so let's add that character in     // at this point just to be sure.     cs.unionChar( #0, Delimiters );     // If we're at the end of the current input     // line (or the program has yet to read any input),     // for the input of an actual character.     if( stdin.peekc() = #0 ) then         stdin.readLn();     endif;     // Skip the delimiters found on input. This code is     // somewhat convoluted because stdin.peekc does not     // force the input of a new line of text if the current     // input buffer is empty. We have to force that input     // ourselves in the event the input buffer is empty.     while( stdin.peekc() in Delimiters ) do          // If we're at the end of the line, read a new line          // of text from the user; otherwise, remove the          // delimiter character from the input stream.          if( al = #0 ) then              stdin.readLn(); // Force a new input line.          else             stdin.getc(); // Remove the delimiter from the input buffer.          endif;    endwhile;    // Read the decimal input characters and convert    // them to the internal representation:    while( stdin.peekc() in '0'..'9' ) do       // Actually read the character to remove it from the       // input buffer.       stdin.getc();       // Ignore underscores, process everything else.       if( al <> '_' ) then          and( $f, al ); // '0'..'9' -> 0..9          mov( eax, PartialSum[0] ); // Save to add in later.          // Conversion algorithm is the following:          //          // (1) LocalValue := LocalValue * 10.          // (2) LocalValue := LocalValue + al          //          // First, multiply LocalValue by 10:          mov( 10, eax );          mul( LocalValue[0], eax );          mov( eax, LocalValue[0] );          mov( edx, PartialSum[4] );          mov( 10, eax );          mul( LocalValue[4], eax );          mov( eax, LocalValue[4] );          mov( edx, PartialSum[8] );          mov( 10, eax );          mul( LocalValue[8], eax );          mov( eax, LocalValue[8] );          mov( edx, PartialSum[12] );          mov( 10, eax );          mul( LocalValue[12], eax );          mov( eax, LocalValue[12] );          // Check for overflow. This occurs if EDX          // contains a non-zero value.          if( edx /* <> 0 */ ) then             raise( ex.ValueOutOfRange );          endif;          // Add in the partial sums (including the          // most recently converted character).          mov( PartialSum[0], eax );          add( eax, LocalValue[0] );          mov( PartialSum[4], eax );          adc( eax, LocalValue[4] );          mov( PartialSum[8], eax );          adc( eax, LocalValue[8] );          mov( PartialSum[12], eax );          adc( eax, LocalValue[12] );          // Another check for overflow. If there          // was a carry out of the extended precision          // addition above, we've got overflow.          if( @c ) then             raise( ex.ValueOutOfRange );          endif;       endif;    endwhile;    // Okay, we've encountered a non-decimal character.    // Let's make sure it's a valid delimiter character.    // Raise the ex.ConversionError exception if it's invalid.    if( al not in Delimiters ) then       raise( ex.ConversionError );    endif;    // Okay, this conversion has been a success. Let's store    // away the converted value into the output parameter.    mov( inValue, ebx );    mov( LocalValue[0], eax );    mov( eax, [ebx] );    mov( LocalValue[4], eax );    mov( eax, [ebx+4] );    mov( LocalValue[8], eax );    mov( eax, [ebx+8] );    mov( LocalValue[12], eax );    mov( eax, [ebx+12] );    pop( edx );    pop( ecx );    pop( ebx );    pop( eax ); end getu128; // Code to test the routines above: static    b1:u128; begin Uin128;    stdout.put( "Input a 128-bit decimal value: " );    getu128( b1 );    stdout.put    (       "The value is: $",       b1[12], '_',       b1[8], '_',       b1[4], '_',       b1[0],       nl    ); end Uin128; 

As for hexadecimal input, extending this decimal input to some number of bits beyond 128 is fairly easy. All you need do is modify the code that zeros out the LocalValue variable and the code that multiplies LocalValue by ten (overflow checking is done in this same code, so there are only two spots in this code that require modification).

9.2.14.8 Extended Precision Signed Decimal Input

Once you have an unsigned decimal input routine, writing a signed decimal input routine is easy. The following algorithm describes how to accomplish this:

• Consume any delimiter characters at the beginning of the input stream.

• If the next input character is a minus sign, consume this character and set a flag noting that the number is negative.

• Call the unsigned decimal input routine to convert the rest of the string to an integer.

• Check the return result to make sure its H.O. bit is clear. Raise the ex.ValueOutOfRange exception if the H.O. bit of the result is set.

• If the code encountered a minus sign in step two above, negate the result.

The actual code is left as a programming exercise (or see the conversion routines in the HLA Standard Library for concrete examples).

^[1]Newer C standards also provide for a "long long int", which is usually a 64-bit integer.

^[2]Windows may translate this to an ex.IntoInstr exception.

^[3]Technically speaking, this isn't entirely true. It is possible for a device error (e.g., disk full) to occur. The likelihood of this is so low that we can effectively ignore this possibility.

^[4]The HLA Standard Library routines actually buffer up input lines in a string and process characters out of the string. This makes it easy to "peek" ahead one character when looking for a delimiter to end the input value. Your code can also do this; however, the code in this chapter will use a different approach.