Chapter 5: Trees and Graphs

Trees and graphs are common data structures in programming, so they are both fair game in a programming interview. Trees, in particular, appear frequently because they enable an interviewer to test your knowledge of recursion and run-time analysis. Trees are also simple enough that you can implement them within the time constraints of an interview. Although graph problems are interesting, they are usually very complicated and do not lend themselves to interview problems. Therefore, the emphasis of this chapter is on trees.

Unlike Chapter 4’s use of C/C++ in the problems, in this and the subsequent chapters you’re going to use more modern languages like C# and Java. This means you’ll be creating classes to properly encapsulate your code and you generally won’t be using pointers anymore.

Trees

A tree is made up of nodes (data elements) with zero, one, or several references to other nodes. Each node has only one other node referencing it. The result is a data structure that looks like Figure 5-1.

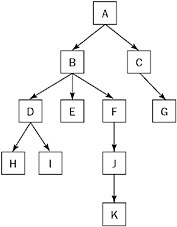
Figure 5-1

As in a linked list, a node is represented by a structure or class, and trees can be implemented in any language that includes pointers or references. In object-oriented languages you usually define a class for the common parts of a node, and one or more subclasses for the data held by a node. For example, these are the C# classes you might use for a tree of integers:

 public class Node {     public Node[] children; } public class IntNode : Node {     public int value; }

In this definition, children is an array that keeps track of all the nodes that this node references. Note that for simplicity we exposed the children as public data members. A proper class definition would make them private and expose methods to manipulate them. A fuller Java equivalent (with methods and constructors) to the preceding classes would be as follows:

 public abstract class Node {     private Node[] children;     public Node( Node[] children ){         this.children = children;     }     public int getNumChildren(){         return children.length;     }     public Node getChild( int index ){         return children[ index ];     } } public class IntNode extends Node {     private int value;     public IntNode( Node[] children, int value ){         super( children );         this.value = value;     }     public int getValue(){         return value;     } }

Even this example is not complete, however, because there is no error handling and no way to dynamically add or remove nodes from a tree. During an interview you may want to keep things simple by using public data members, folding classes together, or by only sketching out the various methods that are needed to manage the tree. For the latter, you could also define an interface instead of a base class and not bother defining the methods. Ask the interviewer how much detail is wanted and design your code accordingly. If the interviewer provides no guidance, be sure to explain your choices as you go along.

Looking at the tree shown in Figure 5-1, you can see that there is only one top-level node. From this node, it is possible to follow pointers and reach every other node. This top-level node is called the root. The root is the only node from which you are guaranteed to have a path to every other node. The root node is inherently the start of any tree. Therefore, people will often say “tree” when talking about the root node of the tree.

Following is some additional tree-related vocabulary:

• Parent - A node that points to other nodes is the parent of those nodes. Every node except the root has one parent. In Figure 5-1, B is the parent of D, E, and F.

• Child - A node is the child of any node that points to it. In Figure 5-1, each of the nodes D, E, and F is a child of B.

• Descendant - All the nodes that can be reached by following a path of child nodes from a particular node are the descendants of that node. In Figure 5-1, D, E, F, H, I, J, and K are the descendants of B.

• Ancestor - An ancestor of a node is any other node for which the node is a descendant. For example, A, B, and D are the ancestors of I.

• Leaves - The leaves are nodes that do not have any children. G, H, I, and K are leaves.

Binary Trees

So far, you’ve been using the most general definition of a tree. In practice, when an interviewer says “tree,” he or she usually means a special type of tree called a binary tree. In a binary tree, each node has no more than two children, commonly referred to as right and left. Figure 5-2 shows an example of a binary tree.

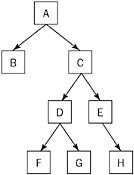
Figure 5-2

Here’s a simple implementation of a binary tree. For simplicity, we combine everything into a single class:

 public class Node {     private Node left;     private Node right;     private int  value;     public Node( Node left, Node right, int value ){         this.left = left;         this.right = right;         this.value = value;     }     public Node getLeft() { return left; }     public Node getRight() { return right; }     public int getValue() { return value; } }

When an element has no left or right child, the corresponding reference is null.

Problems involving only binary trees can often be solved more quickly than equivalent problems about generic trees, but they are no less challenging. Because time is at a premium in an interview, most tree problems will be binary tree problems. If an interviewer just says “tree,” it’s a good idea to clarify whether he or she is referring to a generic tree or a binary tree.

Tip 

People often say “tree” when they mean “binary tree.”

Binary Search Trees

Trees are often used to store sorted or ordered data. By far, the most common way to store data in a tree is using a special tree called a binary search tree (BST). In a BST, the value held by a node’s left child is less than or equal to its own value, and the value held by a node’s right child is greater than or equal to its value. In effect, the data in a BST is sorted by value: All the descendants to the left of a node are less than or equal to the node and all the descendants to the right of the node are greater than or equal to the node. Figure 5-3 is an example of a BST.

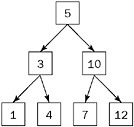
Figure 5-3

BSTs are so common, in fact, that many people mean a BST when they say “tree.” Again, ask for clarification before proceeding.

Tip 

People often say “tree” when they mean “binary search tree.”

Lookup

One advantage of a binary search tree is that the lookup operation (locating a particular node in the tree) is fast and simple. This is particularly useful for data storage. In outline form, the algorithm to perform a lookup in a BST is as follows:

 Start at the root node Loop while current node is non-null     If the current node's value is equal to your value         Return the current node     If the current node's value is less than your value         Make the right node your current node     If the current node's value is greater than your value         Make the left node your current node End loop

If you fall out of the loop, the node wasn’t in the tree.

Here’s one way to code the search in C# or Java:

 Node findNode( Node root, int value ){     while( root != null ){         int currval = root.getValue();         if( currval == value ) break;         if( currval < value ){             root = root.getRight();         } else { // currval > value             root = root.getLeft();         }     }     return root; }

This lookup is a fast operation because you eliminate half the nodes from your search on each iteration by choosing to follow the left subtree or the right subtree. In the worst case, you will know whether the lookup was successful by the time there is only one node left to search. Therefore, the running time of the lookup is equal to the number of times that you can halve n nodes before you get to 1. This number, x, is the same as the number of times you can double 1 before reaching n, and it can be expressed as 2^x = n. You can find x using a logarithm. For example, log₂ 8 = 3 because 2³ = 8, and so the running time of the lookup operation is O(log₂(n)). It is common to omit the base 2 and call this O(log(n)). log(n) is very fast. Consider that log₂1,000,000,000 ( 30. Logarithms with different bases differ by a constant factor, so the base is ignored in big-O notation.

Tip 

Lookup is an O(log(n)) operation in a binary search tree.

Note one caveat to saying that lookup is O(log(n)) in a BST. Lookup is only O(log(n)) if you can guarantee that the number of nodes remaining to be searched will be halved or nearly halved on each iteration. In the worst case, each node has only one child. In such a case, you have a linked list because each node points to only one other node. Lookup then becomes an O(n) operation just as in a linked list. The good news is that there are ways to guarantee that every node has approximately the same number of nodes on its left side as its right. A tree with approximately the same number of nodes on each side is called a balanced tree.

Tip 

Of the methods to guarantee that every node has approximately the same number of nodes per side, the most common is called a red-black tree.

Without going into too much detail (as the special cases get very nasty), it is also possible to delete and insert into a balanced BST in O(log(n)) time.

Tip 

Deletion and insertion are O(log(n)) operations in binary search trees.

Binary search trees have other important properties. For example, it is possible to obtain the smallest element by following all the left children, and to obtain the largest element by following all the right children. The nodes can also be printed out, in order, in O(n) time. It is even possible, given a node, to find the next-highest node in O(log(n)) time.

Tree problems are often designed to test your ability to think recursively. Each node in a tree is the root of a subtree beginning at that node. This subtree property is conducive to recursion because recursion generally involves solving a problem in terms of similar subproblems and a base case. In tree recursion you start with a root, perform an action, and then move to the left or right subtree (or both, one after the other). This process continues until you reach a null reference, which is the end of a tree (and a good base case). For example, the preceding lookup operation can be reimplemented recursively as follows:

 Node findNode( Node root, int value ){     if( root == null ) return null;     int currval = root.getValue();     if( currval == value ) return root;     if( currval < value ){         return findNode( root.getRight(), value );     } else { // currval > value         return findNode( root.getLeft(), value );     } }

Most problems with trees have this recursive form. A good way to start thinking about any problem involving a tree is to start thinking recursively.

Tip 

Many tree operations can be implemented recursively.

Heaps

Another common tree is a heap. Heaps are trees (usually binary trees) with a twist: Each child of a node has a value less than or equal to the node’s own value. (The data implementation of a heap, however, can be different from what we discussed previously.) Consequently, the root node always has the largest value in the tree, which means that it’s possible to find the maximum value in constant time: Simply return the root value. Insertion and deletion are still O(log(n)), but lookup becomes O(n). It is not possible to find the next-higher node to a given node in O(log(n)) time or to print out the nodes in sorted order in O(n) time as in a BST.

You could model the patients waiting in a hospital emergency room with a heap. As each patient enters, he or she is assigned a priority and put into the heap. A heart attack patient would get a higher priority than a patient with a stubbed toe. When a doctor becomes available, the doctor would want to examine the patient with the highest priority. The doctor can determine the patient with the highest priority by extracting the max value from the heap, which is a constant time operation.

Tip 

If extracting the max value needs to be fast, then use a heap.

Common Searches

It’s nice when you have a tree with ordering properties such as a BST or a heap. Often you’re given a tree that isn’t a BST or a heap. For example, you may have a tree that is a representation of a family tree or a company job hierarchy. You have to use different techniques to retrieve data from this kind of tree. One common class of problems involves searching for a particular node. Two very common search algorithms are used to accomplish this task.

Breadth-First Search

One way to search a tree is to do a breadth-first search (BFS). In a BFS you start with the root, move left to right across the second level, then move left to right across the third level, and so forth. You continue the search until either you have examined all of the nodes or you find the node you are searching for. The time to find a node is O(n), so this type of search is best avoided for large trees. A BFS also uses a large amount of memory because it is necessary to track the child nodes for all nodes on a given level while searching that level.

Depth-First Search

Another common way to search for a node is by using a depth-first search (DFS). A depth-first search follows one branch of the tree down as many levels as possible until the target node is found or the end is reached. When the search can’t go down any farther, it is continued at the nearest ancestor with unexplored children. DFS has much lower memory requirements than BFS because it is not necessary to store all of the child pointers at each level. In addition, DFS has the advantage that it doesn’t examine any single level last (BFS examines the lowest level last). This is useful if you suspect that the node you are searching for will be in the lower levels. For example, if you were searching a job hierarchy tree looking for an employee who started less than three months ago, you would suspect that lower-level employees are more likely to have started recently. In this case, if the assumption were true, a DFS would usually find the target node more quickly than a BFS.

There are other types of searches, but these are the two most common that you will encounter in an interview.

Traversals

Another common type of tree problem is called a traversal. As opposed to a search, where you look for a particular node and stop when you find it, a traversal visits every node and performs some operation on it. There are many types of traversals, each of which visits nodes in a different order, but you’re only likely to be asked about the three most common types of traversal for binary trees:

• Preorder traversal of a node performs the operation first on the node itself, then on its left descendants, and finally on its right descendants. In other words, a node is always visited before any of its children.

• Inorder traversal performs the operation first on the node’s left descendants, then on the node itself, and finally on its right descendants. In other words, the left subtree is visited first, then the node itself, and then the node’s right subtree.

• Postorder traversal performs the operation first on the node’s left descendants, then on the node’s right descendants, and finally on the node itself. In other words, all of a node’s children are visited before the node itself.

These traversals can also happen with nonbinary trees as long as you have a way to classify whether a child is “less than” (on the left of) or “greater than” (on the right of) its parent node.

Recursion is usually the simplest way to implement a traversal. See the problems in the chapter for some examples.

Tip 

If you’re asked to implement a traversal, recursion is a good way to start thinking about the problem.