Trigonometry

Trigonometry is the study of triangles . I'm sure you know what a triangle is, so I'm not going to get medieval and start defining things from ground 0. Instead, I want to start by looking at a special kind of triangle that we all know and love: the right triangle.

A Right Triangle

A right triangle is defined as any triangle that has one right angle. A right angle is defined as an angle of exactly 90 degrees. When drawn on paper, a right triangle is denoted by a small square in the corner that is a right angle (90 degrees). Figure 8.1 shows a few right triangles with their right angles marked .

Figure 8.1: A few right triangles with their right angles marked.

Triangles are divided into sides and angles, and every triangle has three of each. The side that opposes the right angle is called the hypotenuse of the right triangle. The two remaining sides are sometimes called legs . It is customary to give letters to the sides of a triangle for notational sake. Typically, the legs are labeled a and b and the hypotenuse is labeled c, as shown in Figure 8.2. Further, the angles are typically labeled A, B, and C, and the label of each angle corresponds to the side that it opposes. Therefore, angle C is the right angle because it opposes the hypotenuse (side c). This is true of angle A and side a, as well as angle B and side b. Refer to Figure 8.2.

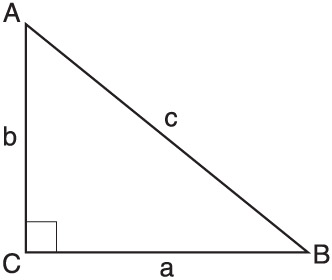
Figure 8.2: A right triangle has its legs labeled a and b and its hypotenuse labeled c. The angles are labeled A, B, and C.

Right triangles have some special properties because one angle is fixed at 90 degrees. In fact, all of trigonometry is based on the relation of the lengths of the sides of a triangle to the measure of the angles formed by those sides.

The Pythagorean Theorem

Pythagoras, a 6th-century philosopher and mathematician , discovered that the length of the hypotenuse of a right triangle, when squared, is equal to the sum of the squares of the legs. That sounds complex, but it really isn't. Consider the following equation, which defines what Pythagoras is talking about:

The idea is that the length of the hypotenuse (c), when squared (c ² ), is equal to the sum of the squares of the sides (a ² + b ² ).

This equation is known as the Pythagorean Theorem . It has many uses, including being able to find the distance between two points, given their coordinates.

The Distance Formula

Consider Figure 8.3, which shows two points on the stage. The stage is a Cartesian plane, much like you learned about in geometry class, with an X and a Y axis.

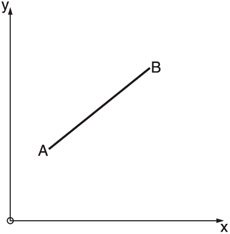
Figure 8.3: We want to find the distance between two points, A and B.

We can now draw a right triangle between the two points, as shown in Figure 8.4.

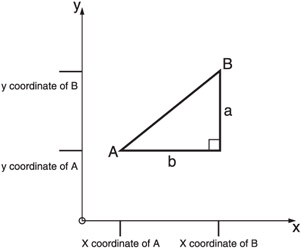
Figure 8.4: We draw a right triangle between the points A and B. The sides opposite points A and B are labeled a and b.

As you can see, we've constructed our triangle so that the hypotenuse is the line from point A to point B. Now we can use the Pythagorean Theorem to determine the length of this hypotenuse, which will be the same as the distance between the points.

If you look at the triangle in Figure 8.4, you can see that the length of the bottom leg (side a) can be found by subtracting the x coordinate of point A from the x coordinate of point B. That gives us the length of the first leg (side b). The second leg (side a) is found by taking the difference of the y coordinates of point B and A. The following equations give us the exact lengths of the legs:

Note  

Please note that when referring to the coordinates of a point, I use a subscript x and subscript y for the respective points. In other words, if I have a point A(4,5), then A _x would be 4 and A _y would be 5.

If we now plug these for a and b in the Pythagorean Theorem, we get the following equation:

Finally, we can take the square root of both sides to solve for the variable c, leaving us with the distance equation:

If I were to tell you that the actual coordinates of point A were (4, 6) and the actual coordinates of point B were (6, 8), you could plug these values into the preceding equation to produce the following:

Now let's solve this equation by doing the work to get a numerical value for c:

And as you can see, the actual distance between the points A(4, 6) and B(6,8) is 2.8284.

Therefore, this new formula can give us the distance between any two points if we know their coordinates. Let's implement this in Flash now, while we're looking at it.

Implementing the Distance Formula in Flash

We already know the distance formula. Implementing the formula in Flash amounts to creating a function that takes two objects (movie clips usually) as arguments and returns the distance between them. Consider the following:

 function dist(obj1,obj2){     return Math.sqrt(Math.pow(obj1._x-obj2._x, 2) + Math.pow(obj1._y-obj2._y, 2)); } 

Now we can instantly find the distance between any two objects that have the _x and _y properties defined.

Relative Distance and the Improved Distance Formula

Now that we have the distance formula figured out, it's time to change it. I've mentioned before how important it is to make your script efficient so that your games play smoothly. Well, here in our implementation of the distance formula, we have an opportunity to improve things.

As an example, let's say that we have an object on the stage and we want to know when the mouse comes within a certain distance of the object. This kind of setup is called a bounding circle because we use a circular boundary around the object to hit test against.

The circle, shown in Figure 8.5, has its radius labeled. The radius is the distance from the center of the circle to its edge. If the distance from the mouse to the center of the circle becomes less than the radius of the circle, the mouse is inside it.

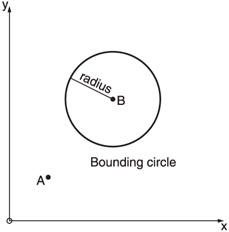
Figure 8.5: The point B is inside a bounding circle.

To solve this problem, we could simply create an onEnterFrame handler that checks the distance from the mouse to the circle's center. If this distance becomes less than the radius of the circle, we know there is a hit. Let's take a look at what that might look like in code.

First assume a new Flash movie with a circle in the library. The circle's registration point is at the center of the circle:

 attachMovie("circle"," circle",1); circle.radius = circle._width/2; circle.onEnterFrame = function(){     obj=new Object();     obj._x = _xmouse;     obj._y = _ymouse;     if(dist(obj, circle) < circle.radius)         trace("hit!!"); } //add distance equation here 

This example works because for each frame, the distance formula is called and the distance from the mouse to the circle is compared with the circle radius. That's great, but where is the room for improvement?

The improvement comes from the distance formula. The last thing the function does before returning its value is to take the square root. That's an expensive operation in terms of CPU, and doing one every frame is hardly efficient. After you've added many clips to the stage, each taking one square root every frame, you have a lot of work going on to calculate them. If you had no other choice, you would have to take the square root and live with it. But the fact is, you do have a choice.

What would happen if, when we set the radius for the circle, we squared the actual radius? That would mean that the radius that Flash would be working with would be the square of the actual radius. Now when we perform the comparison with the distance from the mouse to the center of the circle, we can leave off that final square root. In other words, we would compare the square of the distance to the square of the radius. The result is identical to what we did earlier: a bounding circle hit test.

We need to add a call to Math.pow to square the radius when we set it. Notice that is done only once the entire time the program runs. In exchange, we can omit the Math.sqrt call in the distance formula, which was called once every frame. Nice tradeoff , eh?

To make things clear and reusable, I define a new function called dist2 , which is equivalent to the distance squared. Then I redefine the old dist function to take advantage of the new dist2 function:

 function dist2(obj1,obj2){     //distance formula without the square root     return Math.pow(obj1._x-obj2._x, 2) + Math.pow(obj1._y-obj2._y, 2) } function dist(obj1,obj2){     //square root of distance squared gives distance  return Math.sqrt(dist2(obj1,obj2));  } 

Sometimes you need the exact distance, but for the most part, this new dist2 function works perfectly . Consider the following upgrade to the previous example:

 attachMovie("circle"," circle",1); circle.radius =  Math.pow(circle._width/2, 2);  circle.onEnterFrame = function(){     obj=new Object();     obj._x = _xmouse;     obj._y = _ymouse;     if(  dist2(obj, circle)  < circle.radius)         trace("hit!!"); } 

The Problem of Movement Revisited

Now that we have the distance formula under our belts, we can look again at the subject of moving things around on the stage in any direction we want with a fixed speed (distance moved per frame or per second).

Using some algebra, the distance formula, and your thinking cap, you might already be able to see how this is possible. Let me explain. Let's say that we want our circle to move 5 pixels closer to the mouse every frame. Let the circle be point B and the mouse be point A from Figure 8.5.

If the distance is 20 pixels apart, we know that the ratio of the required distance to the actual distance is 5 to 20. (We want to move at a rate of 5, the distance is currently 20, so our ratio is 5:20, or 1:4.) Now think of this movement as the hypotenuse of a right triangle. The other two sides are the horizontal and vertical components of the movement.

If we scaled the hypotenuse of a right triangle down from 20 pixels to 5 pixels by dividing by 4, the other two sides of the triangle have to be scaled by the same amount to keep the triangle looking like a smaller version of the old triangle. Therefore, all we would have to do is divide the other two sides by 4 to get the length of their sides. Because these sides correspond to the X and Y distance, we now have the X and Y constituent values for moving 5 pixels in the specified direction. Look at Figure 8.6 to see what I mean.

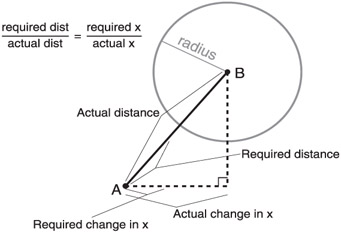
Figure 8.6: The ratio of the required distance and the actual distance is the same as the ratio between the required change in x and the actual change in x.

Because the two ratios are the same (equal), we can create an equation for them, as follows :

And conveniently, we know three of those fields already. The only thing we don't know is the required change in x. Because the other three values are known, we can plug them in and solve for the unknown. Let's rewrite the equation using everything we know:

In this equation, speed is the distance we want to travel each step (frame). This is divided by the distance from A to B. That ratio is set equal to the ratio between delta x (our unknown change in x) and the difference in x values between the two objects. Let's write the equation solved for delta x to be explicit:

We can construct the same equation for y:

Therefore, to find the required change in x and y, we would plug in the values we know and solve for delta x and delta y. Those changes would then be applied to the coordinates of point B (the one we want to move).

That's a good bit of algebra, so I want to solidify with some script examples now. Let's go back and fix the Mouse Chaser game so that the bat chases the mouse in a direct line. In that game, we had a function called moveBat that handled the bat's movement. If we remove that function and replace it with a new function, based on the algebra we've been doing, the new bat should move correctly and everything will be groovy. First let's look at the old moveBat function:

 function moveBat(){     caughtMouse = false;     //move bat horizontally     if(bat._x < _root._xmouse - speed)bat._x += speed;     else if(bat._x > _root._xmouse + speed)bat._x -= speed;     else caughtMouse = true;     //move back vertically     if(bat._y < _root._ymouse - speed)bat._y += speed;     else if(bat._y > _root._ymouse + speed)bat._y -= speed;     else if(caughtMouse == true)resetGame(); } 

Now let's use our triangle to make sure we know what's going on. Look at Figure 8.7.

Figure 8.7: We create a right triangle between the bat and the mouse so that we can compute the bat's new coordinates.

Now it's time to implement, based on our preceding equations and our new triangle drawing:

 function moveBat(){     var p = new Object();     p._x = _xmouse; p._y = _ymouse;     var d = dist(p,bat);     if(d < speed){         resetGame();         return;     }     bat._x += ((_xmouse - bat._x)*speed)/d;     bat._y += ((_ymouse - bat._y)*speed)/d; } 

The new function begins by setting up an object called p that contains _x and _y properties so that it can be used with our dist function, which is then called on p and bat . If this distance is smaller than the speed, the mouse has been caught and we can reset the game and return from the function. If the distance is larger than the speed, we update the bat's position by adding the delta x and delta y values, which are the result of the implementation of our previous equations. I have placed a file called mouse chaser improved.fla in the Chapter 8 directory of the CD. This file contains the new-and-improved moveBat function.