BACKGROUND

Genetic Programming and Artificial Neural Networks

Genetic Programming (GP) (Koza, 1992) is an evolutionary method used to create computer programs that represent approximate or exact solutions to a problem. This technique allows for the finding of programs with the shape of a tree, and, in its most common application, those programs will be mathematical expressions combining mathematical operators, input variables , constants, decision rules, relational operators, etc.

All of these possible operators must be specified before starting the search. So, with them, GP must be able to build trees with the objective of finding the desired expression which models the relation between the input variables and the desired output. This set of operators is divided into two groups: the terminal set contains the operators which cannot accept parameters, like variables or constants; and the function set , which contains the operators, such as add or subtract, which need parameters. Once the terminal and non-terminal operators are specified, it is possible to establish types. Each node will have a type, and the construction of child expressions needs to follow the rules of the nodal type (Montana, 1995).

GP creates automatic program generation by means of a process based on the evolution theory of (Darwin, 1864), in which, after subsequent generations, new trees (individuals) are produced from old ones by means of crossover, copy and mutation (see Fuchs, 1998; Luke & Spector, 1998), based on natural selection; the best trees will have more chances of being chosen to become part of the next generation. Thus, a stochastic process is established which, after successive generations, obtains a well- adapted tree.

As the programs we are obtaining with GP have the shape of trees, GP can be adapted to many different kinds of problems. The problem proposed in this chapter is extracting knowledge from databases. We will show how we can solve it with GP in two different ways in a classification problem: by extracting a rule (with the shape of an IF-THEN-ELSE rule) that makes classifications, and by extracting different rules, one for each classification class.

In the field of knowledge discovery from databases, one of the most successful applications of GP is in the development of fuzzy rules (see Fayyad et al., 1996; Bonarini, 1996), mixing its ability to develop rules and using the technique of Automatically Defined Functions (ADF), described in Koza (1994), for obtaining fuzzy rules. In a recent work done by Wong and Leung (2000), GP is applied as a knowledge extraction technique from databases, and they present LOGENPRO (Logic Grammar Based Genetic Algorithm). They combine GP and representation of knowledge in first order logic. This first approximation shows the advantages of GP as a KDD (Knowledge Discovery in Databases) extraction technique.

GP was also used as a rule extraction technique in combination with decision trees, where the functions in the nodes of the trees use one or more variables (Bot, 1999), but this combination makes the algorithm design very complicated. More recently, Engelbrecht et al. (2001) applied GP and decision trees to extract knowledge from databases, designing an algorithm called BGP (Building-Block Approach to Genetic Programming). In this algorithm, GP is combined with decision trees, but, in this case, it is centered in the concept of a building block, which represents a condition or a node of the tree. A building block has three parts: an attribute, a relational operator, and a threshold. Rules are obtained by combining different values of the parts of the building blocks in the shape of decision trees.

A new research area is the use of GP to extract knowledge from Artificial Neural Networks (ANNs). An ANN (see Lippmann, 1987; Haykin, 1999) is an information-processing system based on generalizations of human cognition or neural biology. An ANN consists of many simple computational neural units connected to each other. An input is presented to its input units, this input vector is propagated through the whole network, and finally, some kind of output is spit out. The most common type of ANN (and the one used in this chapter) consists of different layers with some neurons on each and connected with feed-forward connections (i.e., the exit of one neuron cannot go to the entrance of a neuron of the same or previous layer) and trained with the backpropagation algorithm (Johansson et al., 1992).

ANNs have proven to be a powerful tool in many different applications, but they have a big problem. The reasoning process they follow cannot be explained, i.e. there is no clear relationship between the inputs presented to the network and the outputs they return. To solve this problem, GP can be applied to perform rule extraction on these pairs of given inputs/returned outputs in order to be able to understand the behavior of ANNs.

Description of the Problem

The iris flower data (SAS Institute, 1988) were originally published by Fisher (1936) as examples of discriminant analysis and cluster analysis. Four parameters, sepal length, sepal width, petal length and petal width , were measured in millimeters on 50 iris specimens from each of three species, Iris setosa, Iris versicolor and Iris virginica . Given the four parameters, one should be able to determine which of the three classes a specimen belongs to. There are 150 data points listed in the database.

One of the reasons for applying this problem is the physical situation of the classes in the four-dimensional space. Figure 1 shows the space distribution for variables X ₁ and X ₂ (petal length and petal width). As shown in Duch et al. (2000), with these two variables, we can get a higher discrimination for the three classes, a fitness of a 98 percent success using only these two variables. So, they are an important reference point for comparing the results graphically.

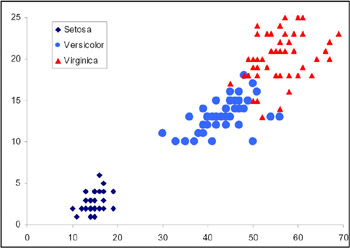
Figure 1: Distribution of the Three Classes

In this chapter, we will show how we can use GP and ANNs to solve the iris flower problem. When we use GP, we will see two different points of view. In the first, we will use GP to obtain a rule classifier system ( one-tree classification); in the second, we will try to find a Boolean expression for each of the three species to determine if the data belongs to that class (three-tree classification).

We will also use an ANN to solve this problem and, in order to understand the network obtained, we will use GP to extract the rules that explain its behavior. We will see how GP seems to be a suitable technique, not just for classifying problems, but also for extracting knowledge from databases and ANNs and data mining in general.