TEXT CLASSIFICATION

Let D be a collection of m documents d _i , i = 1 m , each one belonging to one or more of c categories (topics) c _j , j = 1 c . The document feature vector space D ⁿ is defined through the term “document matrix, TF , where tf _ki is the frequency of occurrence of the k ^th term, k = 1 n , to the i ^th document of the collection.

A text classifier is a mapping f from the document feature vector space D ⁿ to the category vector space C ^c . The category vector space is defined through the category-document matrix CD , where cd _ji ˆˆ { 0,1 } is the information of whether the i ^th document belongs to the j ^th category. To create such a mapping using machine learning, we need to split the document collection into a training set and a test set, and then use these sets to create and test the classifiers respectively.

Table 1: Term-Document Matrix TF

	d 1		d i		d m
t 1	tf 11		tf 1i		tf 1m
t k	tf k1		tf ki		tf km
t n	tf ni		tf ni		tf nm

Table 2: Category-Document Matrix CD

	Training Set				Test Set
	d 1			d i	d i + 1			d m
c 1	cd 11			cd 1i	cd 1 ( i + 1 )			cd 1m
c j	cd j1			cd ji	cd j ( i + 1 )			cd jm
c c	cd c1			cd ci	cd c ( i + 1 )			cd cm

Support Vector Machines (SVMs)

In this work, we used Support Vector Machines (SVMs) as text classifiers (Dumais, 1998). The SVM model was proposed by Vapnik in 1979. In recent years , it has gained much popularity due to its strong theoretical and empirical justification. In the simplest linear form, a SVM is a hyperplane that separates a set of positive examples from a set of negative examples with maximum margin. A separating hyperplane (Cherkassky, 1998) is a linear function capable of separating the training data in the classification problem without error. Suppose that the training data consist of n samples ( x ₁ , y ₁ ), , ( x _n , y _n ), x _i ˆˆ R ^d , y _i ˆˆ {+ 1 , ˆ’ 1 }, which can be separated by a hyperplane decision function

with appropriate coefficients w and w . A separating hyperplane satisfies the constraints that define the separation of data samples:

The minimal distance from the separating hyperplane to the closest data point is called the margin , denoted by T . A separating hyperplane is called "optimal" if the margin is the maximum size . It is intuitively clear that a larger margin corresponds to better generalization.

The key to finding the optimal hyperplane is to find the coefficient vector w that maximizes the margin T , or equivalently minimizing

with respect to both w and w .

In the case of training data that cannot be separated without error, positive slack variables ¾ _i , i = 1 , , n can be introduced to quantify the nonseparable data in the defining condition of the hyperplane:

For a training sample x _i , the slack variable ¾ _i is the deviation from the margin border corresponding to the class of y _i . Slack variables greater then 0 correspond to nonseparable points, while slack variables greater than 1 correspond to misclassified samples.

It is possible to pose the problem in terms of quadratic optimization by introducing the following equivalent formulation concept of the soft margin hyperplane. This hyperplane is defined by the coefficients w , w that minimize the functional:

subject to the constraints and given sufficiently large (fixed) C . In this form, the coefficient C affects the trade-off between the complexity and proportion of nonseparable samples, and it must be selected by the user .

To relieve the problem of nonlinear separability, a nonlinear mapping of the training data into a high-dimensional feature space is usually performed according to Cover's theorem on the separability of patterns (Haykin, 1999). The separating hyperplane is now defined as a linear function of vectors drawn from the feature space rather than from the original input space. This expansion is usually realized based on a Radial-Basis inner product kernel:

where the width ƒ ² is specified a priory by the user and is common to all the kernels .

The constrained optimization problem is solved using the method of Lagrange multipliers. In this work, we used the OSU SVM Classifier Matlab Toolbox (OSU SVM) to train classifiers.

To obtain a good performance, the parameters C and ƒ (in the case of a Radial-Basis kernel) of the SVM model have to be chosen carefully (Duan, 2001). These "higher level" parameters are usually referred to as hyperparameters.

To provide an accurate measure of confidence, Platt (2000) proposed a parametric approach for SVM. This approach consists of finding the parameters A and B of a sigmoid function, and then mapping the scores f _i = D ( x _i ) =( w · x _i ) + w into probability estimates

such that the negative log- likelihood cross-entropy error function of the data

is minimized using maximum likelihood estimation.

Na ve Bayes

Bayes theorem can be used to estimate the probability Pr(c _j d _i ) that a document d _i is in class c _j .

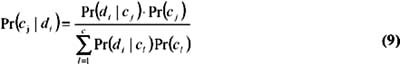
where Pr(c _j ) is the prior probability that a document is in class c _j , and where Pr(d _i c _j ) is the likelihood of observing document d _i in class c _j .

, the estimate of Pr(c _j ), can be calculated from the fraction of the training documents that is assigned to this class:

The probability of observing a document like d _i in class c _j is based on the naive assumption that a word's occurrence in class c _j is independent of the occurrences of the other words. Therefore, Pr(d _i c _j ) is:

where t _k represents the k ^th term of the collection document. The estimation of P(d _i c _j ) is now reduced to the estimation of P(t _k c _j ) (Laplace estimator ), which is the likelihood of observing t _k in class c _j :

where tf( t _k ,c _j ) is the number of occurrences of the word t _k in category c _j , and where n is the number of the terms of the corpus .

In this work, we have used the NB algorithm for multi-topic categorization, so we define a threshold h _j related to each category j . If Pr(c _j d _i )>h _j , then document d _i is categorized under category c _j . Threshold selection is performed by measuring the F1-measure in a validation set (Sebastiani, 2002).