15.6 Coercion Semantics for Subtyping

---

15.6 Coercion Semantics for Subtyping

Throughout this chapter, our intuition has been that subtyping is "semantically insignificant." The presence of subtyping does not change the way programs are evaluated; rather, subtyping is just a way of obtaining additional flexibility in typing terms. This interpretation is simple and natural, but it carries some performance penalties-particularly for numerical calculations and for accessing record fields-that may not be acceptable in high-performance implementations. We sketch here an alternative coercion semantics and discuss some new issues that it, in its turn, raises. This section can be skipped if desired.

Problems with the Subset Semantics

As we saw in §15.5, it can be convenient to allow subtyping between different base types. But some "intuitively reasonable" inclusions between base types may have a detrimental effect on performance. For example, suppose we introduce the axiom Int <: Float, so that integers can be used in floating-point calculations without writing explicit coercions-allowing us to write, for example, 4.5 + 6 instead of 4.5 + intToFloat(6). Under the subset semantics, this implies that the set of integer values must literally be a subset of the set of floats. But, on most real machines, the concrete representations of integers and floats are entirely different: integers are usually represented in twos-complement form, while floats are divided up into mantissa, exponent, and sign, plus some special cases such as NaN (not-a-number).

To reconcile these representational differences with the subset semantics of subtyping, we can adopt a common tagged (or boxed) representation for numbers: an integer is represented as a machine integer plus a tag (either in a separate header word or in the high-order bits of the same word as the actual integer), and a float is represented as a machine float plus a different tag. The type Float then refers to the entire set of tagged numbers (floats and ints), while Int refers just to the tagged ints.

This scheme is not unreasonable: it corresponds to the representation strategy actually used in many modern language implementations, where the tag bits (or words) are also needed to support garbage collection. The downside is that every primitive operation on numbers must actually be implemented as a tag check on the arguments, a few instructions to unbox the primitive numbers, one instruction for the actual operation, and a couple of instructions for re-boxing the result. Clever compiler optimizations can eliminate some of this overhead, but, even with the best currently available techniques, it significantly degrades performance, especially in heavily numeric code such as graphical and scientific calculations.

A different performance problem arises when records are combined with subtyping-in particular, with the permutation rule. Our simple evaluation rule for field projection

can be read as "search for l_j among the labels of the record, and yield the associated value v_j." But, in a real implementation, we certainly do not want to perform a linear search at run time through the fields of the record to find the desired label. In a language without subtyping (or with subtyping but without the permutation rule), we can do much better: if the label l_j appears third in the type of the record, then we know statically that all run-time values with this type will have l_j as their third field, so at run time we do not need to look at the labels at all (in fact, we can omit them completely from the run-time representation, effectively compiling records into tuples). To obtain the value of the l_j field, we generate an indirect load through a register pointing to the start of the record, with a constant offset of 3 words. The presence of the permutation rule foils this technique, since knowing that some record value belongs to a type where l_j appears as the third field tells us nothing at all, now, about where the l_j field is actually stored in the record. Again, clever optimizations and run-time tricks can palliate this problem, but in general field projection can require some form of search at run time.^[4]

Coercion Semantics

We can address both of these problems by adopting a different semantics, in which we "compile away" subtyping by replacing it with run-time coercions. If an Int is promoted to a Float during typechecking, for example, then at run time we physically change this number's representation from a machine integer to a machine float. Similarly, a use of the record permutation subtyping rule will be compiled into a piece of code that literally rearranges the order of the fields. Primitive numeric operations and field accesses can now proceed without the overhead of unboxing or search.

Intuitively, the coercion semantics for a language with subtyping is expressed as a function that transforms terms from this language into a lower-level language without subtyping. Ultimately, the low-level language might be machine code for some concrete processor. For purposes of illustration, however, we can keep the discussion on a more abstract level. For the source language, we choose the one we have been using for most of the chapter-the simply typed lambda-calculus with subtyping and records. For the low-level target language, we choose the pure simply typed lambda-calculus with records and a Unit type (which we use to interpret Top).

Formally, the compilation consists of three translation functions-one for types, one for subtyping, and one for typing. For types, the translation just replaces Top with Unit. We write this function as 〚-〛.

•  

  〚Top〛	=	Unit
  〚T1→T2〛	=	〚T1〛→〚T2〛
  〚{li:TiiÎ1..n}〛	=	{li:〚Ti〛iÎi..n}

For example, 〚Top→{a:Top,b:Top}〛 = Unit→{a:Unit,b:Unit}. (The other translations will also be written 〚-〛; the context will always make it clear which one we are talking about.)

To translate a term, we need to know where subsumption is used in typechecking it, since these are the places where run-time coercions will be inserted. One convenient way of formalizing this observation is to give the translation as a function on derivations of typing statements. Similarly, to generate a coercion function transforming values of type S to type T, we need to know not just that S is a subtype of T, but also why. We accomplish this by generating coercions from subtyping derivations.

A little notation for naming derivations is needed to formalize the translations. Write C :: S <: T to mean "C is a subtyping derivation tree whose conclusion is S <: T." Similarly, write D :: Г ⊢ t : T to mean "D is a typing derivation whose conclusion is Г ⊢ t : T.

Let us look first at the function that, given a derivation C for the subtyping statement S <: T, generates a coercion 〚C〛. This coercion is nothing but a function (in the target language of the translation, λ_→) from type 〚S〛 to type 〚T〛. The definition goes by cases on the final rule used in C.

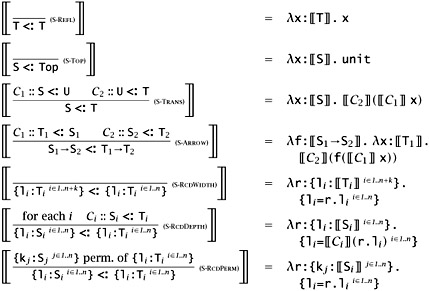
15.6.1 Lemma

If C :: S <: T, then ⊢ 〚C〛 : 〚S〛 →〚T〛.

Proof: Straightforward induction on C.

Typing derivations are translated in a similar way. If D is a derivation of the statement Г ⊢ t: T, then its translation 〚D〛 is a target-language term of type 〚T〛. This translation function is often called the Penn translation, after the group at the University of Pennsylvania that first studied it (Breazu-Tannen, Coquand, Gunter, and Scedrov, 1991).

15.6.2 Theorem

If D :: Г ⊢ t : T, then 〚Г〛 ⊢ 〚D〛 : 〚T〛, where 〚Г〛 is the point-wise extension of the type translation to contexts: 〚ø〛 = ø and 〚Г, x:T〛 = 〚Г〛, x: 〚T〛.

Proof: Straightforward induction on D, using Lemma 15.6.1 for the T-SUB case.

Having defined these translations, we can drop the evaluation rules for the high-level language with subtyping, and instead evaluate terms by typechecking them (using the high-level typing and subtyping rules), translating their typing derivations to the low-level target language, and then using the evaluation relation of this language to obtain their operational behavior. This strategy is actually used in some high-performance implementations of languages with subtyping, such as the Yale compiler group's experimental Java compiler (League, Shao, and Trifonov, 1999; League, Trifonov, and Shao, 2001).

15.6.3 Exercise [⋆⋆⋆ ↛]

Modify the translations above to use simply typed lambda-calculus with tuples (instead of records) as a target language. Check that Theorem 15.6.2 still holds.

Coherence

When we give a coercion semantics for a language with subtyping, there is a potential pitfall that we need to be careful to avoid. Suppose, for example, that we extend the present language with the base types Int, Bool, Float, and String. The following primitive coercions might all be useful:

•  

  〚Bool <: Int〛	=	λb:Bool. if b then 1 else 0
  〚Int <: String〛	=	intToString
  〚Bool <: Float〛	=	λb:Bool. if b then 1.0 else 0.0
  〚Float <: String〛	=	floatToString

The functions intToString and floatToString are primitives that construct string representations of numbers. For the sake of the example, suppose that intToString(1) = "1", while floatToString(1.0) = "1.000".

Now, suppose we are asked to evaluate the term

   (λx:String.x) true; 

using the coercion semantics. This term is typable, given the axioms above for the primitive types. In fact, it is typable in two distinct ways: we can either use subsumption to promote Bool to Int and then to String, to show that true is an appropriate argument to a function of type String→String, or we can promote Bool to Float and then to String. But if we translate these derivations into λ_→, we get different behaviors. If we coerce true to type Int, we get 1, from which intToString yields the string "1". But if we instead coerce true to a float and then, using floatToString, to a String (following the structure of a typing derivation in which true : String is proved by going via Float), we obtain "1.000". But "1" and "1.000" are very different strings: they do not even have the same length. In other words, the choice of how to prove ⊢ (λx:String. x) true : String affects the way the translated program behaves! But this choice is completely internal to the compiler-the programmer writes only terms, not derivations-so we have designed a language in which programmers cannot control or even predict the behavior of the programs they write.

The appropriate response to such problems is to impose an additional requirement, called coherence, on the definition of the translation functions.

15.6.4 Definition

A translation 〚-〛 from typing derivations in one language to terms in another is coherent if, for every pair of derivations D₁ and D₂ with the same conclusion Г ⊢ t : T, the translations 〚D₁〛 and 〚D₂〛 are behaviorally equivalent terms of the target language.

In particular, the translations given above (with no base types) are coherent. To recover coherence when we consider base types (with the axioms above), it suffices to change the definition of the floatToString primitive so that floatToString(0.0) = "0" and floatToString(1.0) = "1".

Proving coherence, especially for more complex languages, can be a tricky business. See Reynolds (1980), Breazu-Tannen et al. (1991), Curien and Ghelli (1992), and Reynolds (1991).

^[4]Similar observations apply to accessing fields and methods of objects, in languages where object subtyping allows permutation. This is the reason that Java, for example, restricts subtyping between classes so that new fields can only be added at the end. Subtyping between interfaces (and between classes and interfaces) does allow permutation-if it did not, interfaces would be of hardly any use-and the manual explicitly warns that looking up a method from an interface will in general be slower than from a class.

---