12.1 Normalization for Simple Types

---

12.1 Normalization for Simple Types

The calculus we shall consider here is the simply typed lambda-calculus over a single base type A. Normalization for this calculus is not entirely trivial to prove, since each reduction of a term can duplicate redexes in subterms. ^[1]

12.1.1 Exercise [⋆]

Where do we fail if we attempt to prove normalization by a straightforward induction on the size of a well-typed term?

The key issue here (as in many proofs by induction) is finding a strong enough induction hypothesis. To this end, we begin by defining, for each type T, a set R_T of closed terms of type T. We regard these sets as predicates and write R_T(t) for t Î R_T.^[2]

12.1.2 Definition

• R_A(t) iff t halts.

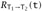• iff t halts and, whenever 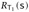, we have .

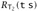This definition gives us the strengthened induction hypothesis that we need. Our primary goal is to show that all programs-i.e., all closed terms of base type-halt. But closed terms of base type can contain subterms of functional type, so we need to know something about these as well. Moreover, it is not enough to know that these subterms halt, because the application of a normalized function to a normalized argument involves a substitution, which may enable more evaluation steps. So we need a stronger condition for terms of functional type: not only should they halt themselves, but, when applied to halting arguments, they should yield halting results.

The form of Definition 12.1.2 is characteristic of the logical relations proof technique. (Since we are just dealing with unary relations here, we should more properly say logical predicates.) If we want to prove some property P of all closed terms of type A, we proceed by proving, by induction on types, that all terms of type A possess property P, all terms of type A→A preserve property P, all terms of type (A→A)→(A→A) preserve the property of preserving property P, and so on. We do this by defining a family of predicates, indexed by types. For the base type A, the predicate is just P. For functional types, it says that the function should map values satisfying the predicate at the input type to values satisfying the predicate at the output type.

We use this definition to carry out the proof of normalization in two steps. First, we observe that every element of every set R_T is normalizable. Then we show that every well-typed term of type T is an element of R_T.

The first step is immediate from the definition of R_T:

12.1.3 Lemma

If R_T(t), then t halts.

The second step is broken into two lemmas. First, we remark that membership in R_T is invariant under evaluation.

12.1.4 Lemma

If t : T and t → t′, then R_T(t) iff R_T(t′).

Proof: By induction on the structure of the type T. Note, first, that it is clear that t halts iff t′ does. If T = A, there is nothing more to show. Suppose, on the other hand, that T = T₁ → T₂ for some T₁ and T₂. For the "only if" direction (  ) suppose that R_T(t) and that for some arbitrary s : T₁. By definition we have But t s → t′ s, from which the induction hypothesis for type T₂ gives us . Since this holds for an arbitrary s, the definition of R_T gives us R_T(t′). The argument for the "if" direction (  ) is analogous.

Next, we want to show that every term of type T belongs to R_T. Here, the induction will be on typing derivations (it would be surprising to see a proof about well-typed terms that did not somewhere involve induction on typing derivations!). The only technical dfficulty here is in dealing with the λ-abstraction case. Since we are arguing by induction, the demonstration that a term λx:T₁.t₂belongs to should involve applying the induction hypothesis to show that t₂ belongs to . But is defined to be a set of closed terms, while t₂ may contain x free, so this does not make sense.

This problem is resolved by using a standard trick to suitably generalize the induction hypothesis: instead of proving a statement involving a closed term, we generalize it to cover all closed instances of an open term t.

12.1.5 Lemma

If x₁ ; T₁, ..., x_n : T_n ⊢ t : T and v₁ ..., v_n are closed values of types T₁…T_n with for each i, then R_T([x₁ ↦ v₁] ··· [x_n ↦ v_n]t).

Proof: By induction on a derivation of x₁ : T₁, ..., x_n : T_n ⊢ t : T. (The most interesting case is the one for abstraction.)

Case T-VAR:

t = x_i

T = T_i

Immediate.

Case T-ABS:	t = λx:S1 .s2	x1 : T1, ..., xn : Tn, x:S1 ⊢ s2 : S2
	T = S1 → S2

Obviously, [x₁ ↦ v₁] ··· [x_n ↦ v_n]t evaluates to a value, since it is a value already. What remains to show is that for any s : S₁ such that . So suppose s is such a term. By Lemma 12.1.3, we have s →* v for some v. By Lemma 12.1.4, . Now, by the induction hypothesis, . But

•  

  	(λx:S1 . [x1 ↦ v1] ··· [xn ↦ vn]s2) s
  →*	[x1 ↦ v1] ··· [xn ↦ vn][x ↦ v]s2,

from which Lemma 12.1.4 gives us

that is, . Since s was chosen arbitrarily, the definition of gives us

Case T-APP:	t = t1 t2
	x1 : T1, ..., xn : Tn ⊢ t1 : T11 → T12
	x1 : T1, ..., xn : Tn ⊢ t2 : T11
	T = T12

The induction hypothesis gives us and . By the definition of ,

i.e., ,.

We now obtain the normalization property as a corollary, simply by taking the term t to be closed in Lemma 12.1.5 and then recalling that all the elements of R_T are normalizing, for every T.

12.1.6 Theorem [Normalization]

If ⊢ t : T, then t is normalizable.

Proof: R_T(t) by Lemma 12.1.5; t is therefore normalizable by Lemma 12.1.3.

12.1.7 Exercise [Recommended, ⋆⋆⋆]

Extend the proof technique from this chapter to show that the simply typed lambda-calculus remains normalizing when extended with booleans (Figure 3-1) and products (Figure 11-5).

^[1]The language studied in this chapter is the simply typed lambda-calculus (Figure 9-1) with a single base type A (11-1).

^[2]The sets R_T are sometimes called saturated sets or reducibility candidates.

---