8.3 SafetyProgress Preservation

---

8.3 Safety = Progress + Preservation

The most basic property of this type system or any other is safety (also called soundness): well-typed terms do not "go wrong." We have already chosen how to formalize what it means for a term to go wrong: it means reaching a "stuck state" (Definition 3.5.15) that is not designated as a final value but where the evaluation rules do not tell us what to do next. What we want to know, then, is that well-typed terms do not get stuck. We show this in two steps, commonly known as the progress and preservation theorems.^[3]

• Progress: A well-typed term is not stuck (either it is a value or it can take a step according to the evaluation rules).

• Preservation: If a well-typed term takes a step of evaluation, then the resulting term is also well typed.^[4]

These properties together tell us that a well-typed term can never reach a stuck state during evaluation.

For the proof of the progress theorem, it is convenient to record a couple of facts about the possible shapes of the canonical forms of types Bool and Nat (i.e., the well-typed values of these types).

8.3.1 Lemma [Canonical Forms]

1. If v is a value of type Bool, then v is either true or false.

2. If v is a value of type Nat, then v is a numeric value according to the grammar in Figure 3-2.

Proof: For part (1), according to the grammar in Figures 3-1 and 3-2, values in this language can have four forms: true, false, 0, and succ nv, where nv is a numeric value. The first two cases give us the desired result immediately. The last two cannot occur, since we assumed that v has type Bool and cases 4 and 5 of the inversion lemma tell us that 0 and succ nv can have only type Nat, not Bool. Part (2) is similar.

8.3.2 Theorem [Progress]

Suppose t is a well-typed term (that is, t : T for some T). Then either t is a value or else there is some t′ with t → t′.

Proof: By induction on a derivation of t : T. The T-TRUE, T-FALSE, and T-ZERO cases are immediate, since t in these cases is a value. For the other cases, we argue as follows.

Case T-IF:	t = if t1 then t2 else t3
	t1 : Bool	t2 : T	t3 : T

By the induction hypothesis, either t₁ is a value or else there is some such that . If t₁ is a value, then the canonical forms lemma (8.3.1) assures us that it must be either true or false, in which case either E-IFTRUE or E-IFFALSE applies to t. On the other hand, if , then, by T-IF, t → if then t₂ else t₃.

Case T-Succ:

t = succ t₁

t₁ : Nat

By the induction hypothesis, either t₁ is a value or else there is some such that . If t₁ is a value, then, by the canonical forms lemma, it must be a numeric value, in which case so is t. On the other hand, if , then, by E-SUCC, .

Case T-PRED:

t = pred t₁

t₁ : Nat

By the induction hypothesis, either t₁ is a value or else there is some such that . If t₁ is a value, then, by the canonical forms lemma, it must be a numeric value, i.e., either 0 or succ nv₁ for some nv₁, and one of the rules E-PREDZERO or E-PREDSUCC applies to t. On the other hand, if , then, by E-PRED, .

Case T-ISZERO:

t = iszero t₁

t₁ : Nat

Similar.

The proof that types are preserved by evaluation is also quite straightforward for this system.

8.3.3 Theorem [Preservation]

If t : T and t → t′, then t′ : T.

Proof: By induction on a derivation of t : T. At each step of the induction, we assume that the desired property holds for all subderivations (i.e., that if s : S and s → s′, then s′ : S, whenever s : S is proved by a subderivation of the present one) and proceed by case analysis on the final rule in the derivation. (We show only a subset of the cases; the others are similar.)

Case T-TRUE:

t = true

T = Bool

If the last rule in the derivation is T-TRUE, then we know from the form of this rule that t must be the constant true and T must be Bool. But then t is a value, so it cannot be the case that t → t′ for any t′, and the requirements of the theorem are vacuously satisfied.

Case T-IF:

t = if t₁ then t₂ else t₃

t₁ : Bool

t₂ : T

t₃ : T

If the last rule in the derivation is T-IF, then we know from the form of this rule that t must have the form if t₁ then t₂ else t₃, for some t₁, t₂, and t₃. We must also have subderivations with conclusions t₁ : Bool, t₂ : T, and t₃ : T. Now, looking at the evaluation rules with if on the left-hand side (Figure 3-1), we find that there are three rules by which t → t′ can be derived: E-IFTRUE, E-IFFALSE, and E-IF. We consider each case separately (omitting the E-FALSE case, which is similar to E-TRUE).

•  

  Subcase E-IFTRUE:

  t₁ = true

  t′ = t₂

• If t → t′ is derived using E-IFTRUE, then from the form of this rule we see that t₁ must be true and the resulting term t′ is the second subexpression t₂. This means we are finished, since we know (by the assumptions of the T-IF case) that t₂ : T, which is what we need.

•  

  Subcase E-IF:

  

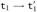
  t′ = if 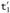then t₂ else t₃

• From the assumptions of the T-IF case, we have a subderivation of the original typing derivation whose conclusion is t₁ : Bool. We can apply the induction hypothesis to this subderivation, obtaining 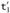: Bool. Combining this with the facts (from the assumptions of the T-IF case) that t₂ : T and t₃ : T, we can apply rule T-IF to conclude that if 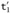then t₂ else t₃ : T, that is t′ : T.

Case T-ZERO:

t = 0

T = Nat

Can't happen (for the same reasons as T-TRUE above).

Case T-SUCC:

t = succ t₁

T = Nat

t₁ : Nat

By inspecting the evaluation rules in Figure 3-2, we see that there is just one rule, E-SUCC, that can be used to derive t → t′. The form of this rule tells us that . Since we also know t₁ : Nat, we can apply the induction hypothesis to obtain , from which we obtain , i.e., t′ : T, by applying rule T-SUCC.

8.3.4 Exercise [⋆⋆ ↛]

Restructure this proof so that it goes by induction on evaluation derivations rather than typing derivations.

The preservation theorem is often called subject reduction (or subject evaluation)-the intuition being that a typing statement t : T can be thought of as a sentence, "t has type T." The term t is the subject of this sentence, and the subject reduction property then says that the truth of the sentence is preserved under reduction of the subject.

Unlike uniqueness of types, which holds in some type systems and not in others, progress and preservation will be basic requirements for all of the type systems that we consider.^[5]

8.3.5 Exercise [⋆]

The evaluation rule E-PREDZERO (Figure 3-2) is a bit counterintuitive: we might feel that it makes more sense for the predecessor of zero to be undefined, rather than being defined to be zero. Can we achieve this simply by removing the rule from the definition of single-step evaluation?

8.3.6 Exercise [⋆⋆, Recommended]

Having seen the subject reduction property, it is reasonable to wonder whether the opposite property-subject expansion-also holds. Is it always the case that, if t → t′ and t′ : T, then t : T? If so, prove it. If not, give a counterexample.

8.3.7 Exercise [Recommended, ⋆⋆]

Suppose our evaluation relation is defined in the big-step style, as in Exercise 3.5.17. How should the intuitive property of type safety be formalized?

8.3.8 Exercise [Recommended, ⋆⋆]

Suppose our evaluation relation is augmented with rules for reducing nonsensical terms to an explicit wrong state, as in Exercise 3.5.16. Now how should type safety be formalized?

The road from untyped to typed universes has been followed many times, in many different fields, and largely for the same reasons.
-Luca Cardelli and Peter Wegner (1985)

^[3]The slogan "safety is progress plus preservation" (using a canonical forms lemma) was articulated by Harper; a variant was proposed by Wright and Felleisen (1994).

^[4]In most of the type systems we will consider, evaluation preserves not only well-typedness but the exact types of terms. In some systems, however, types can change during evaluation. For example, in systems with subtyping (Chapter 15), types can become smaller (more informative) during evaluation.

^[5]There are languages where these properties do not hold, but which can nevertheless be considered to be type-safe. For example, if we formalize the operational semantics of Java in a small-step style (Flatt, Krishnamurthi, and Felleisen, 1998a; Igarashi, Pierce, and Wadler, 1999), type preservation in the form we have given it here fails (see Chapter 19 for details). However, this should be considered an artifact of the formalization, rather than a defect in the language itself, since it disappears, for example, in a big-step presentation of the semantics.

---