29.1 Intuitions

< Free Open Study >

To study functions at the level of types, the first thing we need is some notation for abstraction and application. It is standard practice to use the same notations for these as for abstraction and application at the level of terms, indicating abstraction by λ and application by juxtaposition.^[2] For example, we write λX.{a:X,b:X} for the function that, given a type T, yields the record type {a:T,b:T}. The application of this function to the argument Bool is written (λX.{a:X,b:X}) Bool.

Like ordinary functions, type functions with multiple arguments can be built from one-argument functions by currying. For example, the type expression λY. λZ. "X. (Y→Z→X) → X represents a two-argument function- or, strictly speaking, a one-argument function that, when applied to a type S, yields another one-argument function that, when applied to a type T, yields the type "X.(S→T→X) →X.

We will continue to use informal abbreviations for long type expressions, including type operators. For example, in the remainder of this chapter we will assume we have the abbreviation

   Pair = λY. λZ. "X. (Y→Z→X) →X;

When we write Pair S T in examples, what we really mean is

   (λY. λZ. "X. (Y→Z→X) X) S T.

In other words, we are replacing the informal convention of parametric abbreviation that we have used up to this point with the more elementary informal convention of expanding simple abbreviations to their right-hand sides whenever we see them, plus formal mechanisms for definition and instantiation of type operators. The operations of defining and expanding abbreviations can also be treated formally-i.e., we can make them operations in the object language, instead of conventions in the meta-language-but we will not do so here. Interested readers are referred to the literature on type systems with definitions or singleton kinds; see Severi and Poll (1994), Stone and Harper(2000), Crary (2000), and other works cited there.

Introducing abstraction and application at the level of types gives us the possibility of writing the same type in different ways. For example, if Id is an abbreviation for the type operator λX.X, then the expressions

     Nat → Bool       Nat → Id Bool    Id Nat → Id Bool     Id Nat → Bool    Id (Nat → Bool)  Id (Id (Id Nat → Bool))

are all names for the same arrow type. To make this intuition precise, we introduce a definitional equivalence relation on types, written S ≡ T. The most important clause in the definition of this relation

tells us that a type-level abstraction applied to an argument is equivalent to the body of the abstraction with the argument substituted for the formal parameter. We exploit definitional equivalence in typechecking by a new rule

precisely capturing the intuition that, if two types are equivalent, then the members of one are all members of the other.

Another new possibility that abstraction and application mechanisms give us is the ability to write meaningless type expressions. For example, applying one proper type to another, as in the type expression (Bool Nat), makes n o more sense than applying true to 6 at the term level. To prevent this sort of nonsense, we introduce a system of kinds that classify type expressions according to their arity, just as arrow types tell us about the arities of terms.

Kinds are built from a single atomic kind, written * and pronounced "type," and a single constructor . They include, for example:

*	the kind of proper types (like Bool and Bool→Bool)
⇒	the kind of type operators (i.e., functions from proper types to proper types)
⇒⇒*	the kind of functions from proper types to type operators (i.e., two-argument operators)
(⇒)⇒*	the kind of functions from type operators to proper types

Kinds, then, are "the types of types." In essence, the system of kinds is a copy of the simply typed lambda-calculus, "one level up."

In what follows, we use the word type for any type-level expression-i.e., both for ordinary types like Nat→Nat and "X.X→X and for type operators like λX.X. When we want to focus on ordinary types (i.e., the sorts of type expressions that are actually used to classify terms), we call them proper types.

Type expressions with kinds like (*⇒*)⇒* are called higher-order type operators. Unlike higher-order functions at the term level, which are often extremely useful, higher-order type operators are somewhat esoteric. We will see one class of examples that use them in Chapter 32.

To simplify the problem of checking the well-kindedness of type expressions, we annotate each type-level abstraction with a kind for its bound variable. For example, the official form of the Pair operator is:

   Pair = λA::*. λB::*. "X. (A→B→X) → X;

(Note the doubled colon.) However, since almost all of these annotations will be *, we will continue to write →X.T as an abbreviation for →X::*.T.

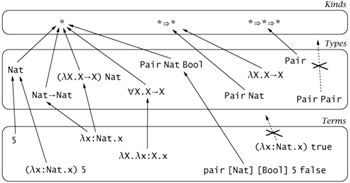
A few pictures may help clarify. The expressions of our language are now divided into three separate classes: terms, types, and kinds. The level of terms contains basic data values (integers, floats), compound data values (records, etc.), value-level abstractions, applications, type abstractions, and type applications.

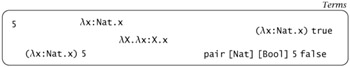
The level of types contains two sorts of expressions. First, there are proper types like Nat, Nat→Nat, Pair Nat Bool, and "X.X→X, which are inhabited by terms. (Of course, not all terms have a type; for example (→x:Nat.x) true does not.)

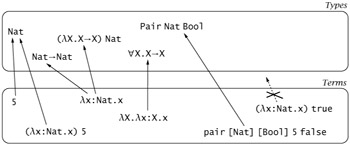
Then there are type operators like Pair and λX.X→X, which do not themselves classify terms (it does not make sense to ask "What terms have type λX.X→X?"), but which can be applied to type arguments to form proper types like (λX.X→X)Nat that do classify terms.

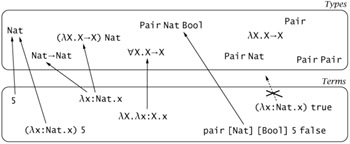
Note that proper types-i.e., type expressions of kind *-may include type operators of higher kinds as subphrases, as in (λX.X→X) Nat or Pair Nat Bool, just as term expressions belonging to base types like Nat may include lambdaabstractions as subexpressions, as in (λx:Nat.x) 5.

Finally, we have the level of kinds. The simplest kind is *, which has all proper types as members.

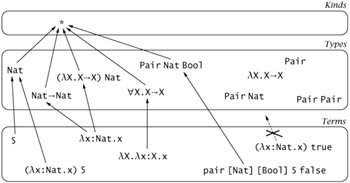
Type operators like λX.X→X and Pair belong to arrow kinds like *⇒* and *⇒*⇒*. Ill-formed type-level expressions, like Pair Pair, do not belong to any kind.

29.1.1 Exercise [⋆]

What is the difference in meaning between the type-level expressions "X.X→X and λX.X→X?

29.1.2 Exercise [⋆]

Why doesn't an arrow type like Nat→Nat have an arrow kind like *⇒*?

A natural question at this point is "Why stop at three levels of expressions?" Couldn't we go on to introduce functions from kinds to kinds, application at the level of kinds, etc., add a fourth level to classify kind expressions according to their functionality, and continue on in this way ad infinitum? Such systems have been investigated by the pure type systems community (Terlouw, 1989; Berardi, 1988; Barendregt, 1991, 1992; Jutting, McKinna, and Pollack, 1994; McKinna and Pollack, 1993; Pollack, 1994). For programming languages, however, three levels have proved sufficient.

Indeed, while type operators can be found, in some form, in essentially all statically typed programming languages, it is relatively rare for language designers to offer programmers even the full power of the present formulation. Some languages (e.g., Java) offer only a few built-in type operators like Array, with no facilities for defining new ones. Others bundle type operators together with other language features; in ML, for example, type operators are provided as part of the datatype mechanism; we can define parametric datatypes like^[3]

   type 'a tyop = Tyoptag of ('a → 'a);   type 'a Tyop = tyoptag of ('a → 'a);

which we would write as

   Tyop = λX. <tyoptag:X→X>;

In other words, in ML we can define parametric variants, but not arbitrary parametric types. The benefit of this restriction is that, wherever the type operator Tyop appears in a program at the level of types, the corresponding tag tyoptag will appear at the level of terms-that is, every place where the typechecker needs to use the definitional equivalence relation to replace a type like Tyop Nat by its reduced form Nat→Nat will be marked in the program by an explicit occurrence of tyoptag. This substantially simplifies the typechecking algorithm.^[4]

The ⇒ constructor on kinds is the only one that we have space to discuss here, but a great many others have been studied; indeed, the range of kinding systems for checking and tracking various properties of type expressions rivals the range of type systems for analyzing properties of terms. There are record kinds (whose elements are records of types-not to be confused with the types of records; they offer a natural way of defining systems of mutually recursive types), row kinds (which describe "rows of fields" that can be used to assemble record types in systems with row variable polymorphism-see page 337), power kinds or power types (which offer an alternate presentation of subtyping-see Cardelli, 1988a), singleton kinds (related to definitions-see page 441-and to module systems with sharing-see page 465), dependent kinds (an analog "one level up" of the dependent types discussed in §30.5),and many more.

^[2]The one drawback of this notational parsimony is that the terminology for different sorts of expressions can become a little contorted. In particular, the phrase "type abstraction" might now mean an abstraction that expects a type as its argument (i.e., a term like λX.t), or it might equally mean an abstraction at the level of types (i.e., a type expression like λX.{a:X}). In contexts where both are possible, people tend to use "polymorphic function" for the first sense and "type-level abstraction" or "operator abstraction" for the second.

^[3]We're ignoring ML's conventions for capitalization of identifiers for the sake of the example. In OCaml, this definition would really be written

^[4]This restriction is similar to ML's treatment of recursive types, discussed in §20-1. The bundling of recursive types into datatype definitions gives the programmer the convenience of equi-recursive types and the typechecker the simplicity of iso-recursive types by hiding the fold/unfold annotations in the tagging and case analysis operations associated with variant types.

< Free Open Study >