28.7 Bounded Existentials

---

28.7 Bounded Existentials

To extend the kernel F_<: typechecking algorithm to a language with existential types, we must deal with one additional subtlety. Recall the declarative elimination rule for existentials:

In §24-1 we remarked that the type variable X appears in the context in which t₂'s type is calculated in the second premise but not in the context of the rule's conclusion. This means that the type T₂ must not contain X free, since any free occurrences of X will be out of scope in the conclusion. This point was discussed in more detail in §25.5, where we observed that the change in the context from premise t o conclusion corresponds to anegative shift of variable indices in T₂, when we represent types in the nameless deBruijn format; this shift will fail if T₂ happens to contain X free.

What are the implications of this observation for a minimal typing algorithm for a language with existentials? In particular, what should we do with an expression like t = let {X,x} = p in x, where p has type {$X,Nat→X}? The most natural type of the body x is Nat→X, which mentions the bound variable X. However, according to the declarative typing relation (with the subsumption rule), x also has the types Nat→Top and Top. Since neither of these mentions X, the whole term t can legally be assigned the types Nat→Top and Top in the declarative system. More generally, we are always free to promote the body of an unpacking expression to any type that does not involve the bound type variable X and then apply T-UNPACK. So, if we want our minimal typing algorithm to be complete, it should not simply fail when it encounters an unpacking expression where the minimal type T₂ of the body contains a free occurrence of the bound variable X. Instead, it should try to promote T₂ to some supertype that does not mention X. The key observation that we need to make this work is that the set of X-free supertypes of a given type always has a minimal element, as the following exercise (whose solution is due to Ghelli and Pierce, 1998) shows.

28.7.1 Exercise [⋆⋆⋆]:

Give an algorithm for calculating, in kernel F_<: with bounded existentials, the minimal X-free supertype of a given type T with respect to a context Г, written R_x,_Г(T).

The algorithmic typing rule for existential elimination can now be written like this:

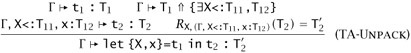
For full F_<: with bounded existentials, the situation is more problematic, as might be expected. Ghelli and Pierce (1998) give an example of a type T, a context Г, and a variable X such that the set of X-free supertypes T under Г has no minimal element. It immediately follows that the typing relation for this system lacks minimal types.

28.7.2 Exercise [⋆⋆⋆]:

Show that the subtyping relation for a variant of full F_<: with just bounded existential types (no universal types) is also undecidable.

---