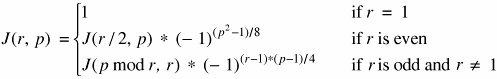Section 12.3. Public Key Encryption Systems
12.3. Public Key Encryption SystemsIn 1976, Diffie and Hellman [DIF76] proposed a new kind of system, public key encryption, in which each user would have a key that did not have to be kept secret. Counterintuitively, the public nature of the key would not inhibit the system's secrecy. The public key transformation is essentially a one-way encryption with a secret (private) way to decrypt. Public key systems have an enormous advantage over conventional key systems: Anyone can send a secret message to a user, while the message remains adequately protected from being read by an interceptor. With a conventional key system, a separate key is needed for each pair of users. As we have seen, n users require n * (n - 1)/2 keys. As the number of users grows, the number of keys rapidly increases. Determining and distributing these keys is a problem; more serious is maintaining security for the keys already distributed, because we cannot expect users to memorize so many keys. CharacteristicsWith a public key or asymmetric encryption system, each user has two keys: a public key and a private key. The user may publish the public key freely. The keys operate as inverses. Let kPRIV be a user's private key, and let kPUB be the corresponding public key. Then, P = D(kPRIV, E(kPUB,P)) That is, a user can decode with a private key what someone else has encrypted with the corresponding public key. Furthermore, with the second public key encryption algorithm, P = D(kPUB, E(kPRIV, P) a user can encrypt a message with a private key and the message can be revealed only with the corresponding public key. (We study an application of this second case later in this chapter, when we examine digital signature protocols.) These two properties imply that public and private keys can be applied in either order. Ideally, the decryption function D can be applied to any argument, so we can decrypt first and then encrypt. With conventional encryption, one seldom thinks of decrypting before encrypting. With public keys, it simply means applying the private transformation first, and then the public one. We saw in Chapter 2 that, with public keys, only two keys are needed per user: one public and one private. Thus, users B, C, and D can all encrypt messages for A, using A's public key. If B has encrypted a message using A's public key, C cannot decrypt it, even if C knew it was encrypted with A's public key. Applying A's public key twice, for example, would not decrypt the message. (We assume, of course, that A's private key remains secret.) In the remainder of this section, we look closely at three types of public key systems: MerkleHellman knapsacks, RSA encryption, and El Gamal applied to digital signatures. MerkleHellman KnapsacksMerkle and Hellman [MER78b] developed an encryption algorithm based on the knapsack problem described earlier. The knapsack problem presents a set of positive integers and a target sum, with the goal of finding a subset of the integers that sum to the target. The knapsack problem is NP-complete, implying that to solve it probably requires time exponential in the size of the problemin this case, the number of integers. We present MerkleHellman in two steps, to aid understanding. First we outline the operation of the MerkleHellman knapsack encryption method. Then we revisit the technique in more detail. Introduction to MerkleHellman KnapsacksThe idea behind the MerkleHellman knapsack scheme is to encode a binary message as a solution to a knapsack problem, reducing the ciphertext to the target sum obtained by adding terms corresponding to 1s in the plaintext. That is, we convert blocks of plaintext to a knapsack sum by adding into the sum those terms that match with 1 bits in the plaintext, as shown in Figure 12-14.
A knapsack is represented as a vector of integer terms in which the order of the terms is important. There are actually two knapsacksan easy one, to which a fast (linear time) algorithm exists, and a hard one, derived by modifying the elements of the easy knapsack. The modification is such that a solution with the elements of either knapsack is a solution for the other one as well. This modification is a trapdoor, permitting legitimate users to solve the problem simply. Thus, the general problem is NP-complete, but a restricted version of it has a very fast solution. The algorithm begins with a knapsack set, each of whose elements is larger than the sum of all previous elements. Suppose we have a sequence where each element ak is larger than a1 + a2 +…+ ak-1. If a sum is between ak and ak+1, it must contain ak as a term, because no combination of the values a1, a2,…, ak-1 could produce a total as large as ak. Similarly, if a sum is less than ak, clearly it cannot contain ak as a term. The modification of the algorithm disguises the elements of the easy knapsack set by changing this increasing-size property in a way that preserves the underlying solution. The modification is accomplished with multiplication by a constant mod n. Detailed Explanation of the MerkleHellman TechniqueThis detailed explanation of MerkleHellman is intended for people who want a deeper understanding of the algorithm. General KnapsacksThe knapsack problem examines a sequence a1, a2, …, an of integers and a target sum, T. The problem is to find a vector of 0s and 1s such that the sum of the integers associated with 1s equals T. That is, given S = [a1,a2, …, an], and T, find a vector V of 0s and 1s such that For example, consider the list of integers [17,38,73,4,11,1] and the target number 53. The problem is to find which of the integers to select for the sum, that is, which should correspond with 1s in V. Clearly 73 cannot be a term, so we can ignore it. Trying 17, the problem reduces to finding a sum for (53 - 17 = 36). With a second target of 36, 38 cannot contribute, and 4 + 11 + 1 are not enough to make 36. We then conclude that 17 is not a term in the solution. If 38 is in the solution, then the problem reduces to the new target (53 - 38 = 15). With this target, a quick glance at the remaining values shows that 4 and 11 complete the solution, since 4 + 11 = 15. A solution is thus 38 + 4 + 11. This solution proceeded in an orderly manner. We considered each integer as possibly contributing to the sum, and we reduced the problem correspondingly. When one solution did not produce the desired sum, we backed up, discarding recent guesses and trying alternatives. This backtracking seriously impaired the speed of solution. With only six integers, it did not take long to determine the solution. Fortunately, we discarded one of the integers (73) immediately as too large, and in a subproblem we could dismiss another integer (38) immediately. With many integers, it would have been much more difficult to find a solution, especially if they were all of similar magnitude so that we could not dismiss any immediately. Superincreasing KnapsacksSuppose we place an additional restriction on the problem: The integers of S must form a superincreasing sequence, that is, one where each integer is greater than the sum of all preceding integers. Then, every integer ak would be of the form In the previous example, [1,4,11,17,38,73] is a superincreasing sequence. If we restrict the knapsack problem to superincreasing sequences, we can easily tell whether a term is included in the sum or not. No combination of terms less than a particular term can yield a sum as large as the term. For instance, 17 is greater than 1 + 4 + 11 (=16). If a target sum is greater than or equal to 17, then 17 or some larger term must be a term in the solution. The solution of a superincreasing knapsack (also called a simple knapsack) is easy to find. Start with T. Compare the largest integer in S to it. If this integer is larger than T, it is not in the sum, so let the corresponding position in V be 0. If the largest integer is less than or equal to T, that integer is in the sum, so let the corresponding position in V be 1 and reduce T by the integer. Repeat for all remaining integers in S. An example solving a simple knapsack for targets 96 and 95 is shown in Figure 12-15.
The Knapsack Problem as a Public Key Cryptographic AlgorithmThe MerkleHellman encryption technique is a public key cryptosystem. That is, each user has a public key, which can be distributed to anyone, and a private key, which is kept secret. The public key is the set of integers of a knapsack problem (not a superincreasing knapsack); the private key is a corresponding superincreasing knapsack. The contribution of Merkle and Hellman was the design of a technique for converting a superincreasing knapsack into a regular one. The trick is to change the numbers in a nonobvious but reversible way. Modular Arithmetic and KnapsacksIn normal arithmetic, adding to or multiplying a superincreasing sequence preserves its superincreasing nature, so the result is still a superincreasing sequence. That is, if a > b then k * a > k * b for any positive integer k. However, in arithmetic mod n, the product of two large numbers may in fact be smaller than the product of two small numbers, since results larger than n are reduced to between 0 and n-1. Thus, the superincreasing property of a sequence may be destroyed by multiplication by a constant mod n. To see why, consider a system mod 11. The product 3 * 7 mod 11 = 21 mod 11 = 10, while 3 * 8 mod 11 = 24 mod 11 = 2. Thus, even though 7 < 8, we find that 3 * 7 mod 11 > 3 * 8 mod 11. Multiplying a sequence of integers mod some base may destroy the superincreasing nature of the sequence. Modular arithmetic is sensitive to common factors. If all products of all integers are mapped into the space of the integers mod n, clearly there will be some duplicates; that is, two different products can produce the same result mod n. For example, if w * x mod n = r, then w * x + n mod n = r, w * x + 2n mod n = r, and so on. Furthermore, if w and n have a factor in common, then not every integer between 0 and n-1 will be a result of w * x mod n for some x. For instance, look at the integers mod 5. If w = 3 and x = 1, 2, 3,…, the multiplication of x * w mod 5 produces all the results from 0 to 4, as shown in Table 12-13. Notice that after x = 5, the modular results repeat.
However, if we choose w = 3 and n = 6, not every integer between 0 and 5 is used. This occurs because w and n share the common factor 3. Table 12-14 shows the results of 3 * x mod 6. Thus, there may be some values that cannot be written as the product of two integers mod n for certain values of n. For all values between 0 and n-1 to be produced, n must be relatively prime to w (that is, they share no common factors with each other).
If w and n are relatively prime, w has a multiplicative inverse mod n. That means that for every integer w, there is another integer w-1 such that w * w-1 = 1 mod n. A multiplicative inverse undoes the effect of multiplication: (w * q) * w-1 = q. (Remember that multiplication is commutative and associative in the group mod n, so that w * q * w-1 = (w * w-1) * q = q mod n.) With these results from modular arithmetic, Merkle and Hellman found a way to break the superincreasing nature of a sequence of integers. We can break the pattern by multiplying all integers by a constant w and taking the result mod n where w and n are relatively prime. Transforming a Superincreasing KnapsackTo perform an encryption using the MerkleHellman algorithm, we need a superincreasing knapsack that we can transform into what is called a hard knapsack. In this section we show you just how to do that. We begin by picking a superincreasing sequence S of m integers. Such a sequence is easy to find. Select an initial integer (probably a relatively small one). Choose the next integer to be larger than the first. Then select an integer larger than the sum of the first two. Continue this process by choosing new integers larger than the sum of all integers already selected. For example,
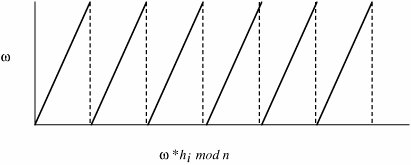
is such a sequence. The superincreasing sequence just selected is called a simple knapsack. Any instance of the knapsack problem formed from that knapsack has a solution that is easy to find. After selecting a simple knapsack S = [s1, s2,…,sm], we choose a multiplier w and a modulus n. The modulus should be a number greater than the sum of all si. The multiplier should have no common factors with the modulus. One easy way to guarantee this property is to choose a modulus that is a prime number, since no number smaller than it will have any common factors with it. Finally, we replace every integer si in the simple knapsack with the term hi = w * si mod n Then, H = [h1, h2,…, hm] is a hard knapsack. We use both the hard and simple knapsacks in the encryption. For example, start with the superincreasing knapsack S = [1, 2, 4, 9] and transform it by multiplying by w and reducing mod n where w = 15 and n = 17. 1 * 15 = 15 mod 17 = 15 2 * 15 = 30 mod 17 = 13 4 * 15 = 60 mod 17 = 9 9 * 15 = 135 mod 17 = 16 The hard knapsack derived in this example is H = [15, 13, 9, 16]. Example Using MerkleHellman KnapsacksLet us look at how to use MerkleHellman encryption on a plaintext message P. The encryption algorithm using MerkleHellman knapsacks begins with a binary message. That is, the message is envisioned as a binary sequence P = [p1, p2,…, pk]. Divide the message into blocks of m bits, P0 = [pl, p2,…, pm], P1 = [pm+1,…, p2m], and so forth. The value of m is the number of terms in the simple or hard knapsack. The encipherment of message P is a sequence of targets, where each target is the sum of some of the terms of the hard knapsack H. The terms selected are those corresponding to 1 bits in Pi so that Pi serves as a selection vector for the elements of H. Each term of the ciphertext is Pi * H, the target derived using block Pi as the selection vector. For this example, we use the knapsacks S = [1, 2, 4, 9] and H = [15, 13, 9, 16] obtained in the previous section. With those knapsacks, w = 15, n = 17, and m = 4. The public key (knapsack) is H, while S is kept secret. The message P = 0100101110100101 is encoded with the knapsack H = [15, 13, 9,16] as follows. P = 0100 1011 1010 0101 [0, 1, 0, 0] * [15, 13, 9, 16] = 13 [1, 0, 1, 1] * [15, 13, 9, 16] = 40 [1, 0, 1, 0] * [15, 13, 9, 16] = 24 [0, 1, 0, 1] * [15, 13, 9, 16] = 40 The message is encrypted as the integers 13, 40, 24, 29, using the public knapsack H = [15, 13, 9, 16]. Knapsack Decryption AlgorithmThe legitimate recipient knows the simple knapsack and the values of w and n that transformed it to a hard public knapsack. The legitimate recipient determines the value w-1 so that w * w-1 = 1 mod n. In our example, 15 * 1 mod 17 is 8, since 15 * 8 mod 17 = 120 mod 17 = (17 * 7) + 1 mod 17 = 1. Remember that H is the hard knapsack derived from the simple knapsack S. H is obtained from S by H = w * S mod n (This notation, in which a constant is multiplied by a sequence, should be interpreted as hi = w * si mod n for all i, 1 C = H * P = w * s * P mod n To decipher, multiply C by w-1, since w-1 * C = w-1 * H * P = w-1 * w * S * P = S * P mod n To recover the plaintext message P, the legitimate recipient would solve the simple knapsack problem with knapsack S and target w-1 * Ci for each ciphertext integer Ci. Since w-1 * Ci = S * P mod n, the solution for target w-1 * Ci is plaintext block Pi, which is the message originally encrypted. Example of DecryptionWe continue our example, in which the underlying simple knapsack was S = [1, 2, 4, 9], with w = 15 and n = 17. The transmitted messages were 13, 40, 24, and 29. To decipher, we multiply these messages by 8 mod 17 because 8 is 15-1 mod 17. Then we can easily solve the simple knapsacks, as shown here: 13 * 8 = 104 mod 17 = 2 = [0100] 40 * 8 = 320 mod 17 = 14 = [1011] 24 * 8 = 192 mod 17 = 5 = [1010] 29 * 8 = 232 mod 17 = 11 = [0101] The recovered message is thus 0100101110100101. Cryptanalysis of the Knapsack AlgorithmIn this example, because m is 4, we can readily determine the solution to the knapsack problem for 13, 40, 24, and 29. Longer knapsacks (larger values of m), which also imply larger values of the modulus n, are not so simple to solve. Typically, you want to choose the value of n to be 100 to 200 binary digits long. If n is 200 bits long, the si are usually chosen to be about 2200 apart. That is, there are about 200 terms in the knapsacks, and each term of the simple knapsack is between 200 and 400 binary digits long. More precisely, s0 is chosen so that 1 You can use a sequence of m random numbers, r1, r2, r3,…, rm to generate the simple knapsack just described. Each ri must be between 0 and 2200. Then each value si of the simple knapsack is determined as si = 2200+i-1 + ri for i = 1, 2,…, m. With such large terms for S (and H), it is infeasible to try all possible values of si to infer S given H and C. Even assuming a machine could do one operation every microsecond, it would still take 1047 years to try every one of the 2200 choices for each si. A massively parallel machine with 1000 or even 1,000,000 parallel elements would not reduce this work factor enough to weaken the encryption. Weaknesses of the MerkleHellman Encryption AlgorithmThe MerkleHellman knapsack method seems secure. With appropriately large values for n and m, the chances of someone's being able to crack the method by brute force attack are slim. However, an interceptor does not have to solve the basic knapsack problem to break the encryption, since the encryption depends on specially selected instances of the problem. In 1980, Shamir found that if the value of the modulus n is known, it may be possible to determine the simple knapsack. The exact method is beyond the scope of this book, but we can outline the method of attack. For more information, see the articles by Shamir and Zippel [SHA80] and Adleman [ADL83]. First, notice that since all elements of the hard knapsack are known, you can readily determine which elements correspond to which elements of the simple knapsack. Consider h0 and h1, the first two elements of a hard knapsack, corresponding to simple knapsack elements s0 and s1. Let ρ= h0/h1 mod n Since h0 = w * s0 mod n and h1 = w * s1 mod n, it is also true that ρ = (w * s0)/(w * s1) = s0/s1 mod n Given the ratio ρ, determine the sequence Δ = ρ mod n, 2 * ρ mod n 3 * ρ mod n, …, k * ρ mod n, …, 2m * ρ mod n For some k, k and sl will cancel each other mod n; that is, k * (1/s1) = 1 mod n. Then k * ρ mod n = k * s0 * 1/s1 mod n = so mod n = s0 It is reasonable to expect that s0 will be the smallest element of Δ. Once s0 is known, determining w, then w-1 and each of the si are not hard. A more serious flaw was identified later by Shamir [SHA82]. The actual argument is also beyond the scope of this book, but again it can be sketched fairly briefly. The approach tries to deduce w and n from the hi alone. The approximate size of n can be deduced from the fact that it will be longer than any of the hi since they have been reduced mod n; however, n will not be substantially longer than the longest hi, since it is likely that the results after taking the modulus will be fairly evenly distributed between 1 and n. Assume you are trying to guess w. You might iteratively try different candidate values ω= 1, 2, 3, . . . for w. The graph of ω * hi mod n as a function of ω would increase steadily until a value of ω * hi was greater than n. At that point, the graph of ω * hi would be discontinuous and have a small value. The values of ω * hi would then resume their steady increase as ω increased until ω * hi exceeded n again. The graph would form a progression of jagged peaks, resembling the teeth of a saw. The slope of each "tooth" of the graph is hi. Figure 12-16 displays a graphical representation of this process. Figure 12-16. Graph of Change of MerkleHellman Knapsack Function. The correct value of ω = w occurs at one of the points of discontinuity of the graph of ω * hi mod n. This same pattern occurs for all values hi: h1, h2, and so forth. Since ω is a discontinuity point of ω * h1 mod n, it is also a discontinuity of ω * h2 mod n, of ω * h3 mod n, and so forth. To determine ω superimpose the graph of ω * h1 mod n on ω * h2 mod n, superimpose those graphs on ω * h3 mod n, and so on. Then, w will be at one of the places where all of the curves are discontinuous and fall from a high value to a low one. Two such graphs are shown in Figure 12-17. The problem of determining w is thus reduced to finding the point at which all of these discontinuities coincide. Figure 12-17. Coinciding Discontinuities. The actual process is a little more difficult. The value of n has been replaced by real number N. Since n and N are unknown, the graphs are scaled by dividing by N and then approximating by successive values of the real number ω/N in the function (ω/N) * hi mod 1.0. Fortunately, this reduces to the solution of a system of simultaneous linear inequalities. That problem can be solved in polynomial time. Therefore, the Merkle Hellman knapsack problem can be broken in reasonable time. Notice that this solution does not apply to the general knapsack problem; it applies only to the special class of knapsack problems derived from superincreasing sequences by multiplication by a constant modulo another constant. Thus, the basic knapsack problem is intact; only this restricted form has been solved. This result underscores the point that a cryptosystem based on a hard problem is not necessarily as hard to break as the underlying problem. Since it has become known that the MerkleHellman knapsack can be broken, other workers have analyzed variations of MerkleHellman knapsacks. (See, for example, [BRI83] and [LAG83].) To date, transformed knapsacks do not seem secure enough for an application where a concerted attack can be expected. The MerkleHellman algorithm or a variation would suffice for certain low-risk applications. However, because the MerkleHellman method is fairly complicated to use, it is not often recommended. RivestShamirAdelman (RSA) EncryptionThe RSA algorithm is another cryptosystem based on an underlying hard problem. This algorithm was introduced in 1978 by Rivest, Shamir, and Adelman [RIV78]. As with the MerkleHellman algorithm, RSA has been the subject of extensive cryptanalysis. No serious flaws have yet been foundnot a guarantee of its security but suggesting a high degree of confidence in its use. In this section, we present the RSA algorithm in two parts. First, we outline RSA, to give you an idea of how it works relative to the other algorithms we have studied. Then, we delve more deeply into a detailed analysis of the steps involved. Introduction to the RSA AlgorithmOn the surface, the RSA algorithm is similar to the MerkleHellman method, in that solving the encryption amounts to finding terms that add to a particular sum or multiply to a particular product. The RSA encryption algorithm incorporates results from number theory, combined with the difficulty of determining the prime factors of a target. The RSA algorithm also operates with arithmetic mod n. Two keys, d and e, are used for decryption and encryption. They are actually interchangeable. (The keys for MerkleHellman were not interchangeable.) The plaintext block P is encrypted as Pe mod n. Because the exponentiation is performed mod n, factoring Pe to uncover the encrypted plaintext is difficult. However, the decrypting key d is carefully chosen so that (Pe)d mod n = P. Thus, the legitimate receiver who knows d simply computes (Pe)d mod n = P and recovers P without having to factor Pe. The encryption algorithm is based on the underlying problem of factoring large numbers. The factorization problem is not known or even believed to be NP-complete; the fastest known algorithm is exponential in time. Detailed Description of the Encryption AlgorithmThe RSA algorithm uses two keys, d and e, which work in pairs, for decryption and encryption, respectively. A plaintext message P is encrypted to ciphertext C by C = Pe mod n The plaintext is recovered by P = Cd mod n Because of symmetry in modular arithmetic, encryption and decryption are mutual inverses and commutative. Therefore, P = Cd mod n = (Pe)d mod n = (Pd)e mod n This relationship means that one can apply the encrypting transformation and then the decrypting one, or the decrypting one followed by the encrypting one. Key ChoiceThe encryption key consists of the pair of integers (e, n), and the decryption key is (d, n). The starting point in finding keys for this algorithm is selection of a value for n. The value of n should be quite large, a product of two primes p and q. Both p and q should be large themselves. Typically, p and q are nearly 100 digits each, so n is approximately 200 decimal digits (about 512 bits) long; depending on the application, 768, 1024, or more bits may be more appropriate. A large value of n effectively inhibits factoring n to infer p and q. Next, a relatively large integer e is chosen so that e is relatively prime to (p - 1) * (q - 1). (Recall that "relatively prime" means that e has no factors in common with (p - 1) * (q - 1).) An easy way to guarantee that e is relatively prime to (p - 1) * (q - 1) is to choose e as a prime that is larger than both (p - 1) and (q - 1). Finally, select d such that e * d = 1 mod (P - 1) * (q - 1) Mathematical Foundations of the RSA AlgorithmThe Euler totient function φ(n) is the number of positive integers less than n that are relatively prime to n. If p is prime, then φ(p) = p - 1 Furthermore, if n = p * q, where p and q are both prime, then φ(n) = φ(p) * φ(q) = (p - 1) * (q - 1) Euler and Fermat proved that xφ(n) Suppose we encrypt a plaintext message P by the RSA algorithm so that E(P) = Pe. We need to be sure we can recover the message. The value e is selected so that we can easily find its inverse d. Because e and d are inverses mod φ(n), e * d e * d = k * φ(n) +1 (*) for some integer k. Because of the EulerFermat result, assuming P and p are relatively prime, Pp-1 pk*φ(n) pk*φ(n)+1 The same argument holds for q, so pk*φ(n)+1 Combining these last two results with (*) produces
so that (Ped and e and d are inverse operations. ExampleLet p = 11 and q = 13, so that n = p * q = 143 and φ(n) = (p - 1) * (q - 1) = 10 * 12 = 120. Next, an integer e is needed, and e must be relatively prime to (p - 1) * (q - 1). Choose e = 11. The inverse of 11 mod 120 is also 11, since 11 * 11 = 121 = 1 mod 120. Thus, both encryption and decryption keys are the same: e = d = 11. (For the example, e = d is not a problem, but in a real application you would want to choose values where e is not equal to d.) Let P be a "message" to be encrypted. For this example we use P = 7. The message is encrypted as follows: 711 mod 143 = 106, so that E(7) = 106. (Note: This result can be computed fairly easily with the use of a common pocket calculator. 711 = 79 * 72. Then 79 = 40 353 607, but we do not have to work with figures that large. Because of the reducibility rule, a * b mod n = (a mod n) * (b mod n) mod n. Since we will reduce our final result mod 143, we can reduce any term, such as 79, which is 8 mod 143. Then, 8 * 72 mod 143 = 392 mod 143 = 106.) This answer is correct since D(106) = 10611 mod 143 = 7. Use of the AlgorithmThe user of the RSA algorithm chooses primes p and q, from which the value n = p * q is obtained. Next e is chosen to be relatively prime to (p - 1) * (q - 1); e is usually a prime larger than (p - 1) or (q - 1). Finally, d is computed as the inverse of e mod (φ(n)). The user distributes e and n and keeps d secret; p, q, and φ(n) may be discarded (but not revealed) at this point. Notice that even though n is known to be the product of two primes, if they are relatively large (such as 100 digits long), it will not be feasible to determine the primes p and q or the private key d from e. Therefore, this scheme provides adequate security for d. It is not even practical to verify that p and q themselves are primes, since that would require considering on the order of 1050 possible factors. A heuristic algorithm from Solovay and Strassen [SOL77] can determine the probability of primality to any desired degree of confidence. Every prime number passes two tests. If p is prime and r is any number less than p, then gcd(P,r) = 1 (where gcd is the greatest common divisor function) and j(r,p) where J(r,p) is the Jacobi function defined as follows. If a number is suspected to be prime but fails either of these tests, it is definitely not a prime. If a number is suspected to be a prime and passes both of these tests, the likelihood that it is prime is at least 1/2. The problem relative to the RSA algorithm is to find two large primes p and q. With the Solovay and Strassen approach, you first guess a large candidate prime p. You then generate a random number r and compute gcd(p,r) and J(r,p). If either of these tests fails, p was not a prime, and you stop the procedure. If both pass, the likelihood that p was not prime is at most 1/2. The process repeats with a new value for r chosen at random. If this second r passes, the likelihood that a nonprime p could pass both tests is at most 1/4. In general, after the process is repeated k times without either test failing, the likelihood that p is not a prime is at most 1/2k. Zimmerman [ZIM86] gives a method for computing RSA encryptions efficiently. Cryptanalysis of the RSA MethodLike the MerkleHellman knapsack algorithm, the RSA method has been scrutinized intensely by professionals in computer security and cryptanalysis. Several minor problems have been identified with it, but there have been no flaws as serious as those for the MerkleHellman method. Boneh [BON99] catalogs known attacks on RSA. He notes no successful attacks on RSA itself, but several serious but improbable attacks on implementation and use of RSA. Cryptographic ChallengesAs it has done for symmetric encryption, RSA has set challenges for RSA encryption. (See http://www.rsasecurity.com/rsalabs/node.asp?id=2093 for more details.) These challenges involve finding the two prime factors of a composite number of a particular size. These numbers are identified by their size in decimal digits or bits. (For very rough approximations, three bits are close to one decimal digit.) The first challenges (using decimal digit lengths) were RSA-140, -155, -160, and -200. Then using bit lengths, the challenges were RSA-576, -640, -704, -768, and so on. RSA-200, the last number in the decimal series, is 663 bits long, so its difficulty fits between RSA-640 and RSA-704. Numbers through RSA-200 have been factored. The first, RSA-140, was factored in 1999 in 1 month using approximately 200 machines. RSA-155, a 512-bit number, was factored in 1999 in approximately 3.7 months using 300 machines, but RSA-160 was factored in 2003 in only 20 days. (It is believed that improvements in hardware were significant in that time reduction.) The most recent, RSA-200, was factored in 2005 [RSA05] after about 18 calendar months of elapsed time, using an unspecified number of machines. As with the symmetric key challenges, these are not just academic exercises. They give a good indication of the state of the art in factoring and hence the sizes of numbers known to be factorable (and hence weak choices for key lengths). For most encryption an attacker would not be able to covertly assemble the number of high performance machines needed to factor a number quickly. Thus, 512 bits is probably too small for all but the least important uses, but slightly above that, 600 to 700 bits requires months for a dedicated network to crack. A key of about 768 bits is probably satisfactory for routine uses now, and a 1024-bit key will likely withstand very diligent attacks for some time. The El Gamal and Digital Signature AlgorithmsAnother public key algorithm was devised in 1984 by El Gamal [ELG85, ELG86]. While this algorithm is not widely used directly, it is of considerable importance in the U.S. Digital Signature Standard (DSS) [NIS92b, NIS94] of the National Institute of Standards and Technology (NIST). This algorithm relies on the difficulty of computing discrete logarithms over finite fields. Because it is based on arithmetic in finite fields, as is RSA, it bears some similarity to RSA. We investigated digital signatures in Chapter 2. Recall that a digital signature is, like a handwritten signature, a means of associating a mark unique to an individual with a body of text. The mark should be unforgeable, meaning that only the originator should be able to compute the signature value. But the mark should be verifiable, meaning that others should be able to check that the signature comes from the claimed originator. The general way of computing digital signatures is with public key encryption; the signer computes a signature value by using a private key, and others can use the public key to verify that the signature came from the corresponding private key. El Gamal AlgorithmIn the El Gamal algorithm, to generate a key pair, first choose a prime p and two integers, a and x, such that a < p and x < p and calculate y = ax mod p. The prime p should be chosen so that (p - 1) has a large prime factor, q. The private key is x and the public key is y, along with parameters p and a. To sign a message m, choose a random integer k, 0 < k < p - 1, which has not been used before and which is relatively prime to (p - 1), and compute r = ak mod p and s = k-1 (m - xr) mod (p - 1) where k-1 is the multiplicative inverse of k mod (p - 1), so that k * k-1 = 1 mod (p - 1). The message signature is then r and s. A recipient can use the public key y to compute yr rs mod p and determine that it is equivalent to am mod p. To defeat this encryption and infer the values of x and k given r, s, and m, the intruder could find a means of computing a discrete logarithm to solve y = ax and r = ak. Digital Signature AlgorithmThe U.S. Digital Signature Algorithm (DSA) (also called the Digital Signature Standard or DSS) [NIS94] is the El Gamal algorithm with a few restrictions. First, the size of p is specifically fixed at 2511 < p < 2512 (so that p is roughly 170 decimal digits long). Second, q, the large prime factor of (p - 1) is chosen so that 2159 < q < 2160. The algorithm explicitly uses H(m), a hash value, instead of the full message text m. Finally, the computations of r and s are taken mod q. Largely, one can argue that these changes make the algorithm easy to use for those who do not want or need to understand the underlying mathematics. However, they also weaken the potential strength of the encryption by reducing the uncertainty for the attacker. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
EAN: 2147483647
Pages: 171
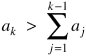

 1 mod
1 mod