Section 12.2. Recursive Definition

[Page 561]

12.2. Recursive Definition

One place you may have already seen recursion is in mathematics. A recursive definition consists of two parts: a recursive part in which the nth value is defined in terms of the (n-1)st value, and a nonrecursive, boundary, or base case, which defines a limiting condition.

12.2.1. Factorial: N!

For example, consider the problem of calculating the factorial of nthat is, n! for n 0. As you may recall,

n! = n * (n-1) * (n-2) * ... * 1, for n > 0

In addition, 0! is defined as 1. Let's now look at some examples for different values of n:

4! = 4 * 3 * 2 * 1 = 24 3! = 3 * 2 * 1 = 6 2! = 2 * 1 = 2 1! = 1 0! = 1

As these examples suggest, n! can always be calculated in terms of (n-1)! This relationship might be clearer if we rewrite the previous calculations as follows:

4! = 4 * 3 * 2 * 1 = 4 * 3! = 24 3! = 3 * 2 * 1     = 3 * 2! = 6 2! = 2 * 1         = 2 * 1! = 2 1!                 = 1 * 0! = 1 0!                 = 1

The only case in which we can't calculate n! in terms of (n-1)! is when n is 0. Otherwise, in each case we see that

n! = n * (n-1)!

This leads to the following recursive definition:

n! = 1          if n = 0    // Boundary (or base) case n! = n * (n-1)! if n > 0    // Recursive case

Note that if we had omitted the base case, the recursion would have continued to (-1)! and (-2)! and so on.

Debugging Tip: Bounding the Repetition

An infinite repetition will result if a recursive definition is not properly bounded.

[Page 562]

The recursive case uses divide and conquer to break the problem into a smaller problem, but the smaller problem is just a smaller version of the original problem. This combination of self-similarity and divide and conquer is what characterizes recursion. The base case is used to stop or limit the recursion.

Effective Design: Recursive Definition

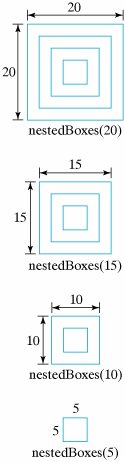
For recursive algorithms and definitions, the base case serves as the bound for the algorithm. The recursive case defines the nth case in terms of the (n - 1)st case.

12.2.2. Drawing a Nested Pattern

As another example, consider the problem of drawing the nested boxes pattern in Figure 12.2. The self-similarity occurs in the fact that for this pattern, the parts resemble the whole. The basic shape involved is a square, which is repeated over and over at an ever-smaller scale. A recursive definition for this pattern would be

Figure 12.2. The nested squares pattern.

Base case:      if side < 5 do nothing Recursive case: if side >= 5                     draw a square                     decrease the side and draw a smaller                                pattern inside the square

This definition uses the length of the square's side to help define the pattern. If the length of the side is greater than or equal to 5, draw a square with dimensions side x side. Then decrease the length of the side and draw a smaller version of the pattern inside that square. In this case, the side variable will decrease at each level of the drawing. When the length of the side becomes less than 5, the recursion stops. Thus, the length of the side serves as the limit or bound for this algorithm.

Note that the length of the side functions here like a parameter in a method definition: it provides essential information for the definition, just as a method parameter provides essential data to the method. Indeed, this is exactly the role that parameters play in recursive methods. They provide essential information that determines the method's behavior.

Figure 12.3 illustrates how we would apply the definition. Suppose the side starts out at 20 and decreases by 5 at each level of recursion. As you move from top to bottom across the four patterns, each pattern contains the one below it. A nestedBoxes(20) can be drawn by first drawing a 20x20 square and then drawing a nestedBoxes(15) pattern inside it. Similarly, a nestedBoxes(15) can be drawn by first drawing a 15 x 15 square and then drawing a nestedBoxes(10) pattern inside it. And so on.

[Page 563]

Figure 12.3. A trace of the nested boxes definition starting with a side of 20 and decreasing the side by 5 each time.

These examples illustrate the power of recursion as a problem-solving technique for situations that involve repetition. Like the iterative (looping) control structures we studied in Chapter 6, recursion is used to implement repetition within a bound. For recursive algorithms, the bound is defined by the base case, whereas for loops, the bound is defined by the loop's entry condition. In either case, repetition stops when the bound is reached.

Self-Study Exercises

Exercise 12.4Exercise 12.5

Exercise 12.3	You can calculate 2ⁿ by multiplying 2 by itself n times. For example, 2³ is 2 x 2 x 2. Note also that 2⁰ = 1. Given these facts, write a recursive definition for 2ⁿ, for n 0.
Generalize your solution to the preceding exercise by giving a recursive definition for xⁿ, where x and n are both integers 0.
Is the recursive definition given earlier for the nested boxes equivalent to the following recursive definition? Explain. Draw a square. // In every case If side > 5 draw a smaller nested boxes inside the square In this case, the base case (side <= 5) is implicit.
	[Page 564]
Exercise 12.6	Write a recursive definition for the recursive pattern shown in Figure 12.4. Figure 12.4. Write a recursive definition for this pattern.

Debugging Tip: Infinite Recursion

An unbounded or incorrectly bounded recursive algorithm will lead to infinite repetition. Care must be taken to get the boundary condition correct.