20.9 Data Structures for a Chess Program

I l @ ve RuBoard

A classic problem in artificial intelligence is the game of chess. We are going to design a data structure for a chess-playing program. In chess there are several moves you can make. Your opponent has many responses, to which you have many answers, and so on, back and forth for several levels of moves.

Our data structure is beginning to look like a tree. But this is not a binary tree, because we have more than two branches for each node (Figure 20-14).

Figure 20-14. Chess tree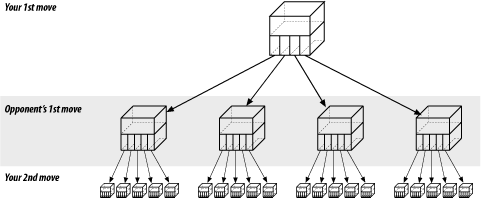

We are tempted to use the following data structure:

 class chess {      public:         class board_class board; // Current board position         class next_class {              class move_class move;        // Our next move             class chess *chess_ptr; // Pointer to the resulting position         } next[MAX_MOVES];  }; 

The problem is that the number of moves from any given position varies dramatically. For example, in the beginning you have lots of pieces running around. ^[2] Pieces such as rooks, queens, and bishops can move any number of squares in a straight line. When you reach the end game (in an evenly matched game), each side probably has only a few pawns and one major piece. The number of possible moves has been greatly reduced.

^[2] Trivia question: what are the 21 moves you can make in chess from the starting position? You can move each pawn up one (8 moves) or two (8 more), and the knights can move out to the left and right (4 more) (8+8+4=20). What's the 21st move?

We want to be as efficient as possible in our storage because a chess program stresses the limits of our machine. We can reduce storage requirements by changing the next-move array to a linked list. The resulting structure is:

 class next_class {      class move_class move;        // Our next move     class next_class *chess_ptr;  // Pointer to the resulting position };  struct chess {      class board_class board;     // Current board position     class next_class *list_ptr;  // List of moves we can make from here     class next_class this_move;  // The move we are making }; 

Graphically, this looks like Figure 20-15.

Figure 20-15. Revised chess structure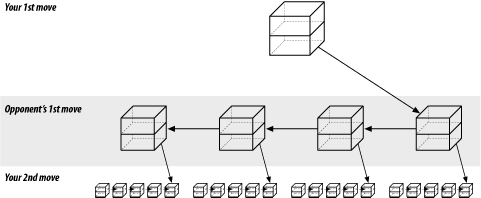

The new version adds a little complexity, but it saves a great deal of storage. That's because instead of having to allocate an array that contains all possible moves (whether used or not), we use a list to allocate only as many moves as we need to.

I l @ ve RuBoard