4.4 Public key cryptography

The idea of using one-way functions, which can only be inverted if a certain secret (a so-called trapdoor) is known, has led to the invention of public key cryptography or asymmetric cryptography [26]. ^[7] Today, public key cryptography is a battlefield for mathematicians and theoretical computer scientists. We are not going to delve into the mathematical details. Instead, we address public key cryptography from a practical point of view. From this point of view, a public key cryptosystem is simply a cryptosystem in which a user has a pair of mathematically related keys:

A public key that can be published without doing any harm to the system s overall security;
A private key that is assumed to never leave the possession of its owner.

For both the public and private keys, it must be computationally infeasible for an outsider to derive one from the other.

The use of a public key cryptosystem is overviewed in Figure 4.2. Again, A and B represent users, and the dark rectangles located in front of them represent the implementations of the cryptographic algorithms and protocols in use. A and B each has a key pair ( k _A , k _A ^-1 ) and ( k _B , k _B ^-1 ). The private keys k _A ^-1 and k _B ^-1 B must not be revealed to anyone , whereas the public keys k _A and k _B must be publicly available in certified form. This basically means that they are digitally signed by a certification authority as further addressed below.

If A wants to securely transfer a plaintext message P to B, she does the following things:

She gets the public key of B (i.e., k _B ) from an authentic source;
She encrypts P with k _B ;
She sends the resulting ciphertext C = E _KB ( P) to B. (The term C = E _KB ( P) is abbreviated with E _B ( P) in Figure 4.2).

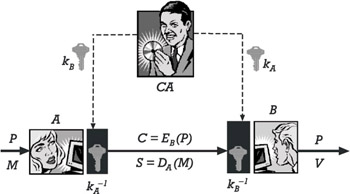
Figure 4.2: The use of a public key cryptosystem.

On the other side, B uses his private key k _B ^-1 B to successfully decrypt P = D _kB ^-1 (C) = D _kB ^-1 (E _kB (P)) .

A public key cryptosystem can be used not only to protect the confidentiality of a message, but also to protect its authenticity and integrity. If A wants to protect the authenticity and integrity of a message M , she creates a digital signature S = D _kA (M) (the term D _kA (M) is abbreviated with D _A (P) in Figure 4.2) for M and send it together with the message to B. Using the public key of A (i.e., k _A ), B can now verify the digital signature. Consequently, the value V in Figure 4.2 represents a boolean value (i.e., either the digital signature is correctly verified or it is not).

Digital signatures provide an electronic analog of handwritten signatures for electronic documents, and ”similar to handwritten signatures ”digital signatures must not be forgeable, recipients must be able to verify them, and the signers must not be able to repudiate them later. However, a major difference between a handwritten signature and a digital signature is that the digital signature cannot be constant, but must be a function of the document on which it appears. If this were not the case, a digital signature, because of its electronic nature, could be copied and attached to arbitrary documents.

Arbitrated digital signature schemes are based on secret key cryptography. In such a scheme, a trusted third party ( TTP ) validates the signature and forwards it on the signer s behalf . Obviously, this does not scale and requires a TTP that may become a bottleneck. Consequently, digital signature schemes should come along without TTPs taking an active role. They usually require the use of public key cryptography: Signed messages are sent directly from signers to recipients. In essence, a digital signature scheme consists of the following:

A key-generation algorithm that randomly selects a public key pair;
A signature algorithm that takes as input a message and a private key, and that generates as output a digital signature for the message;
A signature verification algorithm that takes as input a digital signature and a public key, and that generates as output a message and an information bit according to whether the signature is valid for the message. A comprehensive overview and discussion of public-key-based digital signature schemes are given in [27]. According to the OSI security architecture, a digital signature refers to data appended to, or a cryptographic transformation of, a data unit that allows a recipient of the data unit to prove the source and integrity of the data unit and protect against forgery (e.g., by the recipient). Consequently, there are two classes of digital signatures:

A digital signature giving message recovery refers to the situation in which a cryptographic transformation is applied to a data unit. In this case, the data is automatically recovered if the recipient verifies the signature.
A digital signature with appendix refers to the situation in which some cryptographically protected data is appended to the data unit. In fact, the data represents a digital signature and can be decoupled from the data unit that it signs.

The structure of a digital signature giving message recovery (a) and a digital signature with appendix (b) are illustrated in Figure 4.3. A dark rectangle represents an encrypted message part, whereas a white rectangle represents a message part that is not encrypted.

click to expand
Figure 4.3: The structure of a digital signature giving (a) message recovery and (b) a digital signature with appendix.

In the case of digital signatures with appendix, the bandwidth limitation of public key cryptography is unimportant because of the use of one-way hash functions as auxiliaries. A can use her private key k _A ^-1 to compute a digital signature S = D _A (M) or S = D _A (h(M)) for message M . In the second case, h refers to a cryptographic hash function that is applied to M before generating the digital signature. In summary, A does the following things when she computes and sends to B a digital signature with appendix for message M :

She uses a cryptographic hash function h to compute h(M) .
She encrypts h(M) with her private key k _A ^-1 . The result represents the digital signature that is appended to the message.
She transmits M and the digital signature to B.

On the other side, B does the following things to verify the signature:

He hashes the message M with the same cryptographic hash function h .
He decrypts the digital signature with A s public key (i.e., k _A ).
He verifies whether the two values match or not (the signature is verified only if the values match).

The use of public key cryptography considerably simplifies the problem of key distribution. Note that in Figure 4.2, instead of providing A and B with a unique session key that is protected in terms of confidentiality, integrity, and authenticity, the trusted third party, which is now called a certification authority (CA), has only to provide A and B with the public key of the communicating peer. This key is public in nature and need not be protected in terms of confidentiality. Nevertheless, the use of public key cryptography requires an authentication framework that binds public keys to user identities. As further addressed in Chapter 7, a public key certificate is a certified proof of such binding vouched for by a TTP acting as a CA. According to Webster s Dictionary , the term certificate refers to a document stating the truth. In the digital world we live in today, the term is mostly used to refer to a collection of information to which a digital signature has been affixed by some authority who is recognized and trusted by some community of certificate users. According to this definition, there exist various types of certificates that potentially may serve many purposes. In either case, a certificate is a form of credentials. Examples of credentials used in daily life are the driver s license, Social Security card, and birth certificate. Each of these credentials has some information on it identifying its owner and some authorization stating that someone else has confirmed the information.

A public key (or digital) certificate consists of three main elements:

1. A public key;

2. Certificate information that refers to the certificate owner s identity, such as his or her name ;

3. One or more digital signatures.

The aim of the digital signature(s) on the certificate is to state that the other certificate information has been attested to by some other person or entity.

A digital certificate can be one of a number of different formats, including, for example, PGP and ITU-T X.509. Again, this point is further addressed in Chapter 7. In the following sections, we overview some public key cryptosystems that are in widespread use today.

4.4.1 RSA

The most widely used public key cryptosystem is RSA, invented by Ronald L. Rivest, Adi Shamir, and Len M. Adleman at MIT in 1977 [28]. The RSA cryptosystem gets its security from the difficulty and intractability of the integer factorization problem. What this means is that it is fairly simple to multiply two large prime numbers , but difficult to compute the prime factors of a large number. One of the nice properties of RSA is that the same operation (i.e., exponentiation modulo a large number) can be used for both message encryption and decryption, as well as digital signature generation and verification. This is not the case for most other public key cryptosystems.

Mathematically spoken, the RSA public key cryptosystem requires two distinct large primes ( p and q ). Denote n = pq and ( (n) = (p-1)(q-1) , where ( refers to Euler s totient function . Each user chooses a large number d > 1 such that gcd(d, ( (n)) = 1 and computes the number e (1 < e < ( (n)) that satisfies the congruence ed ( 1 (mod ( (n)). The numbers n and e constitute the public key, whereas the remaining items p , q , ( (n) , and d form the private information. More commonly, d is referred to as the private key.

Against this background, message encryption and decryption work as follows :

To encrypt, one raises the plaintext block P to the power of e and reduces modulo n : C = P ^e (mod n );
To decrypt, one raises the ciphertext block C to the power of d and reduces modulo n : P = C ^d (mod n ).

Digital signature generation and verification uses the same algorithms with different keys (the private key is used to digitally sign a message, whereas the public key is used to verify the signature).

The RSA public key cryptosystem was protected by U.S. Patent No. 4,405,829 ˜ ˜Cryptographic Communications System and Method, issued and granted to MIT on September 20, 1983. The patent expired on September 20, 2000. Outside the U.S., the RSA public key cryptosystem has never been protected by a patent.

4.4.2 Diffie-Hellman

In 1977, Whitfield Diffie and Martin Hellman proposed a key agreement protocol that allows participants to agree on a key over an insecure public channel [26]. The protocol gets its security from the difficulty and intractability of the discrete logarithm problem in a finite group, such as the multiplicative group of a finite field. What this basically means is that, in general, the inverse operation of the exponentiation function is the logarithm function. There are efficient algorithms for computing logarithms in many groups; however, one does not know a polynomial-time algorithm for computing discrete logarithms in cyclic groups. For example, for a very large prime number p and two smaller numbers y and a , it is computationally intractable to find an x that satisfies the equation y = a ^x mod p . Mathematically speaking, the Diffie-Hellman key agreement protocol requires a finite cyclic group G of order G and generator a . To agree on a session key, A and B secretly choose elements x _A and x _B in G . These elements represent A and B s private keys. A and B then compute their public keys y _A = a ^xA and y _B = a ^xB , and exchange these public keys over an unsecured public channel. Finally, A and B compute K _AB = y ^xA _B = a ^xBxA and K _BA = y ^xB _A = a ^xAxB . Note that K _AB = K _BA , so this value can actually be used as a shared secret or session key to secure communications between A and B. Also note that an eavesdropper seeing either or both of the public keys cannot derive either private key nor the shared secret, because of the difficulty of the discrete logarithm problem.

The Diffie-Hellman key agreement protocol was protected by U.S. Patent No. 4,200,770, ˜ ˜Cryptographic Apparatus and Method, issued and granted to Stanford University on April 29, 1980. The patent expired in 1997. Similar to the RSA public key cryptosystem, the Diffie-Hellman key agreement protocol has never been protected by a patent outside the United States.

4.4.3 ElGamal

In the early 1980s, Taher ElGamal adapted the Diffie-Hellman key agreement protocol and came up with a public key cryptosystem that can be used for data encryption and digital signatures [29, 30]. Contrary to RSA, however, the ElGamal algorithms for data encryption and decryption are different from the the ElGamal algorithms for digital signature generation and verification. This is no serious drawback but is also not advantageous from an implementor s point of view.

Unlike many other public key cryptosystems, the ElGamal public key cryptosystem has not been patented in the U.S.

4.4.4 DSS

In the early 1990s, the U.S. NIST published the Digital Signature Standard (DSS) as a viable alternative to RSA signature schemes. The DSS refers to an optimized modification of the ElGamal cryptosystem that can be used only for digital signature generation and verification [31].

4.4.5 ECC

More recently, the use of elliptic curve cryptography (ECC) has attracted a lot of interest. ECC-based public key cryptosystems obtain their security from the difficulty and intractability of the elliptic curve discrete logarithm problem (that uses groups of points on elliptic curves). As illustrated in Table 4.2, a number of different types of cryptography have been defined over elliptic curves. The resulting ECC-based public key cryptosystems seem to be advantageous with regard to their security properties (meaning that smaller keys are required for a similar level of security). As such, they are particularly useful in situations where small keys are required (e.g., mobile and wireless applications).

Table 4.2: ECC-Based Public Key Cryptosystems
Acronym	Text
ECDH	Elliptic curve Diffie-Hellman key agreement
ECDSA	Elliptic curve digital signature algorithm
ECES	Elliptic curve encryption scheme
ECMQV	Elliptic curve MQV key agreement
ECNRA	Elliptic curve Nyberg-Rueppel signature scheme with appendix

Unlike RSA, the general category of ECC is not patented. Individual companies, however, have filed patents for specific efficiency or security algorithms that are related to ECC. Most importantly, the Certicom Corporation ^[8] holds several patents in this field.

^[7] http://csrc.nist.gov/encryption/aes

^[8] In spite of the fact that [26] is commonly used to refer to the invention of public key cryptography, similar ideas were pursued by Ralph C. Merkle.

Flylib.com

Category list

Similar pages

4.4 Public key cryptography