10.3 Roots and Logarithms

Team-Fly

In this section we shall develop functions for calculating the integer part of square roots and logarithms to base 2 of CLINT objects. To this end we first consider the latter of these two functions, since we will need it for the first of them: For a natural number a we are seeking a number e for which 2^e ≤ a < 2^e+1. The number e = ⌊log₂ a⌋ is the integer part of the logarithm of a to the base 2 and is easily obtained from the number of relevant bits of a, as determined from the following function ld_l(), reduced by 1. The function ld_l(), which is used in many other functions of the FLINT/C package, disregards leading zeros and counts only the relevant binary digits of a CLINT object.

Function:	number of relevant binary digits of a CLINT object
Syntax:	unsigned int ld_l (CLINT a_l);
Input:	a_l (operand)
Return:	number of relevant binary digits of a_l.

 unsigned int ld_l (CLINT n_l)   {     unsigned int l;     USHORT test;

Step 1: Determine the number of relevant digits to the base B.

   l = (unsigned int) DIGITS_L (n_l);   while (n_l[l] == 0 && l > 0)     {       --l;     }   if (l == 0)     {       return 0;     }

Step 2: Determine the number of relevant bits of the most-significant digit. The macro BASEDIV2 defines the value of a digit that has a 1 in the most-significant bit and otherwise contains 0 (that is, 2^{BITPERDGT−1}).

   test = n_l[l];   l <<= LDBITPERDGT;   while ((test & BASEDIV2) == 0)     {       test <<= 1;       --l;     }   return l; }

We then calculate the integer part of the square root of a natural number based on the classical method of Newton (also known as the Newton-Raphson method), which is used for determining the zeros of a function by successive approximation: We assume that a function f (x) is twice continuously differentiable on an interval [a, b], that the first derivative f′(x) is positive on [a, b], and that we have

Then if x_n Î [a, b] is an approximation for a number r with f(r) = 0, then x_n+1 := x_n − f (x_n) / f′ (x_n) is a better approximation of r. The sequence defined in this way converges to the zero r of f (cf. [Endl], Section 7.3).

If we set f (x) := x² − c with c > 0, then f(x) for x > 0 satisfies the above conditions for the convergence of the Newton method, and with

we obtain a sequence that converges to . Due to its favorable convergence behavior Newton's method is an efficient procedure for approximating square roots of rational numbers.

Since for our purposes we are interested in only the integer part r of , for which r² ≤ c < (r + 1)² holds, where c itself is assumed to be a natural number, we can limit ourselves to computing the integer parts of the elements of the sequence of approximations. We begin with a number x₁ > and continue until we obtain a value greater than or equal to its predecessor, at which point the predecessor is the desired value. It is naturally a good idea to begin with a number that is as close to as possible. For a CLINT object with value c and e := ⌊log₂c⌋ we have that ⌊2^(e+2)/2⌋ is always greater than , and furthermore, we can easily calculate it with the function ld_l(). The algorithm goes as follows.

Algorithm for determining the integer part r of the square root of a natural number c > 0

Set x ← ⌊2^(e+2)/2⌋ with e := ⌊log₂ c⌋.
Set y ← ⌊(x + c/x) /2⌋.
If y < x, set x ← y and go to step 2. Otherwise, output x and terminate the algorithm.

The proof of the correctness of this algorithm is not particularly difficult. The value of x decreases monotonically, and it is an integer and always positive, so that the algorithm certainly terminates. When this occurs, the condition y = ⌊(x + c/x) /2⌋ ≥ x holds, and we assume that x ≥ r + 1. From x ≤ r + 1 > it follows that x² > c, or c − x² < 0.

However,

in contradiction to the condition for terminating the process. Our assertion is therefore false, and we must have x = r. The following function uses integer division with remainder for the operation y ← ⌊(x + c/x) /2⌋ without putting the validity of the procedure at risk.

Function:	integer part of the square root of a CLINT object
Syntax:	void iroot_l(CLINT n_l, CLINT floor_l);
Input:	n_l (operand > 0)
Output:	floor_l (integer square root of n_l)

 void iroot_l (CLINT n_l, CLINT floor_l) {   CLINT x_l, y_l, r_l;   unsigned l;

With the function ld_l() and a shift operation l is set to the value ⌊(⌊log₂ (n_l)⌋ + 2) /2⌋, and y_l is set to 2^l with the help of setbit_l().

   l = (ld_l (n_l) + 1) >> 1;   SETZERO_L (y_l);   setbit_l (y_l, l);   do     {       cpy_l (x_l, y_l);

Steps 2 and 3. Newton approximation and checking for termination.

       div_l (n_l, x_l, y_l, r_l);       add_l (y_l, x_l, y_l);       shr_l (y_l);     }   while (LT_L (y_l, x_l));   cpy_l (floor_l, x_l); }

To determine whether a number n is the square of another number it suffices to square with sqr_l() the value output by iroot_l() and compare the result to n. If the values are unequal, then n is apparently not a square. One must, however, admit that this is not the most efficient method. There are criteria that in many cases can recognize such numbers that are not squares without the explicit calculation of root and square. Such an algorithm is given in [Cohe]. It uses four tables, q11, q63, q64, and q65, in which the quadratic residues modulo 11, 63, 64, and 65 are labeled with a "1" and the quadratic nonresidues with a "0":

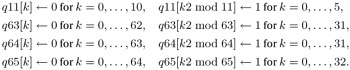
click to expand

From the representation of the residue class ring as the absolute smallest residue system (cf. page 68) one sees that we obtain all squares in this way.

Algorithm for identifying an integer n > 0 as a square. In this case the square root of n is output (from [Cohe], Algorithm 1.7.3)

Set t ← n mod 64. If q64[t] = 0, then n is not a square and we are done. Otherwise, set r ← n mod (11 · 63 · 65).
If q63[r mod 63] = 0, then n is not a square, and we are done.
If q65[r mod 65] = 0, then n is not a square, and we are done.
If q11[r mod 11] = 0, then n is not a square, and we are done.
Compute q ← ⌊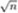⌋ using the function iroot_l(). If q² ≠ n, then n is not a square and we are done. Otherwise, n is a square, and the square root q is output.

This algorithm appears rather strange due to the particular constants that appear. But this can be explained: A square n has the property for any integer k that if it is a square in the integers, then it is a square modulo k. We have used the contrapositive: If n is not a square modulo k, then it is not a square in the integers. By applying steps 1 through 4 above we are checking whether n is a square modulo 64, 63, 65, or 11. There are 12 squares modulo 64, 16 squares modulo 63, 21 squares modulo 65, and 6 squares modulo 11, so that the probability that we are in the case that a number that is not a square has not been identified by these four steps is

It is only for these relatively rare cases that the test in step 5 is carried out. If this test is positive, then n is revealed to be a square, and the square root of n is determined. The order of the tests in steps 1 through 4 is determined by the individual probabilities. We have anticipated the following function in Section 6.5 to exclude squares as candidates for primitive roots modulo p.

Function:	determining whether a CLINT number n_l is a square
Syntax:	unsigned int issqr_l(CLINT n_l, CLINT r_l);
Input:	n_l (operand)
Output:	r_l (square root of n_l, or 0 if n_l is not a square)
Return:	1 if n_l is a square 0 otherwise

 static const UCHAR q11[11]=   {1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0}; static const UCHAR q63[63]=   {1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1,     0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0,     1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0}; static const UCHAR q64[64]=   {1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0,     0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0,     0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0}; static const UCHAR q65[65]=   {1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0,     0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0,     0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1}; unsigned int issqr_l (CLINT n_l, CLINT r_l) {   CLINT q_l;   USHORT r;   if (EQZ_L (n_l))     {       SETZERO_L (r_l);       return 1;     }   if (1 == q64[*LSDPTR_L (n_l) & 63])    /* q64[n_l mod 64]*/     {       r = umod_l (n_l, 45045);    /* n_l mod (11·63·65) */       if ((1 == q63[r % 63]) && (1 == q65[r % 65]) && (1 == q11[r % 11]))   /* Evaluation takes place from left to right; cf. [Harb], Section 7.7 */          {            iroot_l (n_l, r_l);            sqr_l (r_l, q_l);            if (equ_l (n_l, q_l))               {                 return 1;            }          }     }   SETZERO_L (r_l);   return 0; }

Team-Fly