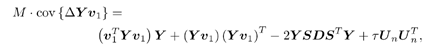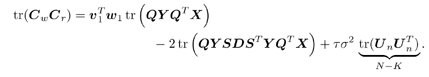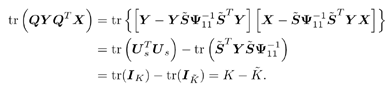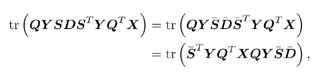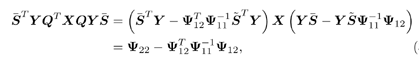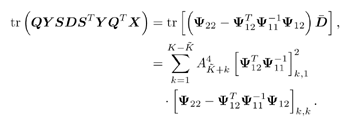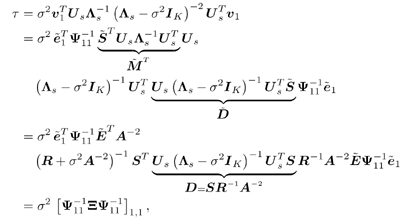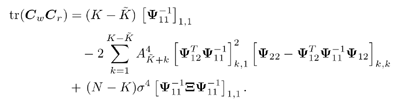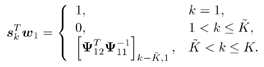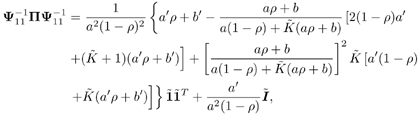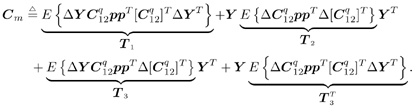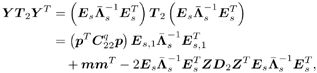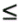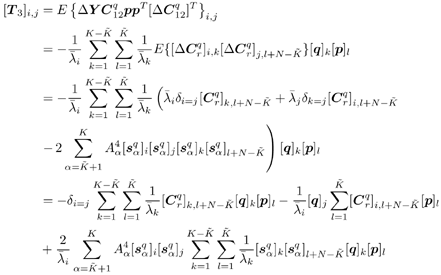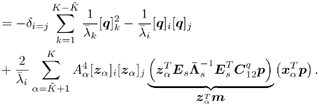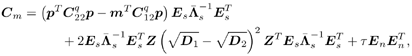3.6 Appendix
3.6.1 Proofs for Section 3.3.1Proof of Theorem 3.1 Denote Equation 3.231 The differential of the form II group -blind detector, Equation 3.232 is then given by Equation 3.233 It then follows from Lemma 2.6 that Equation 3.234 with Equation 3.235 Equation 3.236 Therefore, the asymptotic covariance of Equation 3.237 It is easily verified that QY u 1 = . Using this and the facts that w 1 = Y u 1 and QU n = U n , by substituting (3.234) into (3.237), we obtain (3.61). Proof of Corollary 3.1 In this appendix e k denotes the k th unit vector in Equation 3.238 Denote Equation 3.239 Equation 3.240 Equation 3.241 Equation 3.242 First we compute the term tr ( C w C r ). Using (3.61) and the facts that Equation 3.243 The term ( Equation 3.244 Using the fact that Equation 3.245 To compute the second term in (3.243), first note that Equation 3.246 where the first equality follows from the fact that QY Equation 3.247 where we used the fact that YXY = Y . In (3.246) Equation 3.248 Equation 3.249 Substituting (3.247) and (3.249) into (3.246) we obtain the second term in (3.243): Equation 3.250 Finally, we compute t in the last term in (3.243). By definition, Equation 3.251 where Equation 3.252 Equation 3.253 Equation 3.254 with Equation 3.255 Moreover, we have Equation 3.256 Next we compute w 1 2 . Since Equation 3.257 Equation 3.258 we have Equation 3.259 By (3.255) “(3.259) we obtain the corollary. SINR Calculation for Example 2Substituting (2.338) “(2.340) and A 2 = A 2 I K into (3.66) “(3.68), we have Equation 3.260 Equation 3.261 Equation 3.262 Equation 3.263 Equation 3.264 where Equation 3.265 Equation 3.266 Equation 3.267 Equation 3.268 Equation 3.269 Equation 3.270 Substituting (3.265) “(3.270) into (3.69) “(3.72), and letting Equation 3.271 Equation 3.272 Equation 3.273 Equation 3.274 Equation 3.275 we obtain (3.82). 3.6.2 Proofs for Section 3.3.2Proof of Theorem 3.2 We prove this theorem for the case of a linear group-blind hybrid detector (i.e., Denote e k as the k th unit vector in Equation 3.276 For any Equation 3.277 Equation 3.278 Equation 3.279 Denote Equation 3.280 Equation 3.281 where the dimension of Equation 3.282 Let the eigendecomposition of
Equation 3.283 Define another orthogonal transformation, Equation 3.284 For any Equation 3.285 Equation 3.286 Equation 3.287 Equation 3.288 Furthermore, after rotation, Equation 3.289 for some Equation 3.290 where E s consists of the first Equation 3.291 Let the corresponding eigendecomposition of Equation 3.292 Then the estimated detector in the same coordinate system is given by Note that in such a rotated coordinate system, estimation error occurs only in the first Equation 3.293 Equation 3.294 Hence Equation 3.295 By Lemma 2.6, Equation 3.296 We next compute the three terms T 1 , T 2 , and T 3 in (3.296). We first compute T 1 . Denote z k and x k as the subvectors of Equation 3.297 with Equation 3.298 Equation 3.299 The term T 2 can be computed following a similar derivation as in the proof of Theorem 1 for the DMI blind detector. Specifically, we have, similar to (2.302), Equation 3.300 Writing (3.300) in matrix form, we have Equation 3.301 with Equation 3.302 Hence the second term in (3.296) is Equation 3.303 where we have used the fact that Finally, we calculate T 3 . Denote Equation 3.304 As before, we only have to consider [ T 3 ] i,j for i,j Equation 3.305 Writing this in matrix form, we have Equation 3.306 Equation 3.307 Hence the third term in (3.296) is given by Equation 3.308 Substituting (3.297), (3.303), and (3.308) into (3.296), we obtain Equation 3.309 where D 1 and D 2 are given, respectively, by (3.299) and (3.302), and t is given by (3.298). Theorem 3 is now easily obtained by transforming (3.309) back to the original coordinate system according to the following mappings: |
EAN: 2147483647
Pages: 91
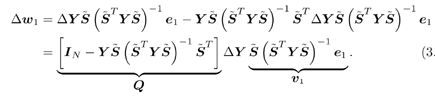
 range (
range (