Drawing with Transformations

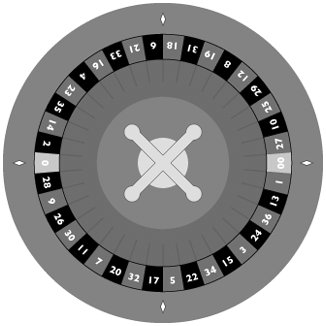
The key to using transformations effectively is working with them to simplify the drawing process. There are two jobs a Quartz 2D application needs to accomplish that transformations are particularly good at simplifying. The first job is when the application needs to construct the geometry that defines the graphics it wants to draw. The second job is positioning the individual graphic elements relative to one another. These are not the only two uses for transformations, but they are useful techniques to apply in your own code.

To demonstrate these techniques in a code setting, please refer to the graphic of a roulette wheel shown in Figure 5.11. The code sample that generated this figure is written in Python. You can view snippets from the code sample that show how the code uses transformations to simplify the construction of such a complex graphic in the following sections.

Figure 5.11. The Roulette Wheel

For this graphic, no transformations are applied to the geometric objects that make up the figure. Instead the methods of the CGContext that allow us to transform user space are used. As you read through the code sample, you may find it easier to follow the transformations if you keep the idea of user space as a flexible sheet in mind.

The first thing to note about the figure is that it has a circular symmetry. The first transformation that the code applies to the graphic is to move the origin of user space to the center of the graphics context. The code that initializes a number of code variables, creates the graphics context, and moves the user space origin to the center of that context is shown in Listing 5.1.

Listing 5.1. Initializing the Roulette Wheel Context

# initialize some of the variables that will help us draw the graphic # and create the context. fullCircle = 2 * math.pi; imageSize = 512; imageBounds = CGRectMake(0, 0, imageSize, imageSize); imageMidpoint. = CGPointMake(imageSize / 2, imageSize / 2); rgbSpace = CGColorSpaceCreateWithName(kCGColorSpaceGenericRGB); cgContext = CGBitmapContextCreateWithColor(imageSize, imageSize,                    rgbSpace, (0,0,0,0)) # exploit the circular symmetry of the graphic by # translating the coordinates # to the center of the context. cgContext.translateCTM(imageMidpoint.x, imageMidpoint.y) 

The roulette wheel code tries to create a graphic that the code can scale to any size. To do this, the code defines all of its geometry in a fixed size rectangle and uses a scale transformation to match that rectangle to the size of the context. For the roulette wheel, the code draws its graphics in a 256x256 rectangle. To scale the coordinate system so that the graphic will fill the context, the code uses the command

cgContext.scaleCTM(imageSize / 256.0, imageSize / 256.0) 

From here the code goes on to draw the green area in the center of the roulette wheel. To do this it simply creates circular paths and asks the computer to fill them in with green.

The next use of transformations in the code is to draw the radial lines in the green area. In this case the code simply draws lines and relies on a rotational transformation to position those lines in a circle. The code that accomplishes this is in Listing 5.2.

Listing 5.2. Drawing the Central Radial Lines

numSlots = 38; slotAngle = fullCircle / numSlots; cgContext.saveGState(); cgContext.setRGBStrokeColor(0, .38, 0, 1.0) cgContext.rotateCTM(-slotAngle / 2); for index in range(numSlots) :     cgContext.moveToPoint(innerGreenRadius + (2 * greenWidth / 5), 0);     cgContext.addLineToPoint(innerNumberRadius, 0);     cgContext.strokePath();     cgContext.rotateCTM(slotAngle); cgContext.restoreGState(); 

After calculating the angle that the computer uses to position the lines properly, the code saves the current graphics state. We save and restore the graphics state around the code that draws the lines to ensure that the CTM makes it back where it started after drawing the lines. The code rotates the context by half of the slot angle so that the first line matches up with the edge of the first slot. It next enters a simple loop that adds a line to the graphic and then rotates the context. Note that the line the computer draws lies along the x axis of the coordinate system. The lines end up in a circle because the orientation of that axis, relative to the device context, changes with each rotation.

The code uses a similar technique to draw the red and black backgrounds of the numbers. The code knows how to create the semi-circular wedges that make up these backgrounds. It simply uses a rotational transformation to repeat that graphic at fixed intervals around the circle. In this case the code is complicated a bit by the need to change the color of the shape depending on its position. Because the transformations involved are the same as those demonstrated in Listing 5.2, that code is not repeated here.

Drawing the numbers on the wheel uses this same rotational trick again, but it adds a slight twist. In the code sample of Chapter 3, was a routine that centers a particular text string around the origin. To get the numbers centered in their carefully constructed backgrounds, you not only use a rotation to orient the axes in the proper direction, but you combine that with a translation that moves the coordinate system away from the center of the figure and out to the band of alternating backgrounds. The code that draws the numbers can be found in Listing 5.3.

Listing 5.3. Combining Rotations and Translations to Draw the Numbers

# Draw the numbers fontSize = 8; textRadius = innerNumberRadius + (outerNumberRadius - innerNumberRadius) / 2 + (fontSize / 2); cgContext.selectFont("GillSans-Bold", fontSize, kCGEncodingMacRoman) cgContext.setRGBFillColor(1.0, 1.0, 1.0, 1.0); cgContext.saveGState() # rotate the y axis to point to the right cgContext.rotateCTM(-math.pi / 2); for index in range(numSlots) :     angle = index * slotAngle     cgContext.saveGState()     cgContext.translateCTM(0, textRadius - fontSize / 2);     CenterTextInContextAtPoint(cgContext, 0, 0, numberSequence[index])     cgContext.restoreGState()     cgContext.rotateCTM(slotAngle); cgContext.restoreGState(); 

This section of the code begins with some simple calculations to find the radial distance at which the text should be drawn. The first number that the code draws is the "00" slot of the wheel. Because Quartz always draws text so that "up" on the text points in the direction of the positive y axis, the first transformation rotates the coordinate system so that positive y points to the right. The code then enters a loop that contains two transformations. The inner transform moves the origin from the center of the figure, up the y axis, to the radial distance for the text that we calculated earlier. This puts the origin on the eventual baseline for the text, in the proper position within the number's field. After calling the routine that draws the number, the code restores the graphics state, which undoes the translation but leaves the y axis oriented through the center of the particular field we are drawing. The second rotation in the loop turns the y axis so that it points to the next slot along the wheel.

The code sample finishes the drawing with some simple embellishments that don't require much in the way of transformations. The final touch is the addition of the four diamonds on the outside edge of the wheel. The code that draws the diamonds uses the same technique that we used to draw the numbers. The code defines a simple routine that understands how to draw the diamond-shaped path centered on the origin. To position the individual diamonds, the code combines a rotation and a translation to move the origin to the right location and then draw the diamond.

Hopefully this code sample has given you some ideas about how you can use transformations to simplify the drawing process. This code sample understands how to draw a few basic shapes, lines, semi-circular wedges, and some basic text. It uses transformations to both help define these shapes, and position them relative to one another. Learning to apply transformations in the proper order requires a bit of practice and a healthy dose of creativity. Once you have the knack of how it is done, however, transformations can greatly simplify the drawing process.