12.4 Forward risk-neutral measure

The framework within which the HJM model is derived, in fact the framework within which the above analysis is performed, is the risk-neutral framework. This is characterised by a risk-neutral probability measure under which all discounted asset prices are martingales. Other risk-neutral probability measures may be defined in a similar way, allowing various asset/option pricing problems to be solved . Changing between probability measures is associated with numeraire changes. This allows the numeraire to be chosen in such as way as to expedite the option valuation procedure.

Consider a non-dividend-paying security X ( t ), which is a martingale under the risk-neutral probability measure . There exists a probability measure Q ^X such that the price of any asset relative to X is a Q ^X -martingale. The probability measure Q ^X is defined by the Radon-Nikodym derivative with respect to as [ 22 , Theorem 1]:

since the money market account B ( t ), is the numeraire asset associated with probability measure .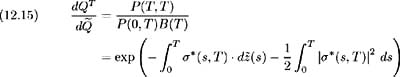

Calculating the time t price of an asset generating a cash flow at the future time T lends itself to a T -maturity discount bond as numeraire. Let Q ^T denote the probability measure associated with P ( t, T )( T -maturity discount bond) as numeraire. Making use of (12.14), we define this probability measure as:

Now since the relative price of a T -maturity discount bond is a martingale with respect to the risk-neutral measure and P (0, T ) is known at time t , we define:

By the Radon-Nikodym derivative (12.15), we have for any asset S ( ·):

and for conditional expectations we make use of Bayes' Rule to yield [ 49 ]:

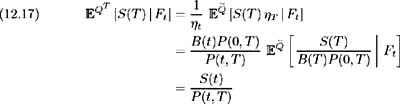
since the relative asset price is a martingale under probability measure and P (0, T ) is known at time t . Since the time t forward price for time T of asset S may be written as [ 41 ]:

we observe that the forward price process F _{S _T} ( t, T ), t ˆˆ [0, T ], follows a martingale ^[8] under the measure Q ^T . Hence this measure is referred to as the forward martingale measure or forward neutral probability measure.

We use Girsanov's Theorem (for example see [ 41 , Theorem B.2.1.]) to define the new Brownian motion under the forward martingale measure as:

^[8] Since

we may write

and hence F _{S _T} ( t, T ), t ˆˆ [0, T ] follows a martingale.