10.2 Binomial lattice specification
10.2 Binomial lattice specification
HL make use of a discrete time framework within which the stochastic process describing the evolution of the discount function is represented by a binomial lattice. At time n , P ( n ) i ( ·) represents the discount function after i upstate moves and ( n ˆ’ i ) downstate moves. During the ( n + 1) th period, that is from time n to time ( n + 1), the discount function may again be subject to one of two moves, an upstate move or a downstate move. Therefore, given the time n discount function P ( n ) i ( ·), two possible discount functions may occur at time ( n + 1), P i +1 ( n +1) ( ·) or P i ( n +1) ( ·) (see Figure 10.1). Within such a framework we have:
-
At each time n , there are ( n + 1) possible states, denoted by i , i = 0, , n .
-
The discount function in each state is independent of the path followed to get there. It is de ned by the number of upstate and downstate moves only.
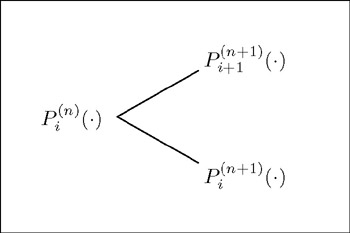
Figure 10.1: Binomial tree showing possible discount bond prices after one time step.
The price of each discount bond follows a binomial process where the step size is time-dependent. This feature greatly increases the explanatory power of the binomial lattice approach. When modelling the term structure with a view to pricing interest rate contingent claims, we are concerned with the movement of interest rates of various maturities relative to each other - that is the relative movement of different maturity discount bonds . For this reason the binomial lattice is used to model the entire term structure instead of just a specific bond. The time-dependent step size ensures the convergence, at maturity, of the bond price to unity.
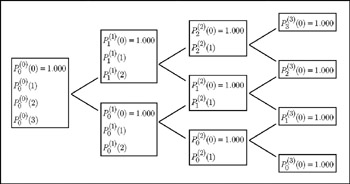
Figure 10.2: Binomial tree is used to model the whole term structure, not only the short-term interest rate.
The binomial lattice approach imparts the following characteristics on the stochastic process of the bond price:
-
Bond price uncertainty is small near bond maturity and in the immediate future.
-
Bond price uncertainty increases with distance from these two points.
These characteristics are a result of two factors:
-
For longer time horizons, the number of variations and hence uncertainty associated with the term structure increases.
-
As the time horizon approaches bond maturity, price uncertainty decreases since the bond price must converge to unity at maturity.
For a given bond, as the time horizon increases, the term structure uncertainty increases resulting in greater price variance. This is accompanied by the bond approaching maturity. At some future time horizon, the pull-to-par effect dominates, resulting in a decrease in bond price variability.
EAN: 2147483647
Pages: 132