8.4 Continuous time equivalent
8.4 Continuous time equivalent
The original specification of the BDT model is in a discrete time framework. There are several disadvantages associated with this type of formulation. The algorithmic manner in which one must view the model makes it difficult to identify the embedded assumptions and their implications, affecting , for example, the characteristics of the mean reversion. While the lognormality of the short- term interest rate is a positive feature since it precludes negative interest rates, it does make analytical analysis cumbersome [ 45 ]. We examine the continuous time equivalent of the BDT model [4] . Consider a process for the short-term interest rate r ( ·), as follows [5] :
where
| u ( t ) | - | time t median of the short-term interest rate distribution, |
| ƒ ( t ) | - | short-term interest rate volatility at time t , |
| z ( t ) | - | standard Brownian motion. |
To examine the nature of the stochastic process driving the short-term interest rate as modelled by BDT, we must examine the evolution of ln r ( t )where
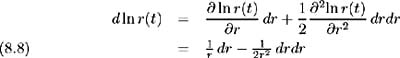
Since r ( t ) = r ( t, z ( t )) Ito's Lemma gives:
where
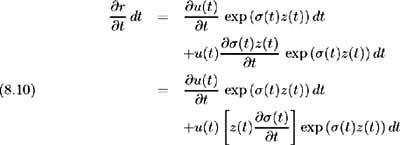
Substituting (8.7), (8.9)-(8.12) into (8.8) we have [6] :
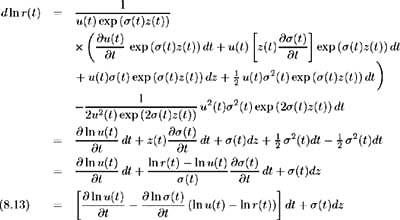
This is a mean reverting process that is explicitly dependent on the median of the distribution. This median is implicitly determined during the tree-fitting procedure.
If we allow the volatility to be constant, i.e. ƒ ( t ) ‰ ƒ ,then ![]() and there is no mean reversion. The logarithm of the short-term interest rate follows a simple diffusion with a drift that follows the logarithm of the median of the distribution. That is, the process simplifies to:
and there is no mean reversion. The logarithm of the short-term interest rate follows a simple diffusion with a drift that follows the logarithm of the median of the distribution. That is, the process simplifies to:
For a volatility that decays with time, i.e. ![]() the reversion speed becomes positive and the logarithm of the short-term interest rate ln r ( t ) reverts to the logarithm of the median ln u ( t ).
the reversion speed becomes positive and the logarithm of the short-term interest rate ln r ( t ) reverts to the logarithm of the median ln u ( t ).
This assumption of a decaying short-term interest rate volatility is necessary to ensure that the unconditional variance of the short-term interest rate ƒ 2 ( t ) t , does not increase without bound as t increases and the mean-reverting nature of the short-term interest rate process is maintained .
The reversion speed determines the volatility of rates for various maturities. In this model the reversion speed is a unique function of the short-term interest rate volatility ƒ ( t ), and hence we conclude that the entire term structure of volatilities is fully determined by the future short-term interest rate volatilities. This is unique to the BDT model, since other models, e.g. the Hull-White model [ 28 ], specify the reversion speed as an independent parameter. This artificial link created between the future short-term interest rate volatilities and the term structure of volatilities may be seen as one of the shortcomings of this model.
[4] Rebonato [ 45 ] details an analysis of binomial pricing within a lattice, which leads to the derivation of the continuous equivalent of the BDT model.
[5] In the BDT model, a lognormal distribution of the short-term interest rate is assumed. This implies that ln r ( t ) is normally distributed. At each time step t in a binomial lattice, we have t + 1 possible states of the world and hence t + 1 possible values of the one period rate. Consider time t = 1: we have two possible states of the world and interest rates denoted r (1, 1) and r (1, ˆ’ 1). The mean short-term interest rate at this time, ln r m (1) may be calculated as:
Knowing the time t = 0 percentage volatility of the short-term interest rate, i.e. ƒ (0), the standard deviation of the time t = 1 short-term interest rates is represented as:
and hence, we find each of the two possible rates as an offset from the median rate of interest, r m (1):
and
Note that the mean of the distribution of the logarithm of the short-term interest rate corresponds to the median of the lognormal distribution of the short-term interest rate. ln r ( t ) is normally distributed with mean ln r m (1) and r ( t ) is lognormally distributed with median r m (1).
[6] From (8.7) we have:
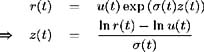
EAN: 2147483647
Pages: 132