7.2 Extension of the Vasicek model
7.2 Extension of the Vasicek model
HW propose an extension to the Vasicek model of the form:
This is (7.2) with ² = 0. Assuming that the market price of interest rate risk has the functional form » ( t ), and is bounded on any time interval (0, ), we may apply Ito's Lemma to derive the general partial differential equation that must be satisfied by any interest rate contingent claim, g :
The market price of risk represents the excess return required above the risk-free rate. This relationship is denoted by:
and so
where ( t ) = a ( t ) b + ( t ) ˆ’ » ( t ) ƒ ( t ). Assume that the price of the contingent claim g , has the form:
with boundary condition g ( r, T, T ) = 1. Now:
Substituting into (7.5):
Therefore to solve (7.7) we must solve the system of simultaneous equations:
For ( t ), ƒ ( t ) and a ( t ) constant, (7.8a) and (7.8b) are solved to yield the Vasicek model where the bond price has the form assumed in (7.6) with [1] :
For the extended, time-dependent model, ƒ ( t ) should be chosen to reflect the current and future volatilities of the short- term interest rate. A (0, T ) and B (0, T ) are coefficients associated with the current term structure and are hence functions of the current interest rate term structure, current term structure of spot/forward interest rate volatilities, and ƒ (0) (the current volatility of the short-term interest rate). Since the current term structure is observable, we are able to determine A (0, T ), B (0, T ) and ƒ ( t ). Therefore, we must determine A ( t, T ), B ( t, T ), a ( t ) and ( t ) in terms of A (0, T ), B (0, T ) and ƒ ( t ).
First, differentiate (7.8a) and (7.8b) with respect to T . From (7.8a) we have:
Also, from (7.8a):
Hence:
with A ( T, T )= 1 and A (0, T ) = ¾ where ¾ is some known value. Similarly differentiating (7.8b) with respect to T yields:
From (7.8b) we have:
Therefore:
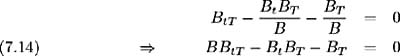
with B ( T, T ) = 0 and B (0, T ) = · where · is some known value. HW [ 28 ] solve (7.12) and (7.14) to yield:

where ‚ ( t, T ) = log A ( t, T )
We have solved for A ( t, T ) and B ( t, T ) in terms of the initial term structure.
Now solve for a ( t ) and ( t ). Differentiating (7.15) yields:
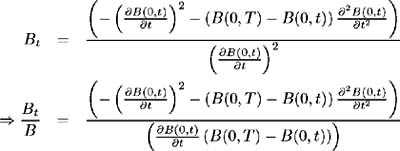
and so from (7.13) we solve for a ( t )as:
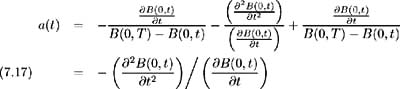
Differentiating (7.16) yields:
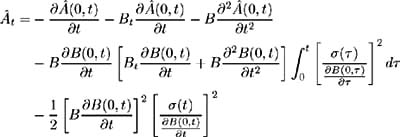
Since ‚ ( t, T ) = log A ( t, T ) we have:
Hence
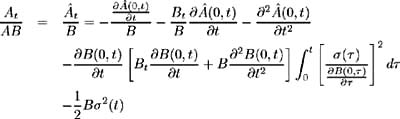
Therefore substituting into (7.11) we solve for ( t ) in terms of the initial term structure:
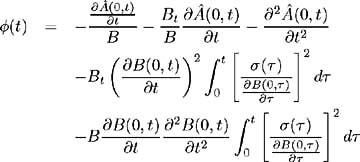
Also, from (7.8b) and (7.17) we have
and ![]()
Hence

and we have specified all the required model parameters in terms of the initial yield curve.
[1] These are the same formulae as calculated for the Vasicek model in Chapter 1 equations (1.25) and (1.26) with the following notational substitutions:
EAN: 2147483647
Pages: 132
- Integration Strategies and Tactics for Information Technology Governance
- Assessing Business-IT Alignment Maturity
- Measuring and Managing E-Business Initiatives Through the Balanced Scorecard
- A View on Knowledge Management: Utilizing a Balanced Scorecard Methodology for Analyzing Knowledge Metrics
- Measuring ROI in E-Commerce Applications: Analysis to Action