2.8 Bond pricing formula
2.8 Bond pricing formula
Allowing the bond price to take the form:
we have [18] :
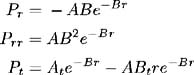
and so the bond price equation (2.18) reduces to:
Since the left-hand side is a function of the short- term interest rate r ( t ), while the right-hand side is independent of the short-term interest rate, the following two equations must be satisfied:
To solve for A ( t, T ) and B ( t, T ) first consider (2.29). This is a Ricatti equation [19] with solution B ( t, T ) = v ( t, T )/ u ( t, T )where v ( t, T ) and u ( t, T )are solutions to the following system of equations [20] :
Set = T ˆ’ t where T is the bond maturity date; then ![]() and the above system of equations may be written as:
and the above system of equations may be written as:
From (2.30) we have:
substituting into (2.31) gives:
Expressing this in terms of D -operators results in a simple quadratic equation:
The roots of this quadratic equation are ( ³ + » ˆ’ )/2 and ( ˆ’³ + » ˆ’ )/2 where ![]() and hence the solution may be written as:
and hence the solution may be written as:
where k 1 and k 2 are constants. Since B ( T,T ) = 0 = v (0)/ u (0), v (0) = 0 and hence k 1 = ˆ’ k 2 . Setting k 1 = 1 and k 2 = ˆ’ 1, v ( ) becomes:
Substituting (2.34) and
into (2.32) gives:
Since = T ˆ’ t , the solution of the Riccati equation is obtained from (2.34) and (2.35) as:

Now consider equation (2.28) with fixed bond maturity T , so the bond price is a function of t only. Hence:
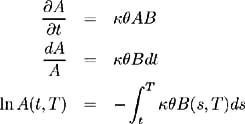
where and are constants. Substituting B ( t, T ) from (2.36) into (2.37):
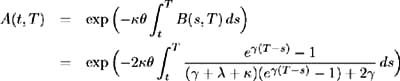
Let y = e ³ ( T ˆ’ s ) then ![]() and
and ![]() . Making this substitution and noting that ( ³ ˆ’ » ˆ’ )( ³ + » + ) = ³ 2 ˆ’ ( + » ) 2 = 2 ƒ 2 , the integral in the above equation becomes:
. Making this substitution and noting that ( ³ ˆ’ » ˆ’ )( ³ + » + ) = ³ 2 ˆ’ ( + » ) 2 = 2 ƒ 2 , the integral in the above equation becomes:
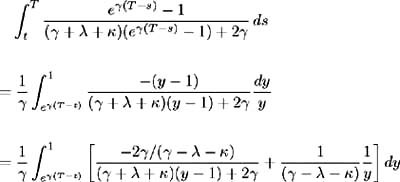

and hence the solution for A ( t, T )is:
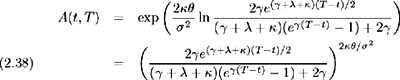
An analysis similar to that in the derivation of Vasicek's model in Chapter 1 can be applied to determine the bond price dynamics. Since the bond price is a function of the short-term interest rate, Ito's Lemma is used to give:
where
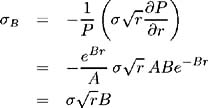
The existence of a factor risk premium q ( r, t ), implies:
Vasicek assumes a constant market price of risk, while CIR specify:
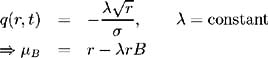
and hence under the CIR model the bond price process is specified by:
[18] Where the subscript indicates a partial derivative.
[19] The general form of the Ricatti equation is:
The solution of this equation can be written as w ( t ) = v ( t )/ u ( t ) where v ( t ) and u ( t )are solutions of the associated system of first order linear equations:
For more details on solving the Ricatti equation see [ 47 ].
[20] v and u are functions of t and T , but T is fixed, hence v ² ( t, T ) and ( t, T ) denote the derivative with respect to t .
EAN: 2147483647
Pages: 132