Cryptography: Theory and Practice:Identification Schemes | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

Basically, there are two things happening in the verification protocol. First, the signature s proves the validity of Alice’s certificate. Thus Bob verifies the signature of the TA on Alice’s certificate to convince himself that the certificate itself is authentic. This is essentially the same way that certificates were used in Chapter 8.

The second part of the protocol concerns the secret number a. The value a functions like a PIN in that it convinces Bob that the person carrying out the identification protocol is indeed Alice. But there is an important difference from a PIN: in the identification protocol, the value of a is not revealed. Instead Alice (or more accurately, Alice’s smart card) “proves” that she/it knows the value of a in step 5 of the protocol by computing the value y in response to the challenge r issued by Bob. Since the value of a is not revealed, this technique is called a proof of knowledge.

Figure 9.3 The Schnorr identification scheme

The following congruences demonstrate that Alice will be able to prove her identity to Bob:

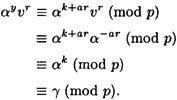
Thus Bob will accept Alice’s proof of identity (assuming he is honest), and the protocol is said to have the completeness property.

Here is a small (toy) example illustrating the challenge-and-response aspect of the protocol.

Example 9.2

Suppose p = 88667, q = 1031 and t = 10. The element α = 70322 has order q in 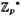. Suppose Alice’s secret exponent is a = 755; then

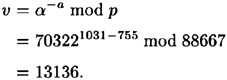
Now suppose Alice chooses k = 543. Then she computes

and sends γ to Bob. Suppose Bob issues the challenge r = 1000. Then Alice computes

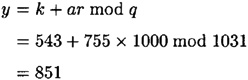
and sends y to Bob. Bob then verifies that

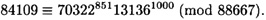
So Bob believes that he is communicating with Alice.

Next, let’s consider how someone might try to impersonate Alice. An imposter, Olga, might try to impersonate Alice by forging a certificate

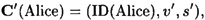
where v′ ≠ v. But s′ is supposed to be a signature of (ID (Alice), v′), and this is verified by Bob in step 3 of the protocol. If the signature scheme of the TA is secure, Olga will not be able to forge a signature s′ which will subsequently be verified by Bob.

Another approach would be for Olga to use Alice’s correct certificate, which is C(Alice) = (ID(Alice), v, s) (recall that certificates are not secret, and the information on a certificate is revealed each time the identification protocol is executed). But Olga will not be able to impersonate Alice unless she also knows the value of a. This is because of the “challenge” r in step 4. In step 5, Olga would have to compute y, but y is a function of a. The computation of a from v involves solving a discrete log problem, which we assume is intractible.

We can prove a more precise statement about the security of the protocol, as follows.

THEOREM 9.1

Suppose Olga knows a value γ for which she has probability ∈ ≥ 1/2^t-1 of successfully impersonating Alice in the verification protocol. Then Olga can compute a in polynomial time.

PROOF For a fraction ∈ of the 2^t possible challenges r, Olga can compute a value y which will be accepted in step 6 by Bob. Since ∈ ≥ 1/2 ^t-1, we have that 2^t ∈, and therefore Olga can compute values y₁, y₂, r₁ and r₂ such that

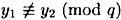
and

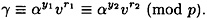
It follows that

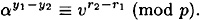
Since v = α^-a, we have that

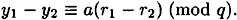
Now, 0 < |r₂ - r₁| < 2^t and q > 2^t is prime. Hence gcd(r₂ - r₁, q) = 1, and Olga can compute

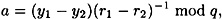
as desired.

The above theorem proves that anyone who has a non-negligible chance of successfully executing the identification protocol must know (or be able to compute in polynomial time) Alice’s secret exponent a. This property is often referred to as soundness.

We illustrate with an example.

Example 9.3

Suppose we have the same parameters as in Example 9.2: p = 88667, q = 1031, t = 10, α = 70322, α = 755 and v = 13136. Suppose Olga learns that

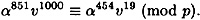
Then she can compute

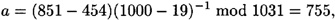
and thus discover Alice’s secret exponent.

We have proved that the protocol is sound and complete. But soundness and completeness are not sufficient to ensure that the protocol is “secure.” For example, if Alice simply revealed the value of her exponent a to prove her identity to Olga (say), the protocol would still be sound and complete. However, it would be completely insecure, since Olga could subsequently impersonate Alice.

This motivates the consideration of the secret information released to a verifier (or an observer) who takes part in the protocol (in this protocol, the secret information is the value of the exponent a). Our hope is that no information about a can be gained by Olga when Alice proves her identity, for then Olga would be able to masquerade as Alice.

In general, we could envision a situation whereby Alice proves her identity to Olga, say, on several different occasions. Perhaps Olga does not choose her challenges (i.e., the values of r) in a random way. After several executions of the protocol, Olga will try to determine the value of a so she can subsequently impersonate Alice. If Olga can determine no information about the value of a by taking part in a polynomial number of executions of the protocol and then performing a polynomial amount of computation, then we would be convinced that the protocol is secure.

It has not been proven that the Schnorr Scheme is secure. But in the next section, we present a modification of the Schnorr Scheme, due to Okamoto, that can be proved to be secure given a certain computational assumption.

Table of Contents