Cryptography: Theory and Practice:Classical Cryptography
 | Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210 Pub Date: 03/17/95 |
| Previous | Table of Contents | Next |
These definitions of addition and multiplication in 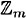 satisfy most of the familiar rules of arithmetic. We will list these properties now, without proof:
satisfy most of the familiar rules of arithmetic. We will list these properties now, without proof:
- 1. addition is closed, i.e., for any
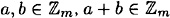
- 2. addition is commutative, i.e., for any
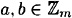 , a + b = b + a
, a + b = b + a - 3. addition is associative, i.e., for any
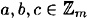 , (a + b) + c = a + (b + c)
, (a + b) + c = a + (b + c) - 4. 0 is an additive identity, i.e., for any
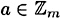 , a + 0 = 0 + a = a
, a + 0 = 0 + a = a - 5. the additive inverse of any
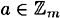 is m-a, i.e., a+(m-a) = (m-a)+a = 0 for any
is m-a, i.e., a+(m-a) = (m-a)+a = 0 for any 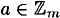
- 6. multiplication is closed, i.e., for any
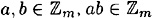
- 7. multiplication is commutative, i.e., for any
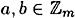 , ab = ba
, ab = ba 
Figure 1.2 Shift Cipher- 8. multiplication is associative, i.e., for any
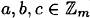 , (ab)c = a(bc)
, (ab)c = a(bc) - 9. 1 is a multiplicative identity, i.e., for any
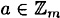 , a × 1 = 1 × a = a
, a × 1 = 1 × a = a - 10. multiplication distributes over addition, i.e., for any
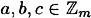 , (a+b)c = (ac) + (bc) and a(b + c) (ab) + (ac).
, (a+b)c = (ac) + (bc) and a(b + c) (ab) + (ac). - 2. addition is commutative, i.e., for any
Properties 1, 3-5 say that 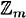 forms an algebraic structure called a group with respect to the addition operation. Since property 2 also holds, the group is said to be abelian.
forms an algebraic structure called a group with respect to the addition operation. Since property 2 also holds, the group is said to be abelian.
Properties 1-10 establish that 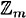 is, in fact, a ring. We will see many other examples of groups and rings in this book. Some familiar examples of rings include the integers,
is, in fact, a ring. We will see many other examples of groups and rings in this book. Some familiar examples of rings include the integers, 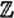 ; the real numbers,
; the real numbers, 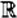 ; and the complex numbers,
; and the complex numbers, 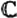 . However, these are all infinite rings, and our attention will be confined almost exclusively to finite rings.
. However, these are all infinite rings, and our attention will be confined almost exclusively to finite rings.
Since additive inverses exist in 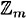 , we can also subtract elements in
, we can also subtract elements in 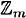 . We define a - b in
. We define a - b in 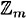 to be a + m - b mod m. Equivalently, we can compute the integer a - b and then reduce it modulo m.
to be a + m - b mod m. Equivalently, we can compute the integer a - b and then reduce it modulo m.
For example, to compute 11 - 18 in 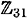 , we can evaluate 11 + 13 mod 31 = 24. Alternatively, we can first subtract 18 from 11, obtaining -7 and then compute -7 mod 31 = 24.
, we can evaluate 11 + 13 mod 31 = 24. Alternatively, we can first subtract 18 from 11, obtaining -7 and then compute -7 mod 31 = 24.
We present the Shift Cipher in Figure 1.2. It is defined over 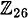 since there are 26 letters in the English alphabet, though it could be defined over
since there are 26 letters in the English alphabet, though it could be defined over 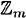 for any modulus m. It is easy to see that the Shift Cipher forms a cryptosystem as defined above, i.e., dK(eK(x)) = x for every
for any modulus m. It is easy to see that the Shift Cipher forms a cryptosystem as defined above, i.e., dK(eK(x)) = x for every 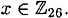
REMARK For the particular key K = 3, the cryptosystem is often called the Caesar Cipher, which was purportedly used by Julius Caesar.
We would use the Shift Cipher (with a modulus of 26) to encrypt ordinary English text by setting up a correspondence between alphabetic characters and residues modulo 26 as follows: A ↔ 0, B ↔ 1, . . . , Z ↔ 25. Since we will be using this correspondence in several examples, let’s record it for future use:
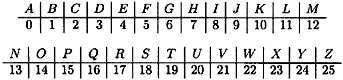
A small example will illustrate.
Example 1.1
Suppose the key for a Shift Cipher is K = 11, and the plaintext is
wewillmeetatmidnight.
We first convert the plaintext to a sequence of integers using the specified correspondence, obtaining the following:
| 22 | 4 | 22 | 8 | 11 | 11 | 12 | 4 | 4 | 19 |
| 0 | 19 | 12 | 8 | 3 | 13 | 8 | 6 | 7 | 19 |
Next, we add 11 to each value, reducing each sum modulo 26:
| 7 | 15 | 7 | 19 | 22 | 22 | 23 | 15 | 15 | 4 |
| 11 | 4 | 23 | 19 | 14 | 24 | 19 | 17 | 18 | 4 |
Finally, we convert the sequence of integers to alphabetic characters, obtaining the ciphertext:
HPHTWWXPPELEXTOYTRSE
To decrypt the ciphertext, Bob will first convert the ciphertext to a sequence of integers, then subtract 11 from each value (reducing modulo 26), and finally convert the sequence of integers to alphabetic characters.
REMARK In the above example we are using upper case letters for ciphertext and lower case letters for plaintext, in order to improve readability. We will do this elsewhere as well.
If a cryptosystem is to be of practical use, it should satisfy certain properties. We informally enumerate two of these properties now.
- 1. Each encryption function eK and each decryption function dK should be efficiently computable.
- 2. An opponent, upon seeing a ciphertext string y, should be unable to determine the key K that was used, or the plaintext string x.
The second property is defining, in a very vague way, the idea of “security.” The process of attempting to compute the key K, given a string of ciphertext y, is called cryptanalysis. (We will make these concepts more precise as we proceed.) Note that, if Oscar can determine K, then he can decrypt y just as Bob would, using dK. Hence, determining K is at least as difficult as determining the plaintext string x.
We observe that the Shift Cipher (modulo 26) is not secure, since it can be cryptanalyzed by the obvious method of exhaustive key search. Since there are only 26 possible keys, it is easy to try every possible decryption rule dK until a “meaningful” plaintext string is obtained. This is illustrated in the following example.
| Previous | Table of Contents | Next |
Copyright © CRC Press LLC
EAN: 2147483647
Pages: 133