Cryptography: Theory and Practice:Hash Functions | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

THEOREM 7.1

Suppose h : X → Z is a hash function where |X| and |Z| are finite and |X| ≥ 2|Z|. Suppose A is an inversion algorithm for h. Then there exists a probabilistic Las Vegas algorithm which finds a collision for h with probability at least 1/2.

PROOF Consider the algorithm B presented in Figure 7.2. Clearly B is a probabilistic algorithm of the Las Vegas type, since it either finds a collision or returns no answer. Thus our main task is to compute the probability of success. For any x ∈ X, define x ~ x₁ if h(x) = h(x₁). It is easy to see that ~ is an equivalence relation. Define

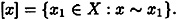
Each equivalence class [x] consists of the inverse image of an element of Z, so the number of equivalence classes is at most |Z|. Denote the set of equivalence classes by C.

Now, suppose x is the element of X chosen in step 1. For this x, there are |[x]| possible x₁’s that could be returned in step 3. |[x]| - 1 of these x₁’s are different from x and thus lead to success in step 4. (Note that the algorithm A does not know the representative of the equivalence class [x] that was chosen in step 1.) So, given a particular choice x ∈ X, the probability of success is (|[x]| - 1)/|[x]|.

Figure 7.2 Using an inversion algorithm A to find collisions for a hash function h

The probability of success of the algorithm B is computed by averaging over all possible choices for x:

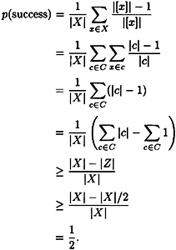
Hence we have constructed a Las Vegas algorithm with success probability at least 1/2.

Hence, it is sufficient that a hash function satisfy the strongly collision-free property, since it implies the other two properties. So in the remainder of this chapter we restrict our attention to strongly collision-free hash functions.

7.3 The Birthday Attack

In this section, we determine a necessary security condition for hash functions that depends only on the cardinality of the set Z (equivalently, on the size of the message digest). This necessary condition results from a simple method of finding collisions which is informally known as the birthday attack. This terminology arises from the so-called birthday paradox, which says that in a group of 23 random people, at least two will share a birthday with probability at least 1/2. (Of course this is not a paradox, but it is probably counter-intuitive). The reason for the terminology “birthday attack” will become clear as we progress.

As before, let us suppose that h : X → Z is a hash function, X and Z are finite, and |X| ≥ 2|Z|. Denote |X| = m and |Z| = n. It is not hard to see that there are at least n collisions — the question is how to find them. A very naive approach is to choose k random distinct elements x₁,...,x_k ∈ X, compute z_i = h(x_i), 1 ≤ i ≤ k, and then determine if a collision has taken place (by sorting the z_i’s, for example).

This process is analogous to throwing k balls randomly into n bins and then checking to see if some bin contains at least two balls. (The k balls correspond to the k random x_i’s, and the n bins correspond to the n possible elements of Z.)

We will compute a lower bound on the probability of finding a collision by this method. This lower bound will depend on k and n, but not on m. Since we are interested in a lower bound on the collision probability, we will make the assumption that 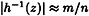for all z ∈ Z. (This is a reasonable assumption: if the inverse images are not approximately equal, then the probability of finding a collision will increase.)

Since the inverse images are all (roughly) the same size and the x_i’s are chosen at random, the resulting z_i’s can be thought of as random (not necessarily distinct) elements of Z. But it is a simple matter to compute the probability that k random elements z₁,...,z_k ∈ Z are distinct. Consider the z_i’s in the order z₁,...,z_k. The first choice z₁ is arbitrary; the probability that z₂ ≠ z₁ is 1 - 1/n; the probability that z₃ is distinct from z1 and z₂ is 1 - 2/n, etc.

Hence, we estimate the probability of no collisions to be

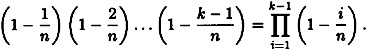
If x is a small real number, then 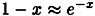. This estimate is derived by taking the first two terms of the series expansion

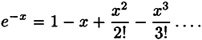
Then our estimated probability of no collisions is

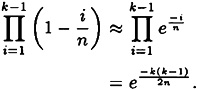
So we estimate the probability of at least one collision to be

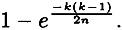
If we denote this probability by ∈, then we can solve for k as a function of n and ∈.

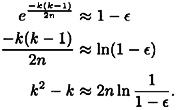
If we ignore the term -k, then we estimate

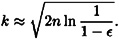
If we take ∈ = .5, then our estimate is

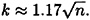
So this says that hashing just over 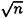random elements of X yields a collision with a probability of 50%. Note that a different choice of ∈ leads to a different constant factor, but k will still be proportional to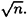

If X is the set of all human beings, Y is the set of 365 days in a non-leap year (i.e., excluding February 29), and h(x) denotes the birthday of person x, then we are dealing with the birthday paradox. Taking n = 365 in our estimate, we get 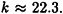Hence, as mentioned earlier, there will be at least one duplicated birthday among 23 random people with probability at least 1/2.

Table of Contents