Cryptography: Theory and Practice:Signature Schemes | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

Another complaint about the DSS was that signatures can be generated considerably faster than they can be verified. In contrast, if RSA is used as a signature scheme and the public verification exponent is very small (say 3, for example), then verification can be performed much more quickly than signing. This leads to a couple of considerations concerning the potential applications of the signature scheme:

1. A message will only be signed once. On the other hand, it might be necessary to verify the signature many times over a period of years. This suggests that a faster verification algorithm would be desirable.

Figure 6.4 Lamport Signature Scheme

2. What types of computers are likely to be doing the signing and verifying? Many potential applications involve smart cards, with limited processing power, communicating with a more powerful computer. So one might try to design a scheme so that fewer computations are likely to be done by a card. But one can imagine situations where a smart card would generate a signature, and other situations where a smart card would verify a signature, so it is difficult to give a definitive answer here.

The response of NIST to the question of signature generation/verification times is that it does not really matter which is faster, provided that both can be done sufficiently quickly.

6.4 One-time Signatures

In this section, we describe a conceptually simple way to construct a one-time signature scheme from any one-way function. The term “one-time” means that only one message can be signed. (The signature can be verified an arbitrary number of times, of course.) The description of the scheme, known as the Lamport Signature Scheme, is given in Figure 6.4.

Informally, this is how the system works. A message to be signed is a binary k-tuple. Each bit is signed individually: the value z_i,j corresponds to the ith bit of the message having the value j (j = 0, 1). Each z_i,j is the image of y_i,j under the one-way function f. The ith bit of the message is signed using the preimage y_i,j of the z_i,j corresponding to the ith bit of the message. The verification consists simply of checking that each element in the signature is the preimage of the appropriate public key element.

We illustrate the scheme by considering one possible implementation using the exponentiation function f(x) = α^x mod p, where α is a primitive element modulo p.

Example 6.4

7879 is prime and 3 is a primitive element in 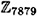. Define

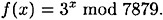
Suppose Bob wishes to sign a message of three bits, and he chooses the six (secret) random numbers

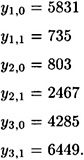
Then he computes the images of the y’s under the function f:

These z’s are published. Now, suppose Bob wants to sign the message

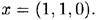
The signature for x is

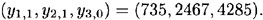
To verify this signature, it suffices to compute the following:

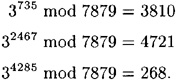
Hence, the signature is valid.

Oscar cannot forge a signature because he is unable to invert the one-way function f to obtain the secret y’s. However, the signature scheme can be used to sign only one message. For, given signatures for two different messages, it is (usually) an easy matter for Oscar to construct signatures for further messages (different from the first two).

For example, suppose the messages (0, 1, 1) and (1, 0, 1) are both signed using the same scheme. The message (0, 1, 1) would have as its signature the triple (y_1,0, y_2,1, y_3,1), and the message (1, 0, 1) would be signed with (y_1,1, y_2,0, y_3,1). Given these two signatures, Oscar can manufacture signatures for the messages (1, 1, 1) (namely, (y_1,1, y_2,1, y_3,1)) and (0, 0, 1) (namely, (y_1,0, y_2,0, y_3,1)).

Even though this scheme is quite elegant, it is not of great practical use due to the size of the signatures it produces. For example, if we use the modular exponentiation function, as in the example above, then a secure implementation would require that p be at least 512 bits in length. This means that each bit of the message is signed using 512 bits. Consequently, the signature is 512 times as long as the message!

We now look at a modification due to Bos and Chaum that allows the signatures to be made somewhat shorter, with no loss of security. In the Lamport Scheme, the reason that Oscar cannot forge a signature on a (second) message, given a signature on one message, is that the y’s corresponding to one message are never a subset of the y’s corresponding to another (distinct) message.

Suppose we have a set 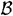of subsets of a set B such that 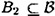only if B₁ = B₂, for all B₁, 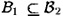. Then 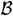is said to satisfy the Sperner property. Given a set B of even cardinality 2n, it is known that the maximum size of a set 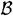of subsets of B having the Sperner property is 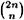. This can easily be obtained by taking all the n-subsets of B: clearly no n-subset is contained in another n-subset.

Now suppose we want to sign a k-bit message, as before, and we choose n large enough so that

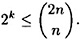
Let |B| = 2n and let 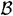denote the set of n-subsets of B. Let 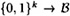be a publicly known injection. Then we can associate each possible message with an n-subset in 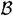. We will have 2n y’s and 2n z’s, and each message will be signed with n y’s. The complete description of the Bos-Chaum Scheme is given in Figure 6.5.

Table of Contents