Cryptography: Theory and Practice:The Data Encryption Standard | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

3.5 A Time-memory Trade-off

In this section, we describe an interesting time-memory tradeoff for a chosen plaintext attack. Recall that in a chosen plaintext attack, Oscar obtains a plaintext-ciphertext pair produced using the (unknown) key K. So Oscar has x and y, where y = e_K(x), and he wants to determine K.

A feature of this time-memory trade-off is that it does not depend on the “structure” of DES in any way. The only aspects of DES that are relevant to the attack are that plaintexts and ciphertexts have 64 bits, while keys have 56 bits.

Figure 3.6 Computation of X (i, j)

We have already discussed the idea of exhaustive search: given a plaintext-ciphertext pair, try all 2⁵⁶ possible keys. This requires no memory but, on average, 2⁵⁵ keys will be tried before the correct one is found. On the other hand, for a given plaintext x, Oscar could precompute y_K = e_K(x) for all 2⁵⁶ keys K, and construct a table of ordered pairs (y_K, K), sorted by their first coordinates. At a later time, when Oscar obtains the ciphertext y which is an encryption of plaintext x, he looks up the value y in the table, immediately obtaining the key K. Now the actual determination of the key requires only constant time, but we have a large memory requirement and a large precomputation time. (Note that this approach would yield no advantage in total computation time if only one key is to be found, since constructing the table takes at least as much time as an exhaustive search. The advantage occurs when several keys are to be found over a period of time, since the same table can be used in each case.)

The time-memory trade-off combines a smaller computation time than exhaustive search with a smaller memory requirement than table look-up. The algorithm can be described in terms of two parameters m and t, which are positive integers. The algorithm requires a reduction function R which reduces a bitstring of length 64 to one of length 56. (R might just discard eight of the 64 bits, for example.) Let x be a fixed plaintext string of length 64. Define the function 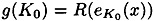for a bitstring K₀ of length 56. Note that g is a function that maps 56 bits to 56 bits.

In the pre-processing stage, Oscar chooses m random bitstrings of length 56, denoted X (i, 0), 1 ≤ i ≤ m. Oscar computes X(i, j) for 1 ≤ j ≤ t according to the recurrence relation X(i, j) = g (X(i, j - 1)), 1 ≤ i ≤ m, 1 ≤ j ≤ t, as indicated in Figure 3.6.

Then Oscar constructs a table of ordered pairs T = (X(i, t), X(i, 0)), sorted by their first coordinate (i.e., only the first and last columns of X are stored).

At a later time, Oscar obtains a ciphertext y which is an encryption of the chosen plaintext x (as before). He again wants to determine K. He is going to determine if K is in the first t columns of the array X, but he will do this by looking only at the table T.

Figure 3.7 DES time-memory trade-off

Suppose that K = X (i, t -j) for some j, 1 ≤ j ≤ t (i.e., suppose that K is in the first t columns of X). Then it is clear that g^j (K) = X (i, t), where g^j denotes the function obtained by iterating g, j times. Now, observe that

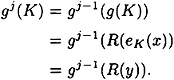
Suppose we compute y_j, 1 ≤ j ≤ t, from the recurrence relation

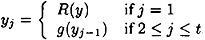
Then it follows that y_j = X(i, t) if K = X(i, t - j). However, note that y_j = X(i, t) is not sufficient to ensure that K = X(i, t - j). This is because the reduction function R is not an injection: The domain of R has cardinality 2⁶⁴ and the range of R has cardinality 2⁵⁶, so, on average, there are 2⁸ = 256 pre-images of any given bitstring of length 56. So we need to check whether y = e_{X(i,t - j)} (x), to see if X(i, t - j) is indeed the key. We did not store the value X(i, t - j), but we can easily re-compute it from X(i, 0) by iterating the g function t - j times.

Oscar proceeds according to the algorithm presented in Figure 3.7.

By analyzing the probability of success for the algorithm, it can be shown that if 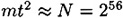, then the probability that K = X(i,t - j) for some i, j is about 0.8mt/N. The factor 0.8 accounts for the fact that the numbers X(i,t) may not all be distinct. It is suggested that one should take 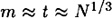and construct about N^1/3 tables, each using a different reduction function R. If this is done, the memory requirement is 112 × N^2/3 bits (since we need to store 2 × N^2/3 integers, each of which has 56 bits). The precomputation time is easily seen to be O(N).

The running time is a bit more dificult to analyze. First, note that step 3 can be implemented to run in (expected) constant time (using hash coding) or (worst-case) time O(log m) using a binary search. If step 3 is never satisfied (i.e., the search fails), then the running time is O(N^2/3). A more detailed analysis shows that even when the running time of steps 4 and 5 is taken into account, the expected running time increases by only a constant factor.

Table of Contents