Cryptography: Theory and Practice:Zero-knowledge Proofs | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

13.2 Perfect Zero-knowledge Proofs

Although interactive proof systems are of interest in their own right, the most interesting type of interactive proof is a zero-knowledge proof. This is one in which Peggy convinces Vic that x possesses some specified property, but at the end of the protocol, Vic still has no idea of how to prove (himself) that x has this property. This is a very tricky concept to define formally, and we present an example before attempting any definitions.

In Figure 13.4, we present a zero-knowledge interactive proof for Graph Isomorphism. A small example will illustrate the workings of the protocol.

Example 13.2

Suppose G₁ = (V, E₁) and G₂ = (V, E₂), where V = {1, 2, 3, 4}, E1 = {12, 13, 14, 34} and E2 = {12, 13, 23, 24}. One isomorphism from G₂ to G₁ is the permutation σ = (4 1 3 2).

Now suppose in some round of the protocol that Peggy chooses the permutation π = (2 4 1 3). Then H has edge set {12, 13, 23, 24} (see Figure 13.5).

If Vic’s challenge is i = 1, then Peggy gives Vic the permutation π and Vic checks that the image of G₁ under π is H. If Vic’s challenge is i = 2, then Peggy gives Vic the composition ρ = π 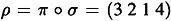σ = (3 2 1 4) and Vic checks that the image of G₂ under ρ is H.

Completeness and soundness of the protocol are easy to verify. It is easy to see that the probablity that Vic accepts is 1 if G₁ is isomorphic to G₂. On the other hand, if G₁ is not isomorphic to G₂, then the only way for Peggy to deceive Vic is for her to correctly guess the value i that Vic will choose in each round, and write a (random) isomorphic copy of G_i on the communication tape. Her probability of correctly guessing Vic’s n random challenges is 2^-n.

Figure 13.4 A perfect zero-knowledge interactive proof system for Graph Isomorphism

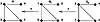
Figure 13.5 Peggy’s isomorphic graphs

All of Vic’s computations can be done in polynomial time (as a function of n, the number of vertices in G₁ and G₂). Although it is not necessary, notice that Peggy’s computations can also be done in polynomial time provided that she knows the existence of one permutation a such that the image of G₂ under σ is G₁.

Why would we refer to this proof system as a zero-knowledge proof? The reason is that, although Vic is convinced that G₁ is isomorphic to G₂, he does not gain any “knowledge” that would help him find a permutation σ that carries G₂ to G₁. All he sees in each round of the proof is a random isomorphic copy H of the graphs G₁ and G₂, together with a permutation that carries G₁ to H or G₂ to H (but not both!). But Vic can compute random isomorphic copies of these graphs by himself, without any help from Peggy. Since the graphs H are chosen independently and at random in each round of the proof, it seems unlikely that this will help Vic find an isomorphism from G₁ to G₂.

Let us look carefully at the information that Vic obtains by participating in the interactive proof system. We can represent Vic’s view of the interactive proof by means of a transcript that contains the following information:

1. the graphs G₁ and G₂

2. all the messages that are transmitted by both Peggy and Vic

3. the random numbers used by Vic to generate his challenges.

Hence, a transcript T for the above interactive proof of Graph Isomorphism would have the following form:

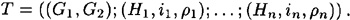
The essential point, which is the basis for the formal definition of zero-knowledge proof, is that Vic (or anyone else) can forge transcripts — without participating in the interactive proof — that “look like” real transcripts. This can be done provided that the input graphs G₁ and G₂ are isomorphic. Forging is accomplished by means of the algorithm presented in Figure 13.6. The forging algorithm is a polynomial-time probabilistic algorithm. In the vernacular of zero-knowledge proofs, a forging algorithm is often called a simulator.

Table of Contents