Cryptography: Theory and Practice:Secret Sharing Schemes | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

If Γ is an access structure, then B ∈ Γ is a minimal authorized subset if A ∉ Γ whenever 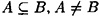. The set of minimal authorized subsets of Γ is denoted Γ₀ and is called the basis of Γ. Since Γ consists of all subsets of 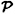that are supersets of a subset in the basis Γ₀, Γ is determined uniquely as a function of Γ₀. Expressed mathematically, we have

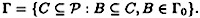
We say that Γ is the closure of Γ₀ and write

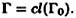
Example 11.2

Suppose and

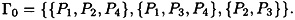
Then

Conversely, given this access structure Γ, it is easy to see that Γ₀ consists of the minimal subsets in Γ.

In the case of a (t, w)-threshold access structure, the basis consists of all subsets of (exactly) t participants.

11.3 The Monotone Circuit Construction

In this section, we will give a conceptually simple and elegant construction due to Benaloh and Leichter that shows that any (monotone) access structure can be realized by a perfect secret sharing scheme. The idea is to first build a monotone circuit that “recognizes” the access structure, and then to build the secret sharing scheme from the description of the circuit. We call this the monotone circuit construction.

Suppose we have a boolean circuit C, with w boolean inputs, x₁, . . . , x_w (corresponding to the w participants P₁, . . . , P_w), and one boolean output, y. The circuit consists of “or” gates and “and” gates; we do not allow any “not” gates. Such a circuit is called a monotone circuit. The reason for this nomenclature is that changing any input x_i from “0” (false) to “1” (true) can never result in the output y changing from “1” to “0.” The circuit is permitted to have arbitrary fan-in, but we require fan-out equal to 1 (that is, a gate can have arbitrarily many input wires, but only one output wire).

If we specify boolean values for the w inputs of such a monotone circuit, we can define

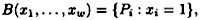
i.e., the subset of 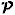corresponding to the true inputs. Suppose C is a monotone circuit, and define

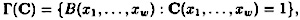
where C (x₁, . . . , x_w) denotes the output of C, given inputs x₁, . . . , x_w. Since the circuit C is monotone, it follows that Γ(C) is a monotone set of subsets of .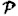

It is easy to see that there is a one-to-one correspondence between monotone circuits of this type and boolean formulae which contain the operators (“and”) and 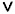(“or”), but do not contain any negations.

If Γ is a monotone set of subsets of , then it is easy to construct a monotone circuit C such that Γ(C) = Γ. One way to do this is as follows. Let Γ₀ be the basis of Γ. Then construct the disjunctive normal form boolean formula

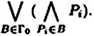
In Example 11.2, where

we would obtain the boolean formula

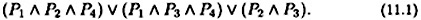
Each clause in the boolean formula corresponds to an “and” gate of the associated monotone circuit; the final disjunction corresponds to an “or” gate. The number of gates in the circuit is |Γ₀| + 1.

Suppose C is any monotone circuit that recognizes Γ (note that C need not be the circuit described above.) We describe an algorithm which enables D, the dealer, to construct a perfect secret sharing scheme that realizes Γ. This scheme will use as a building block the (t, t)-schemes constructed in Figure 11.2. Hence, we take the key set to be 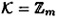for some integer m.

The algorithm proceeds by assigning a value 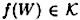to every wire W in the circuit C. Initially, the output wire W_out of the circuit is assigned the value K, the key. The algorithm iterates a number of times, until every wire has a value assigned to it. Finally, each participant P_i is given the list of values f(W) such that W is an input wire of the circuit which receives input x_i.

A description of the construction is given in Figure 11.3. Note that, whenever a gate G is an “and” gate having (say) t input wires, we share the “key” f(W_G) among the input wires using a (t, t)-threshold scheme.

Let’s carry out this procedure for the access structure of Example 11.2, using the circuit corresponding to the boolean formula (11.1).

Table of Contents