Cryptography: Theory and Practice:Authentication Codes | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

Example 10.2

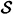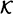Consider the authentication matrix of Figure 10.4. Suppose the probability distributions on and are

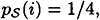
1 ≤ i ≤ 4; and

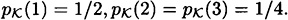
The values payoff (s, a) are as follows:

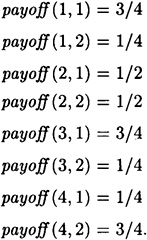
Hence, Pd₀ = 3/4. Oscar’s optimal impersonation strategy is to place any of the messages (1, 1), (3, 1) or (4, 2) into the channel.

Now we turn to the computation of Pd₁. First, we present the various values payoff (s′, a′; s, a) in the form of a matrix. The entry in row (s, a) and column (s′, a′) is the value payoff (s′, a′; s, a).

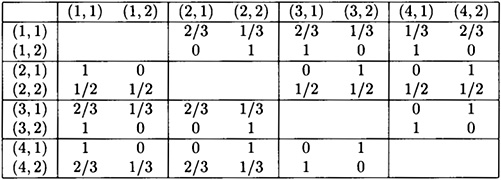
Thus we have p_1,1 = 2/3, p_2,2 = 1/2, and p_s,a = 1 for all other s, a. It is then a simple matter to evaluate Pd₁ = 7/8. An optimal substitution strategy for Oscar is as follows:

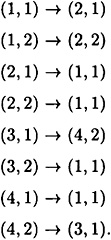
This strategy indeed yields Pd₁ = 7/8.

The computation of Pd₁ in Example 10.2 is straightforward but lengthy. We can in fact simplify the computation of Pd₁ by observing that we divide by the quantity payoff (s, a) in the computation of p_s_,a, and then later multiply by payoff (s, a) in the computation of Pd₁. Of course, these two operations cancel each other out. Suppose we define

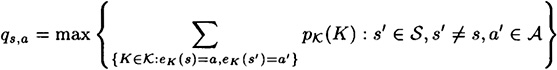
for all s, a. Then we have the following more concise formula for Pd₁:

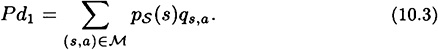
10.3 Combinatorial Bounds

We have seen that the security of an authentication code is measured by the deception probabilities. Hence, we want to construct codes so that these probabilities are as small as possible. But other considerations are also important. Let’s consider the various objectives that we might strive for in an authentication code:

1. The deception probabilities Pd₀ and Pd₁ must be small enough to obtain the desired level of security.

2. The number of source states must be large enough so that we can communicate the desired information by appending an authentication tag to one source state.

3. The size of the key space should be minimized, since the value of the key must be communicated over a secure channel. (Note that the key must be changed every time a message is communicated, as is done with the One-time Pad.)

In this section, we determine lower bounds on the deception probabilities, which will be computed in terms of other parameters of the code. Recall that we have defined an authentication code to consist of a four-tuple 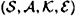. Throughout this section, we will denote .

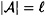Suppose we fix a source state 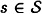. Then we can compute:

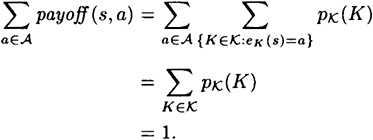
Hence, for every 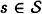, there exists an authentication tag a(s) such that

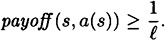
The following theorem follows easily.

THEOREM 10.1

Suppose 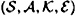is an authentication code. Then 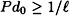, where 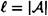. Further, 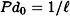if and only if

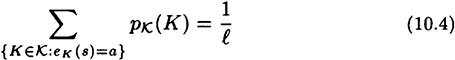
for every .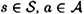

Now, we turn our attention to substitution. Suppose we fix s, a and s′, where s′ ≠ s. Then we have the following:

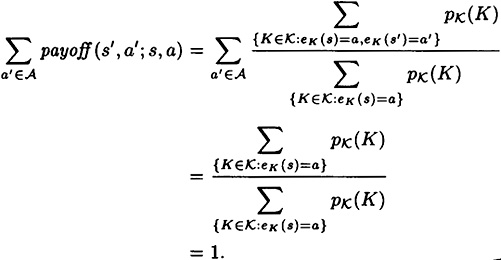
So, there exists an authentication tag a′(s′, s, a) such that

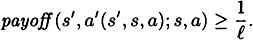
The next theorem follows as a consequence.

THEOREM 10.2

Suppose 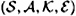is an authentication code. Then 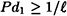, where 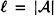. Further, 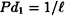if and only if

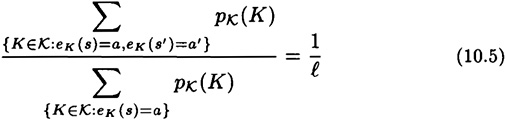
for every .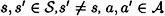

PROOF We have

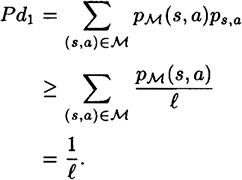
Further, equality occurs if and only if 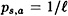for ever (s, a). But this is in turn equivalent to the condition that 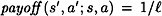for every (s, a).

Combining Theorems 10.1 and 10.2, we get the following:

THEOREM 10.3

Suppose 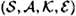is an authentication code, where 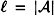. Then 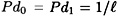if and only if

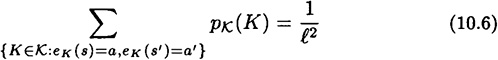
for every .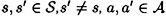

PROOF Equations (10.4) and (10.5) imply Equation (10.6). Conversely, Equation (10.6) implies Equations (10.4) and (10.5).

If the keys are equiprobable, then we obtain the following corollary:

COROLLARY 10.4

Suppose 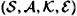is an authentication code where 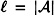, and keys are chosen equiprobably. Then 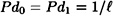if and only if

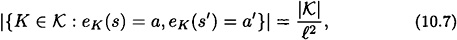
for every .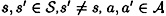

10.3.1 Orthogonal Arrays

In this section, we look at the connections between authentication codes and certain combinatorial structures called orthogonal arrays. First, we give a definition.

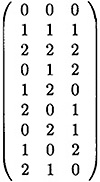
Figure 10.5 An OA(3, 3, 1)

DEFINITION 10.2 An orthogonal array OA(n, k, λ) is a λn² × k array of n symbols, such that in any two columns of the array every one of the possible n² pairs of symbols occurs in exactly λ rows.

Orthogonal arrays are well-studied structures in combinatorial design theory, and are equivalent to other structures such as transversal designs, mutually orthogonal Latin squares and nets.

In Figure 10.5, we present an orthogonal array OA(3, 3, 1) which is obtained from the authentication matrix of Figure 10.3. Any orthogonal array OA(n, k, λ) can be used to construct an authentication code with Pd₀ = Pd₁ = 1/n, as stated in the following theorem.

THEOREM 10.5

Suppose there is an orthogonal array OA(n, k, λ). Then there is an authentication code 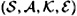, where 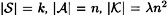and Pd₀ = Pd₁ = 1/n.

PROOF Use each row of the orthogonal array as an authentication rule with equal probability 1/(λn²). The correspondences are as follows:

Since Equation (10.7) is satisfied, we can apply Corollary 10.4, obtaining a code with the stated properties.

Table of Contents