ECONOMETRIC MODELS

In the world of ever-changing demand by the customer, the pressure is on everyone to be able to forecast. Econometric models fill this need. Econometric models, also called causal models, use regression to forecast a time series variable by means of other explanatory time series variables. For example, a company might use a causal model to regress future sales on its advertising level, the population income level, the interest rate, and possibly other variables . Because we have already discussed regression models in some depth, we will not devote much time to econometric models in this chapter; the mechanics are largely the same as in any regression analysis. However, based on the empirical evidence presented in Armstrong (1985, 1986), here are some findings:

It is not necessary to include a lot of explanatory variables in the analysis. It is better to choose a small number of variables that, based on prior evidence, are believed to affect the response variable.
It is important to select the proper conceptual explanatory variables. For example, in forecasting sales, appropriate conceptual variables might be market size , ability to buy, consumer needs, and price. However, the operational measures of these conceptual variables are relatively unimportant for forecast accuracy. For example, different measures of buying power might lead to comparable sales forecasts.
Stepwise regression procedures allow the model builder to search through many possible explanatory variables to find the best model. This sounds good, and it is attractive given the access to powerful statistical software packages. However, it can lead to poor forecasts because it substitutes computer technology for sound judgment and prior theory. The moral is that we should not throw everything but the kitchen sink into the regression package and hope for the best. Some judgment regarding the variables to include may lead to better forecasts.
High precision data on the explanatory variables are not essential. Armstrong (1986) quotes studies where models requiring forecasts of the explanatory variables did better than those where no such forecasts were required. This is contrary to intuition. We might expect that the forecasting error in the explanatory variables would lead to extra forecasting error in the response variable. This is apparently not always the case. However, the same does not hold for the response variable. It is important to have high-quality data on this variable.
It might be a good idea to break the causal relationship into a causal chain of relationships and then estimate each part of the chain by a separate regression equation. For example, in a study of product sales, the first stage of the chain might regress price on such variables as wage rates, taxes, and warranty costs. These price predictions could then be entered into a model that predicts sales per capita as a function of personal consumption expenditures per capita and product price. The third stage could then predict the market size as a function of total population, literacy , age, and employment. Finally, the fourth stage could regress total product sales on the predicted values of product sales per capita and market size.
The divide-and-conquer strategy outlined in the previous point is simpler than the complex simultaneous equation approach taught in many upper-level econometrics courses. The idea behind simultaneous equations is that there are several response (or endogenous) variables that cause changes in one another (Y ₁ causes a change in Y ₂ , which in turn causes a change in Y ₁ , and so on). Therefore, the regression model consists of several equations, each of which has its own response variable. According to Armstrong, despite great expenditures of time and money by the best and brightest econometricians, simultaneous equations have not been found to be of value in forecasting.
The functional form of the relationship may not be terribly important. In particular, complex nonlinear relationships do not appear to improve forecast accuracy. However, in addition to the basic linear additive model, the constant-elasticity multiplicative model

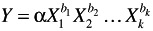
which can be transformed to a linear additive model by taking logarithms, has strong theoretical support and has done well in applications.
A great deal of research has gone into the autocorrelation structure of econometric models. This is difficult analysis for most practitioners . Fortunately, empirical studies show that it produces only marginal gains in forecast accuracy.
Econometric models appear to be most useful, relative to other forecasting methods , when large changes in the explanatory variables are expected. But in this case it is important to be able to forecast the direction of change in the explanatory variables accurately.

Armstrong summarizes his empirical findings on econometric models succinctly: "There are two important rules in the use of econometric methods: (1) keep it simple, and (2) don't make mistakes. If you obey rule 1, rule 2 becomes easier to follow." He acknowledges that rule 1 runs contrary to the thinking of many academic researchers, even practitioners. But the empirical evidence simply does not support the claim that complexity and forecast accuracy are inevitably related .

Now that we have an understanding of some of the limitations, let us explore the econometric models a little deeper. Most of the models in this chapter use only previous values of a time series variable Y to forecast future values of Y. A natural extension is to use one or more other time series variables, via a regression equation, to forecast Y. For example, if a company wants to forecast its monthly sales, it might use its own past advertising levels and/or macroeconomic variables such as Gross Domestic Product (GDP) and the prime interest rate to forecast future sales. We will not study this approach in any detail because it can become quite complex mathematically. However, there are a few points worth making.

Let X be a potential explanatory variable, such as the company's advertising level or GDP. Then either X or any of its lags could be used as explanatory variables in a regression equation for Y. If X itself is included, it is called a coincident indicator of Y _t . If only its lags are included, it is called a leading indicator of Y _t . As an example, suppose that Y _t represents a company's sales during month t and X represents its advertising level during month t. It is certainly plausible that current sales are determined more by past months' advertising levels than by the current month's level. In this case, advertising is a leading indicator of sales, and the advertising terms that should be included in the equation are X _t-1 , X _t-2 , and so on. The number of lags that should be included is difficult to specify ahead of time. In practice, we might begin by including a fairly large number of lags and then discard those with insignificant coefficients in the regression output.

If we decide to use a coincident indicator, the problem is a practical one ” namely, that the value of X is probably not known at the time we are forecasting Y _t . Hence, it must also be forecasted. For example, if we believe that GDP is a coincident indicator of a company's sales, then we must first forecast GDP before we can use it to forecast sales. This may be a more difficult problem than forecasting sales itself. So from a practical point of view, we would like the variables on the right-hand side of the regression equation ” the explanatory variables ” to be known at the time the forecast is being made.

Once we have decided which variables to use as explanatory variables, the analysis itself is carried out exactly as with any other regression analysis, and the diagnostic tools are largely the same as with regression of cross-sectional data. However, there are several things to be aware of.

First, because the explanatory variables are often lagged variables, either of the dependent variables or of some other explanatory variables, we will have to create these lagged variables to use them in the regression equation.

Second, autocorrelation may present problems. Recall that in the least squares estimation procedure, the residuals automatically average to zero. However, autocorrelation of the residuals means that errors in one period are not independent of errors in previous periods. The most common type of residual autocorrelation, positive autocorrelation, implies that if the forecast is on the high side in one period, it is likely to be on the high side the next period. Or if the forecast is on the low side in one period, it is likely to be on the low side the next period. We can detect residual autocorrelation by capturing the residuals and then looking at their autocorrelations to see if any are statistically significant.

Many regression outputs also include the Durbin-Watson statistic to check for lag 1 autocorrelation. The value of this statistic is always between zero and four. If the Durbin-Watson statistic is near two, then autocorrelation is not a problem. However, if it is significantly less than two (as measured by special tables), then there is significant positive autocorrelation, whereas if it is significantly greater than two, there is significant negative autocorrelation. Actually, the Durbin-Watson statistic tests only for autocorrelation of lag 1, not for any higher lags. Therefore, a graph of the autocorrelations (a correlogram) provides more complete information than is contained in the Durbin-Watson statistic alone.

If a regression model does contain significant residual autocorrelation, this is generally a sign that the model is not as good as it could be. Perhaps we have not included the best set of explanatory variables, or perhaps we have not used the best form of the response variable. This is a very complex topic, and we cannot do it justice here. Suffice it to say that a primary objective of any forecasting model, including econometric models, is to end up with uncorrelated residuals. This is easy to say, but it is often difficult to obtain, and we admit that the work necessary to eliminate residual autocorrelation is not always worth the extra effort in terms of more accurate forecasts.

An important final point is that two time series, Y _t and X _t , may be highly correlated and hence produce a promising regression output, even though they are not really related at all. Suppose, for example, that both series are dominated by upward trends through time but are in no way related. Because they are both trending upward, it is very possible that they will have a large positive correlation, which means that the regression of Y _t on X _t has a large R ² value. This is called a spurious correlation because it suggests a relationship that does not really exist. In such a case it is sometimes better to use an extrapolation model to model Y _t and then regress the residuals of Y _t on X _t . Intuitively, we first see how much of the behavior of the Y _t series can be explained by its own past values. Then we regress whatever remains on the X _t series.

We will not pursue this strategy here, but it does suggest how complex a rigorous econometric analysis can be. It is not just a matter of loading Ys and Xs into a computer package and running the "obvious" regression. The output could look good, but it could also be very misleading.