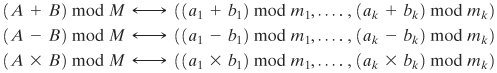[Page 245 (continued)]8.4. The Chinese Remainder Theorem One of the most useful results of number theory is the Chinese remainder theorem (CRT).[7] In essence, the CRT says it is possible to reconstruct integers in a certain range from their residues modulo a set of pairwise relatively prime moduli. [7] The CRT is so called because it is believed to have been discovered by the Chinese mathematician Sun-Tsu in around 100 A.D.
| The 10 integers in Z10, that is the integers 0 through 9, can be reconstructed from their two residues modulo 2 and 5 (the relatively prime factors of 10). Say the known residues of a decimal digit x are r2 = 0 and r5 = 3; that is, x mod 2 =0 and x mod 5 = 3. Therefore, x is an even integer in Z10 whose remainder, on division by 5, is 3. The unique solution is x = 8. |
The CRT can be stated in several ways. We present here a formulation that is most useful from the point of view of this text. An alternative formulation is explored in Problem 8.17. Let 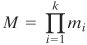
where the mi are pairwise relatively prime; that is, gcd(mi, mj) = 1 for 1  j j  i i 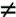 A in ZM by a k-tuple whose elements are in Zmi using the following correspondence: A in ZM by a k-tuple whose elements are in Zmi using the following correspondence: Equation 8-7 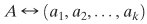
where A 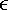 ai ai  ai = A mod mi for 1 ai = A mod mi for 1 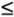
[Page 246]The mapping of Equation (8.7) is a one-to-one correspondence (called a bijection) between ZM and the Cartesian product Zm1 x Zm2 x ... x Zmk. That is, for every integer A such that 0 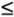 M there is a unique k-tuple (a1, a2,..., ak) with 0 M there is a unique k-tuple (a1, a2,..., ak) with 0 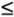 mi that represents it, and for every such k-tuple (a1, a2,..., ak) there is a unique integer A in ZM. mi that represents it, and for every such k-tuple (a1, a2,..., ak) there is a unique integer A in ZM.
Operations performed on the elements of ZM can be equivalently performed on the corresponding k-tuples by performing the operation independently in each coordinate position in the appropriate system. Let us demonstrate the first assertion. The transformation from A to (a1, a1,..., ak) is obviously unique; that is, each ai is uniquely calculated as ai = A mod mi. Computing A from (a1, a1,..., ak) can be done as follows. Let Mi = M/mi for 1 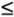 Mi = m1 x m2 x ... x mi-1 x mi+1 x ... x mk so that Mi Mi = m1 x m2 x ... x mi-1 x mi+1 x ... x mk so that Mi  0(mod j 0(mod j 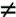 Equation 8-8 Equation 8-8 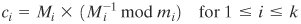
By the definition of Mi it is relatively prime to mi and therefore has a unique multiplicative inverse mod mi So Equation (8.8) is well defined and produces a unique value ci. We can now compute: Equation 8-9 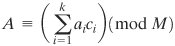
To show that the value of A produced by Equation (8.9) is correct, we must show that ai = A mod mi for 1 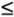 cj cj  0(mod j 0(mod j  ci ci  1(mod ai = A mod mi. 1(mod ai = A mod mi. The second assertion of the CRT, concerning arithmetic operations, follows from the rules for modular arithmetic. That is, the second assertion can be stated as follows: If 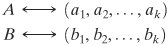
then 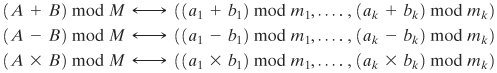
One of the useful features of the Chinese remainder theorem is that it provides a way to manipulate (potentially very large) numbers mod M in terms of tuples of smaller numbers. This can be useful when M is 150 digits or more. However, note that it is necessary to know beforehand the factorization of M.
[Page 247]| To represent 973 mod 1813 as a pair of numbers mod 37 and 49, define[8] m1 = 37 m2 = 49 M = 1813 A = 973 We also have M1 = 49 and M2 = 37. Using the extended Euclidean algorithm, we compute 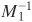 = 34 mod m1 and = 34 mod m1 and 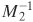 = 4 mod m2. (Note that we only need to compute each Mi and each = 4 mod m2. (Note that we only need to compute each Mi and each 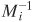 once.) Taking residues modulo 37 and 49, our representation of 973 is (11, 42), because 973 mod 37 = 11 and 973 mod 49 = 42. once.) Taking residues modulo 37 and 49, our representation of 973 is (11, 42), because 973 mod 37 = 11 and 973 mod 49 = 42. Now suppose we want to add 678 to 973. What do we do to (11, 42)? First we compute (678)  (678 mod 37, 678 mod 49) = (12, 41). Then we add the tuples element-wise and reduce (11 + 12 mod 37, 42 + 41 mod 49) = (23, 34). To verify that this has the correct effect, we compute (678 mod 37, 678 mod 49) = (12, 41). Then we add the tuples element-wise and reduce (11 + 12 mod 37, 42 + 41 mod 49) = (23, 34). To verify that this has the correct effect, we compute (23,34)  a1M1 a1M1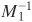 + a2M2 + a2M2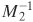 mod M mod M = [(23)(49)(34) + (34)(37)(4)] mod 1813 = 43350 mod 1813 = 1651 and check that it is equal to (973 + 678) mod 1813 = 1651. Remember that in the above derivation, 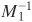 is the multiplicative inverse of M1 modulo m1, and is the multiplicative inverse of M1 modulo m1, and 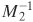 is the multiplicative inverse of M2 modulo m2. is the multiplicative inverse of M2 modulo m2. Suppose we want to multiply 1651 (mod 1813) by 73. We multiply (23, 34) by 73 and reduce to get (23 x 73 mod 37, 34 x 73 mod 49) = (14,32). It is easily verified that (32,14)  [(14)(49)(34) + (32)(37)(4)] mod 1813 [(14)(49)(34) + (32)(37)(4)] mod 1813 = 865 = 1651 x 73 mod 1813 |
[8] This example was provided by Professor Ken Calvert of Georgia Tech.
|
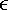
 0(mod
0(mod