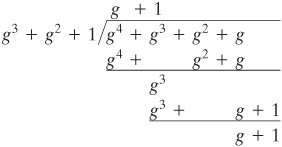[Page 119 (continued)]4.6. Finite Fields Of the Form GF(2n) Earlier in this chapter, we mentioned that the order of a finite field must be of the form pn where p is a prime and n is a positive integer. In Section 4.4, we looked at the special case of finite fields with order p. We found that, using modular arithmetic in Zp, all of the axioms for a field (Figure 4.1) are satisfied. For polynomials over pn, with n > 1, operations modulo pn do not produce a field. In this section, we show what structure satisfies the axioms for a field in a set with pn elements, and concentrate on GF(2n). Motivation Virtually all encryption algorithms, both symmetric and public key, involve arithmetic operations on integers. If one of the operations that is used in the algorithm is division, then we need to work in arithmetic defined over a field. For convenience and for implementation efficiency, we would also like to work with integers that fit exactly into a given number of bits, with no wasted bit patterns. That is, we wish to work with integers in the range 0 through 2n 1, which fit into an n-bit word. | Suppose we wish to define a conventional encryption algorithm that operates on data 8 bits at a time and we wish to perform division. With 8 bits, we can represent integers in the range 0 through 255. However, 256 is not a prime number, so that if arithmetic is performed in Z256 (arithmetic modulo 256), this set of integers will not be a field. The closest prime number less than 256 is 251. Thus, the set Z251, using arithmetic modulo 251, is a field. However, in this case the 8-bit patterns representing the integers 251 through 255 would not be used, resulting in inefficient use of storage. |
As the preceding example points out, if all arithmetic operations are to be used, and we wish to represent a full range of integers in n bits, then arithmetic modulo will not work; equivalently, the set of integers modulo 2n, for n > 1, is not a field. Furthermore, even if the encryption algorithm uses only addition and multiplication, but not division, the use of the set Z2n is questionable, as the following example illustrates.
[Page 120]| Suppose we wish to use 3-bit blocks in our encryption algorithm, and use only the operations of addition and multiplication. Then arithmetic modulo 8 is well defined, as shown in Table 4.1. However, note that in the multiplication table, the nonzero integers do not appear an equal number of times. For example, there are only four occurrences of 3, but twelve occurrences of 4. On the other hand, as was mentioned, there are finite fields of the form GF(2n) so there is in particular a finite field of order 23 = 8. Arithmetic for this field is shown in Table 4.5. In this case, the number of occurrences of the nonzero integers is uniform for multiplication. To summarize, | | Integer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | | | Occurrences in Z8 | 4 | 8 | 4 | 12 | 4 | 8 | 4 | | | Occurrences in GF(23) | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
Table 4.5. Arithmetic in GF(23) (This item is displayed on page 121 in the print version) 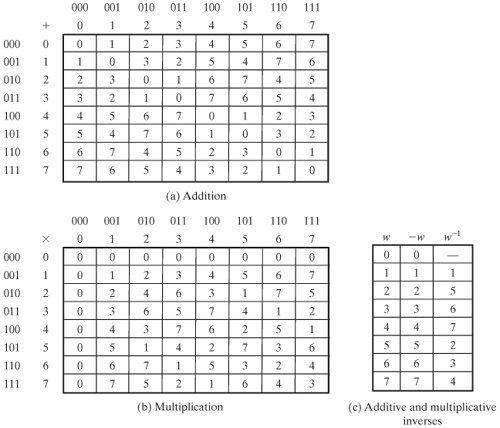
For the moment, let us set aside the question of how the matrices of Table 4.5 were constructed and instead make some observations. The addition and multiplication tables are symmetric about the main diagonal, in conformance to the commutative property of addition and multiplication. This property is also exhibited in Table 4.1, which uses mod 8 arithmetic. All the nonzero elements defined by Table 4.5 have a multiplicative inverse, unlike the case with Table 4.1. The scheme defined by Table 4.5 satisfies all the requirements for a finite field. Thus, we can refer to this scheme as GF(23). For convenience, we show the 3-bit assignment used for each of the elements of GF(23).
|
Intuitively, it would seem that an algorithm that maps the integers unevenly onto themselves might be cryptographically weaker than one that provides a uniform mapping. Thus, the finite fields of the form GF(2n) are attractive for cryptographic algorithms. To summarize, we are looking for a set consisting of 2n elements, together with a definition of addition and multiplication over the set that define a field. We can assign a unique integer in the range 0 through 2n 1 to each element of the set. Keep in mind that we will not use modular arithmetic, as we have seen that this does not result in a field. Instead, we will show how polynomial arithmetic provides a means for constructing the desired field. Modular Polynomial Arithmetic Consider the set S of all polynomials of degree n 1 or less over the field Zp. Thus, each polynomial has the form 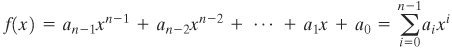
where each ai takes on a value in the set {0, 1,..., p 1}. There are a total of pn different polynomials in S.
[Page 121]For p = 3 and n = 2, the 32 = 9 polynomials in the set are | 0 | x | 2x | 1 | x + 1 | 2x + 1 | 2 | x + 2 | 2x + 2 | For p = 2 and n = 3, the 23 = 8 the polynomials in the set are | 0 | x + 1 | x2 + x | 1 | x2 | x2 + x + 1 | x | x2 + 1 | |
With the appropriate definition of arithmetic operations, each such set S is a finite field. The definition consists of the following elements: Arithmetic follows the ordinary rules of polynomial arithmetic using the basic rules of algebra, with the following two refinements. Arithmetic on the coefficients is performed modulo p. That is, we use the rules of arithmetic for the finite field Zp.
[Page 122]If multiplication results in a polynomial of degree greater than n 1, then the polynomial is reduced modulo some irreducible polynomial m(x) of degree n. That is, we divide by m(x) and keep the remainder. For a polynomial f(x), the remainder is expressed as r(x) = f(x) mod m(x).
| The Advanced Encryption Standard (AES) uses arithmetic in the finite field GF(28), with the irreducible polynomial m(x) = x8 + x4 x3 + x + 1. Consider the two polynomials f(x) = x6 + x4 + x2 + x + 1 and g(x) = x7 + x + 1. Then f(x) + g(x) = x6 + x4 x2 + x + 1 + x7 + x + 1 f(x) x g(x) = x13 + x11 + x9 + x8 + x7 + x7 + x5 + x3 + x2 + x + x6 + x4 + x2 + x + 1 = x13 + x11 + x9 + x8 + x6 + x5 + x4 + x3 + 1 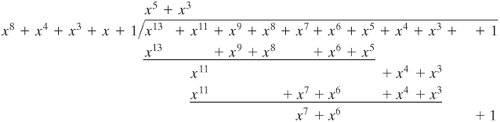
Therefore, f(x) x g(x) mod m(x) = x7 + x6 + 1. |
As with ordinary modular arithmetic, we have the notion of a set of residues in modular polynomial arithmetic. The set of residues modulo m(x), an nth-degree polynomial, consists of pn elements. Each of these elements is represented by one of the pn polynomials of degree m < n. | The residue class [x + 1], modulo m(x), consists of all polynomials a(x) such that a(x) 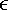 (m(x)). Equivalently, the residue class [x + 1] consists of all polynomials a(x) that satisfy the equality a(x) mod m(x) = x + 1. (m(x)). Equivalently, the residue class [x + 1] consists of all polynomials a(x) that satisfy the equality a(x) mod m(x) = x + 1. |
It can be shown that the set of all polynomials modulo an irreducible nth-degree polynomial m(x) satisfies the axioms in Figure 4.1, and thus forms a finite field. Furthermore, all finite fields of a given order are isomorphic; that is, any two finite-field structures of a given order have the same structure, but the representation, or labels, of the elements may be different.
[Page 123]| To construct the finite field GF(23), we need to choose an irreducible polynomial of degree 3. There are only two such polynomials: (x3 + x2 + 1) and (x3 + x + 1). Using the latter, Table 4.6 shows the addition and multiplication tables for GF(23). Note that this set of tables has the identical structure to those of Table 4.5. Thus, we have succeeded in finding a way to define a field of order 23. Table 4.6. Polynomial Arithmetic Modulo (x3 + x + 1) (This item is displayed on page 124 in the print version) 
|
Finding the Multiplicative Inverse Just as the Euclidean algorithm can be adapted to find the greatest common divisor of two polynomials, the extended Euclidean algorithm can be adapted to find the multiplicative inverse of a polynomial. Specifically, the algorithm will find the multiplicative inverse of b(x) modulo m(x) if the degree of b(x) is less than the degree of m(x) and gcd[m(x), b(x)] = 1. If m(x) is an irreducible polynomial, then it has no factor other than itself or 1, so that gcd[m(x), b(x)] = 1. The algorithm is as follows: EXTENDED EUCLID[m(x), b(x)] 1. [A1(x), A2(x), A3(x)]  [1, 0, x)]; [B1(x), B2(x), B3(x)] [1, 0, x)]; [B1(x), B2(x), B3(x)]  [0, 1, x)] 2. if B3(x) = 0 return A3(x) = gcd[m(x), b(x)]; no inverse 3. if B3(x) = 1 return B3(x) = gcd[m(x), b(x)]; B2(x) = b(x)1 mod m(x) 4. Q(x) = quotient of A3(x)/B3(x) 5. [T1(x), T2(x), T3(x)] [0, 1, x)] 2. if B3(x) = 0 return A3(x) = gcd[m(x), b(x)]; no inverse 3. if B3(x) = 1 return B3(x) = gcd[m(x), b(x)]; B2(x) = b(x)1 mod m(x) 4. Q(x) = quotient of A3(x)/B3(x) 5. [T1(x), T2(x), T3(x)]  [A1(x)B1(x), A2(x) Q(x)B2(x), A3(x) QB3(x)] 6. [A1(x), A2(x), A3(x)] [A1(x)B1(x), A2(x) Q(x)B2(x), A3(x) QB3(x)] 6. [A1(x), A2(x), A3(x)]  [B1(x), B3(x)] 7. [B1(x), B2(x), B3(x)] [B1(x), B3(x)] 7. [B1(x), B2(x), B3(x)]  [T1(x), T3(x)] 8. goto 2 [T1(x), T3(x)] 8. goto 2
| Table 4.7 shows the calculation of the multiplicative inverse of (x7 + x + 1) mod (x8 + x4 + x3 + x + 1). The result is that (x7 + x + 1)1 = (x7). That is, (x7 + x + 1)(x7)  1 (mod (x4 + x3 + x + 1)). 1 (mod (x4 + x3 + x + 1)). Table 4.7. Extended Euclid [(x8 + x4 + x3 + x + 1), (x7 + x + 1)] (This item is displayed on page 125 in the print version) Initialization | A1(x) = 1; A2(x) = 0; A3(x) = x8 + x4 + x3 + x + 1
B1(x) = 0; B2(x) = 1; B3(x) = x7 + x + 1 | Iteration 1 | Q(x) = x
A1(x) = 0; A2(x) = 1; A3(x) = x7 + x + 1
B1(x) = 1; B2(x) = x; B3(x) = x4 + x3 + x2 + 1 | Iteration 2 | Q(x) = x3 + x2 + 1
A1(x) = 1; A2(x) = x; A3(x) = x4 + x3 + x2 + 1
B1(x) = x3 + x2 + 1; B2(x) = x4 + x3 + x + 1; B3(x) = x | Iteration 3 | Q(x) = x3 + x2 + x
A1(x) = x3 + x2 + 1; A2(x) = x4 + x3 + x + 1; A3(x) = x
B1(x) = x6 + x2 + x + 1; B2(x) = x7; B3(x) = 1 | Iteration 4 | B3(x) = gcd[(x7 + x + 1), (x8 + x4 + x3 + x + 1)] = 1
B2(x) = (x7 + x + 1)1 mod (x8 + x4 + x3 + x + 1) = x7 |
|
Computational Considerations A polynomial f(x) in GF(2n) 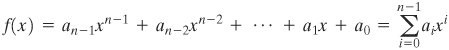
can be uniquely represented by its n binary coefficients (an1an2...a0). Thus, every polynomial in GF(2n) can be represented by an n-bit number.
[Page 125]| Tables 4.5 and 4.6 show the addition and multiplication tables for GF(23) modulo m(x) = (x3 + x + 1). Table 4.5 uses the binary representation, and Table 4.6 uses the polynomial representation. |
Addition We have seen that addition of polynomials is performed by adding corresponding coefficients, and, in the case of polynomials over Z2 addition is just the XOR operation. So, addition of two polynomials in GF(2n) corresponds to a bitwise XOR operation. | Consider the two polynomials in GF(28) from our earlier example: f(x) = x6 + x4 + x2 + x + 1 and g(x) = x7 + x + 1. (x6 + x4 + x2 + x + 1) + (x7+ x + 1) | = x7 + x6 + x6 + x4 + x2 | (polynomial notation) | (01010111)  (10000011) (10000011) | = (11010100) | (binary notation) | {57}  {83} {83} | = {D4} | (hexadecimal notation)[7] |
[7] A basic refresher on number systems (decimal, binary, hexadecimal) can be found at the Computer Science Student Resource Site at WilliamStallings.com/StudentSupport.html. Here each of two groups of 4 bits in a byte is denoted by a single hexadecimal character, the two characters enclosed in brackets.
|
Multiplication There is no simple XOR operation that will accomplish multiplication in GF(2n) However, a reasonably straightforward, easily implemented technique is available. We will discuss the technique with reference to GF(28) using m(x) = x8 + x4 + x3 + x + 1, which is the finite field used in AES. The technique readily generalizes to GF(2n). The technique is based on the observation that Equation 4-8 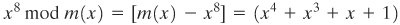
[Page 126]A moment's thought should convince you that Equation (4.8) is true; if not, divide it out. In general, in GF(2n) with an nth-degree polynomial p(x), we have xn mod p(x) = [p(x) xn]. Now, consider a polynomial in GF(28), which has the form f(x) = b7x7 + b6x6 + b5x5 + b4x4 + b3x3 + b2x2 + b1x + b0. If we multiply by x, we have Equation 4-9 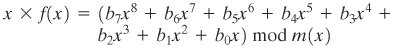
If b7 = 0, then the result is a polynomial of degree less than 8, which is already in reduced form, and no further computation is necessary. If b7 = 1, then reduction modulo m(x) is achieved using Equation (4.8): x x f(x) = (b6x7 + b5x6 + b4x5 + b3x4 + b2x3 + b1x2 + b0x) + (x4 + x3 + x + 1) It follows that multiplication by x (i.e., 00000010) can be implemented as a 1-bit left shift followed by a conditional bitwise XOR with (00011011), which represents (x4 + x3 + x + 1). To summarize, Equation 4-10 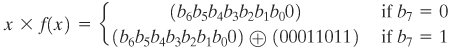
Multiplication by a higher power of x can be achieved by repeated application of Equation (4.10). By adding intermediate results, multiplication by any constant in GF(28) can be achieved. | In an earlier example, we showed that for f(x) = x6 + x4 + x2 + x + 1, g(x) = x7 + x + 1, and m(x) = x8 + x4 + x3 + x + 1, f(x) x g(x) mod m(x) = x7 + x6 + 1. Redoing this in binary arithmetic, we need to compute (01010111) x (10000011). First, we determine the results of multiplication by powers of x: (01010111) x (00000001) = (10101110) (01010111) x (00000100) = (01011100)  (00011011) = (01000111) (00011011) = (01000111) (01010111) x (00001000) = (10001110) (01010111) x (00010000) = (00011100)  (00011011) = (00000111) (00011011) = (00000111) (01010111) x (00100000) = (00001110) (01010111) x (01000000) = (00011100) (01010111) x (10000000) = (00111000) So, (01010111) x (10000011) = (01010111) x [(00000001) x (00000010) x (10000000)] = (01010111)  (10101110) (10101110)  (00111000) = (11000001) (00111000) = (11000001) which is equivalent to x7 + x6 + 1. |
[Page 127]Using a Generator An equivalent technique for defining a finite field of the form GF(2n) using the same irreducible polynomial, is sometimes more convenient. To begin, we need two definitions: A generator g of a finite field F of order q (contains q elements) is an element whose first q 1 powers generate all the nonzero elements of F. That is, the elements of F consist of 0, g0, g1,..., gq2. Consider a field F defined by a polynomial f(x). An element b contained in F is called a root of the polynomial if f(b) = 0. Finally, it can be shown that a root g of an irreducible polynomial is a generator of the finite field defined on that polynomial. | Let us consider the finite field GF(23), defined over the irreducible polynomial x3 + x + 1, discussed previously. Thus, the generator g must satisfy f(x) = g3 + g + 1 = 0. Keep in mind, as discussed previously, that we need not find a numerical solution to this equality. Rather, we deal with polynomial arithmetic in which arithmetic on the coefficients is performed modulo 2. Therefore, the solution to the preceding equality is g3 = g 1 = g + 1. We now show that g in fact generates all of the polynomials of degree less than 3. We have the following: g4 = g(g3) = g(g + 1) = g2 + g g5 = g(g4) = g(g2 + g) = g3 + g2 = g2 + g + 1 g6 = g(g5) = g(g2 + g + 1) = g3 + g2 + g = g2 + g + g + 1 = g2 + 1 g7 = g(g6) = g(g2 + 1) = g3 + g = g + g + 1 = 1 = g0 We see that the powers of g generate all the nonzero polynomials in GF(23). Also, it should be clear that gk = gk mod 7 for any integer k. Table 4.8 shows the power representation, as well as the polynomial and binary representations. Table 4.8. Generator for GF(23) using x3 + x + 1Power Representation | Polynomial Representation | Binary Representation | Decimal (Hex) Representation |
|---|
0 | 0 | 000 | 0 | g0 ( = g7) | 1 | 001 | 1 | g1 | g | 010 | 2 | g2 | g2 | 100 | 4 | g3 | g + 1 | 011 | 3 | g4 | g2 + g | 110 | 6 | g5 | g2 + g + 1 | 111 | 7 | g6 | g2 + 1 | 101 | 5 |
This power representation makes multiplication easy. To multiply in the power notation, add exponents modulo 7. For example, g4 x g6 = g(10 mod 7) = g3 = g + 1. The same result is achieved using polynomial arithmetic, as follows: we have g4 = g2 + g and g6 = g2 + 1. Then, (g2 + g) x (g2 + 1) = g4 + g3 + g2 + 1. Next, we need to determine (g4 + g3 + g2 + 1) mod (g3 + g + 1) by division:
[Page 129] 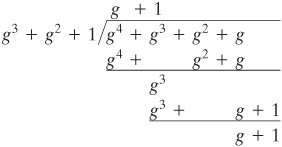
We get a result of g + 1, which agrees with the result obtained using the power representation. Table 4.9 shows the addition and multiplication tables for GF(23) using the power represenation. Note that this yields the identical results to the polynomial representation (Table 4.6) with some of the rows and columns interchanged. Table 4.9. GF(23) Arithmetic Using Generator for the Polynomial (x3 + x + 1) (This item is displayed on page 128 in the print version) 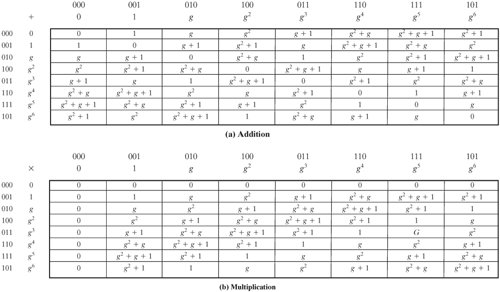
|
In general, for GF(2n) with irreducible polynomial f(x), determine gn = f(x) gn. Then calculate all of the powers of g from gn+1 through g2n2. The elements of the field correspond to the powers of g from through g2n2, plus the value 0. For multiplication of two elements in the field, use the equality gk = gk mod (2n1) for any integer k. Summary In this section, we have shown how to construct a finite field of order 2n. Specifically, we defined GF(2n) with the following properties: GF(2n) consists of 2n elements. The binary operations + and x are defined over the set. The operations of addition, subtraction, multiplication, and division can be performed without leaving the set. Each element of the set other than 0 has a multiplicative inverse.
We have shown that the elements of GF(2n) can be defined as the set of all polynomials of degree n 1 or less with binary coefficients. Each such polynomial can be represented by a unique n-bit value. Arithmetic is defined as polynomial arithmetic modulo some irreducible polynomial of degree n. We have also seen that an equivalent definition of a finite field GF(2n) makes use of a generator and that arithmetic is defined using powers of the generator. |


 (
(
 [1, 0,
[1, 0,  1 (mod (
1 (mod (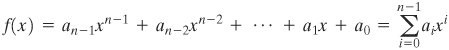
 (10000011)
(10000011)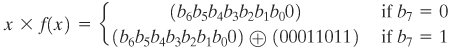
 (00011011) = (01000111)
(00011011) = (01000111)