Chapter 4,
| < Day Day Up > |
Chapter 4, "Vector Operations"Vector Versus ScalarScalar = magnitude only. Vector = magnitude + direction. DisplacementDisplacement = final position “ initial position. D x = x f “ x i Polar CoordinatesVector where Cartesian Coordinates (Components) Vector where Converting from Polar to Cartesian Coordinates For vector where a 1 = Converting from Cartesian to Polar Coordinates For vector Cartesian Coordinates (Components) in 3D Vector where Commutative Law of Vector AdditionA + B = B + A for any vectors A and B. Adding 2D Vectors Numerically for vectors Adding 3D Vectors Numerically for vectors Subtracting Vectors Numerically for vectors Subtracting 3D Vectors Numerically for vectors Scalar Multiplication in Polar Coordinates for any scalar c and vector Scalar Multiplication in Cartesian Coordinates for any scalar c and vector Normalizing a 2D Vector for any vector A = [ a 1 a 2 ]. Normalizing a 3D Vector for any vector A = [ a 1 a 2 a 3 ]. Dot Product in 2DA B = a 1 b 1 + a 2 b 2 for any 2D vectors A = [ a 1 a 2 ] and B = [ b 1 b 2 ]. Dot Product in 3DA B = a 1 b 1 + a 2 b 2 + a 3 b 3 for any 3D vectors A = [ a 1 a 2 a 3 ] and B = [ b 1 b 2 b 3 ]. Perpendicular Check If A B = 0, A Positive or Negative Dot ProductIf A B < 0 (negative), q > 90 ° If A B > 0 (positive), q < 90 ° where q is the angle between vectors A and B. Angle Between Two Vectors where q is the angle between vectors A and B. Cross-ProductA x B = [( a 2 b 3 “ a 3 b 2 ) ( a 3 b 1 “ a 1 b 3 ) ( a 1 b 2 “ a 2 b 1 )] for any two vectors A = [ a 1 a 2 a 3 ] and B = [ b 1 b 2 b 3 ]. Perpendicular VectorsA x B is perpendicular to both vectors A and B. Cross-Product Is Not Commutative A x B In fact, A x B = “(B x A) for any two 3D vectors A and B. Surface Normal Surface normal = for any two 3D vectors A and B. Angle Between Two Vectors for any two 3D vectors A and B. |
| < Day Day Up > |
EAN: 2147483647
Pages: 143
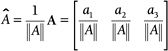
 B.
B.  B x A
B x A