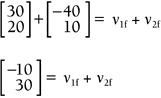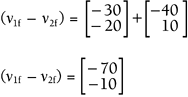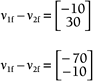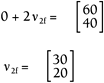Modeling Collisions
| < Day Day Up > |
| The last section took a one-sided approach by looking at the effects of a collision on just one object using the impulse-momentum theorem. Now let's look at the effects on both objects involved in the collision. If two objects collide, and both can move, they both apply an impulse to each other due to the collision. Let's look at the impulse-momentum theorem one more time: Ft = ( D p ) Let's divide both sides by time: F = ( D p )/ t Newton's Third Law states that for every action there's an equal and opposite reaction. In this case, one object places a force on another object, and at the same time, the second object places an equal and opposite force on the first object: F 1 = F 2 Now let's substitute the impulse-momentum theorem on both sides: ( D p 1 )/ t = ( D p 2 )/ t , or D p 1 = D p 2 Now let's insert the definition of momentum on both sides: m 1 v 1f m 1 v 1i = ( m 2 v 2f m 2 v 2i ) m 1 v 1f m 1 v 1i = m 2 v 2f + m 2 v 2i m 1 v 1i + m 2 v 2i = m 1 v 1f + m 2 v 2f This last line has a special name : conservation of momentum theorem . This theorem states that the total amount of momentum stays the same when two objects collide. It simply transfers from one object to the other.
This theorem applies to any isolated collision between two objects. If an outside force interferes with the collision, the theorem no longer holds up. However, due to the speed at which a collision occurs, very rarely does another force interfere. NOTE Remember that momentum is a vector quantity, so this theorem works the same way whether the collision occurs in 1D, 2D, or 3D. Example 13.7: Conservation of Momentum TheoremSuppose you're coding a 3D pool game, and you're focused on the cue ball hitting another ball at rest. If the cue ball has a mass of 0.5kg and an initial velocity of [50 10 30], and it completely stops when it hits the other ball with a mass of 0.45kg, what should the final velocity of the second ball be as a result of the collision? SolutionGo straight to the conservation of momentum theorem, and fill in everything you know: m 1 v 1i + m 2 v 2i = m 1 v 1f + m 2 v 2f You can see that all the cue ball's momentum is transferred to the second ball when they collide. Let's see this converted into a programming function: vector3D conserveMomentum(vector3D object1Start,vector3D object1Stop, vector3D object2Start, float mass1, float mass2) { vector3D temp,temp2,sum,result; //First calculate the left hand side of the equation. temp = scalarMultiply(mass1,object1Start); temp2 = scalarMultiply(mass2,object2Start); sum = sumVectors(temp,temp2); //Divide the left hand side by the second object's mass to //get the vector; result = scalarDivide(mass2,sum); return result; } Using this function, we can find out the final vector of the second object after the collision. This function is used in the provided sample code and is capable of taking different start and stop vectors for the objects. This is a simple example. However, it's quite possible that both objects will move together as a result of the collision. Let's look at such an example. Example 13.8: Perfectly Inelastic CollisionSuppose you're coding a 2D football game with a top-down view. The player with the ball weighs 180lbs and is running down the field toward the end zone with a velocity of [0 30]. One of his opponents, who weighs 220lbs, is on the other side of the field when he starts running at [25 5] to make the tackle. After he makes the tackle, what is the players' final velocity as they go flying across the field together as a result of the tackle? Solution
The only reason you can calculate the final velocities is because they are the same. There's one more case to considerwhen both objects are moving as a result of the collision but they have different final velocities. If you have two unknown variables , v 1f and v 2f , you need a second equation to calculate both. This takes you back to Chapter 1, where you looked at linear combination and substitution. If you think of v 1f as x and v 2f as y , it's actually the same process. Use linear combination or substitution to find one final velocity, and then plug it in to find the other final velocity. To help you find that second equation, we need to discuss different types of collisions. Every collision falls somewhere along a spectrum where one extreme is the elastic collision and the other extreme is the perfectly inelastic collision . An elastic collision is one in which no kinetic energy is lost when the two objects hit. The result is a collision where the objects appear to just bounce off each other like billiard balls. Example 13.8 showed a perfectly inelastic collision, where two objects stuck together and had the same final velocity. In real life, most collisions fall somewhere in between: Some energy is lost, but the two objects have different final velocities. You control how much energy is lost by defining a variable called the coefficient of restitution (
Let's look at this formula more closely. If you plug in 0 for Example 13.9: Elastic CollisionSuppose you're coding a 2D pool game with a top-down view, and you're focused on the elastic collision of two identical billiard balls. If one ball has an initial velocity of [30 20] and the other has an initial velocity of [40 10] when they hit on center, what must their final velocities be? Solution
Note that the two balls transfer momentum because it is elastic. Imagine what might happen if you made Here is a look at elastic collision in code. This function will process the final velocity of two objects with the same mass given the current vectors of each. In this particular example, we have defined restitution at 1 like this: #define RESTITUTION 1 void elasticCollision(vector2D object1, vector2D object2, float mass) { vector2D object1Temp,object2Temp, sum, sum2, object1Velocity,object2Velocity,temp; //First calculate the left hand side of the equation. object1Temp = scalarMultiply(mass,object1); object2Temp = scalarMultiply(mass,object2); sum = sumVectors(object1Temp,object2Temp); //setup right side of equation; multiply through by //restitution value. //This is only for illustration purposes in this example. object1Temp = scalarMultiply(RESTITUTION,object1Temp); object2Temp = scalarMultiply(RESTITUTION,object2Temp); //for example purposes, since the equation switched to // the right side. object1Temp = scalarMultiply(-1,object1Temp); sum2 = sumVectors(object1Temp,object2Temp); //Now we have the two vectors we will need to complete the //solution and calculate the vectors. temp = subtractVectors(sum,sum2); object2Velocity = scalarDivide(2,temp); object1Velocity = subtractVectors(sum,object2Velocity); //print the resulting velocities cout<<"The first object's resulting velocity vector is "; printVector(object1Velocity); cout<<"The second object's resulting velocity vector is \n"; printVector(object2Velocity); } Here, we immediately multiply both vectors by the coefficient of restitution. As you can see, we then follow through completing the equation to solve for the final velocity. This function will give us our answer but is fairly limited to solving one kind of problem. At this point, you have a solid foundation to start experimenting with different types of collisions. The next section shows you how one programmer took this foundation and ran with it to make a remarkably realistic pool simulation. Self-Assessment
|
| < Day Day Up > |
EAN: 2147483647
Pages: 143

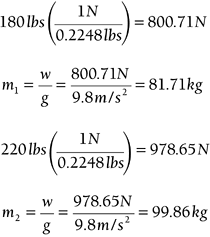
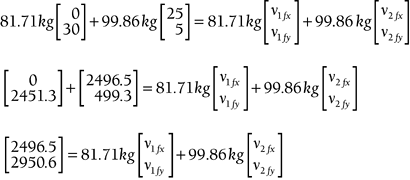
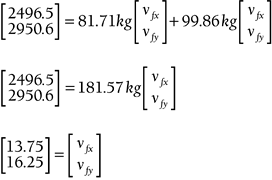
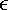 ). For an elastic collision,
). For an elastic collision,