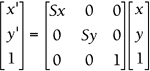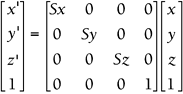Scaling

Matrix multiplication can also be used to scale objects in your game. Just like translation, if you scale each individual vertex, you end up scaling the whole object. Let's set up another matrix equation for scaling. Again, we'll start with 2D and then extend to 3D.

2D Scaling

where Sx = scale factor in the x direction and Sy = scale factor in the y direction.

As soon as you plug in the scale factors ( Sx and Sy ), the process is the same as translation: Plug in each vertex one at a time, and multiply the matrices to find its new location. If you want to perform a uniform scale to keep the proportions the same, just make sure that Sx = Sy . You don't have to perform a uniform scale, however. If you plug in two different values for Sx and Sy , you'll end up with a differential scale .

When choosing values for Sx and Sy , keep in mind that any number between 0 and 1 makes objects smaller, and any number greater than 1 scales objects larger. (Negative values flip the object into a different quadrant.) Let's look at a couple examples.

Example 6.5: 2D Uniform Scale

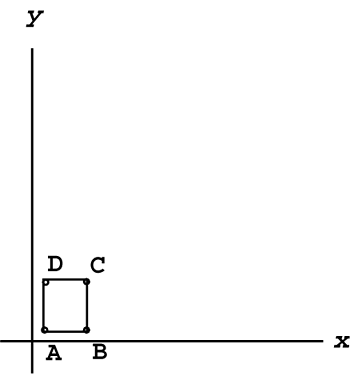
Set up a general matrix equation that will uniformly scale 2D objects 3 times larger, and then use it to scale the rectangle pictured in Figure 6.2.

Figure 6.2. A rectangle to be uniformly scaled.

Solution

1. Set up the matrix equation. To uniformly scale objects 3 times larger, both scale factors must be equal to 3:

   

   
   

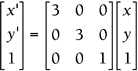
2. Now you have to plug in each old point and multiply the matrices to find the new location. First, plug in the old location of vertex A(10,10):

   

   
   

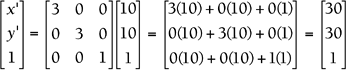
   So A' is the point (30,30).

3. If you repeat step 2 with the old locations of B, C, and D, you get the new locations B'(150,30), C'(150,120), and D'(30,120). By scaling all four vertices, you have scaled the whole rectangle 3 times larger.

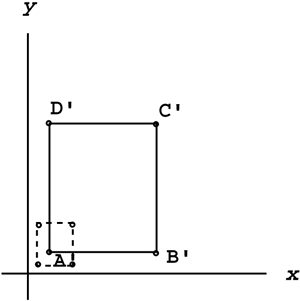
4. The old location and the new location are graphed in Figure 6.3.

   Figure 6.3. Old and new locations of a uniformly scaled rectangle.

   

Turning this into code isn't very difficult, but extends slightly as we try to make something more of it. Here is a function that will take a matrix and multiply the value by a scale passed to it:

 Matrix3X1 scale2DByMultiplication(Matrix3X1 start, float dx, float dy)      {          Matrix3X3 temp;          Matrix3X1 result;          //Zero out the matrix.          temp = createFixed3X3Matrix(0);          //setup the 3x3 for multiplication;          temp.index[0][0] = dx;          temp.index[1][1] = dy;          temp.index[2][2] = 1;          result = multiplyMatrixNxM(temp,start);          return result;      } 

Notice that this function will scale uniformly or nonuniformly based on the values passed through to dx and dy . If you want to make it scale uniformly, just ask for a single scale factor and assign them to be equal.

This is great for scaling up single points, but most objects that are scaled are of some geometric shape. Let's look at part of the driver function from the sample code that indicates how to scale a rectangle uniformly:

 void scale2D()     {       Matrix3X1 start,temp;       float dx,dy, height,width;  cout<<"Please enter the coordinates and dimensions  of a rectangle.\n";       cout<<"X coordinates\n";       cin>>start.index[0];       cout<<"Now the Y coordinate.\n";       cin>>start.index[1];       cout<<"Enter the rectangle's height.\n";       cin>>height;       cout<<"Enter the rectangle's width.\n";       cin>>width;       //make sure the last part of the matrix is a 1.       start.index[2] = 1;       cout<<endl;       cout<<"Now enter the amount to scale by.\n";       cin>>dx;       dy = dx;       temp = scale2DByMultiplication(start,dx,dy);       width = temp.index[0]+width;       height = temp.index[1]+height;       cout<<"The new position is "<<temp.index[0]<<","<<temp.index[1]<<"\n";       cout<<"The right coord is "<<width<<","<<temp.index[1]<<"\n";       cout<<"The bottom coord is "<<height<<","<<temp.index[0]<<"\n";      } 

This function will give the scaled position of all the points in the rectangle and is much more useful than just scaling a single point. We will look at a similar example when we focus on rotation a little later in this chapter.

Look at Figure 6.3 for a moment. Notice that the dimensions of the rectangle are indeed 3 times larger. However, the rectangle appears to have also moved away from the origin. Unfortunately, the scaling matrix is set up to scale objects with respect to the origin, which is why the rectangle moved away from the origin when it was scaled larger. If you had scaled it down, the rectangle would have moved closer to the origin. Unfortunately, if you want to keep the object in the same place and scale it (with respect to its own center), that is a combo. We'll examine that particular combo later in this chapter. In the meantime, let's look at an example of differential scaling with respect to the origin.

NOTE

One way to deal with this issue is to set up a local coordinate system with its own origin. For example, if I'm scaling a human figure who's standing on the ground, I can place the local origin on the soles of the figure's shoes and center it on the other two axes. Then a single scaling matrix would allow the figure to grow from the ground without moving laterally. Quite often, assets that look perfect in the preview applications get sent back to the artist after they start running in the game because their origins were misplaced.

Example 6.6: 2D Differential Scale

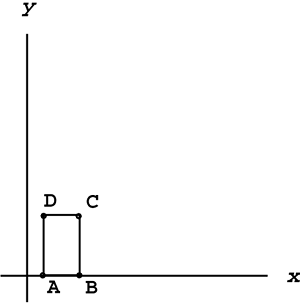
Suppose you have a rectangular-shaped object (see Figure 6.4) with vertices at A(20,0), B(50,0), C(50,100), and D(20,100), and a huge boulder falls on it. You want the object to look like it got squished , so set up a matrix equation that will scale objects 1.5 times in the x direction and 0.1 in the y direction, and then use it to scale the rectangle.

Figure 6.4. A rectangle to be differentially scaled.

Solution

1. Set up the matrix equation. In this case, the scale factor in the x direction is 1.5 and the scale factor in the y direction is 0.1:

   

   
   

2. Now you have to plug in each old point and multiply the matrices to find the new location. First, plug in the old location of vertex A(20,0):

   

   
   

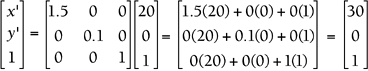
   So A' is the point (30,0).

3. If you repeat step 2 with the old locations of B, C, and D, you get the new locations B'(75,0), C'(75,10), and D'(30,10). By scaling all four vertices, you have scaled the whole rectangle.

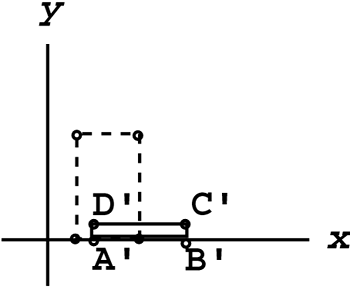
4. The old location and the new location are graphed in Figure 6.5. Notice that the rectangle has become wider and flatter.

   Figure 6.5. Old and new locations of a differentially scaled rectangle.

   

The scaling process works the exact same way in 3D. You just need to add an extra dimension to each matrix in the equation.

3D Scaling

where Sx = scale factor in the x direction, Sy = scale factor in the y direction, and Sz = scale factor in the z direction.

Example 6.7: 3D Uniform Scale

Set up a general matrix equation that will uniformly scale 3D objects 5 times larger, and then use it to scale a triangle with vertices at A(50,0,10), B(0,20,100), and C(200,150,50).

Solution

1. Set up the matrix equation. To uniformly scale objects 5 times larger, all three scale factors must be equal to 5:

   

   
   

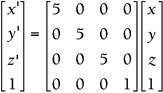
2. Plug in each old point, and multiply the matrices to find the new location. First, plug in the old location of vertex A(50,0,10):

   

   
   

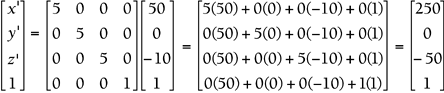
   So A' is the point (250,0,50).

3. If you repeat step 2 with the old locations of B and C, you get the new locations B'(0,100,500) and C'(1000,750,250). By scaling all three vertices, you have scaled the whole triangle 5 times larger.

You can also perform differential scaling in 3D, so let's look at an example of that.

Example 6.8: 3D Differential Scale

Set up a general matrix equation that will scale 3D objects two times taller and half as deep ( z direction), and then use it to scale a triangle with vertices at A(50,0,10), B(0,20,100), and C(200,150,50).

Solution

1. Set up the matrix equation. To scale objects two times taller and half as deep, the scale factor in the x direction must be 1 (no change), the scale factor in the y direction must be 2, and the scale factor in the z direction must be 0.5:

   

   
   

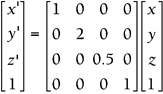
2. Now you have to plug in each old point and multiply the matrices to find the new location. First, plug in the old location of vertex A(50,0,10):

   

   
   

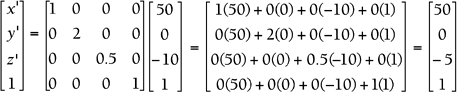
   So A' is the point (50,0,5).

3. If you repeat step 2 with the old locations of B and C, you get the new locations B'(0,40,50) and C'(200,300,25). By scaling all three vertices, you have scaled the whole triangle.

Earlier, we saw a function that could process uniform and non-uniform 2D scaling. Here is a function that works the exact same way for 3D scaling:

 Matrix4X1 scale3DByMultiply(Matrix4X1 start, float dx, float dy, float dz)     {          Matrix4X4 temp;          Matrix4X1 result;          //Zero out the matrix to make sure nothing is left uninitialized.          temp = createFixed4X4Matrix(0);          //setup the 3x3 for multiplication;          temp.index[0][0] = dx;          temp.index[1][1] = dy;          temp.index[2][2] = dz;          temp.index[3][3] = 1;          result = multiplyMatrixNxM(temp,start);          return result;     } 

This operation is performed the same way as the 2D scale function with the addition of a new variable in the form of dz . If you want this function to perform a uniform scale on a point or group of points, ask the user for one scale factor and assign the same value to dx , dy , and dz . The provided sample code for this chapter demonstrates this technique to rotate a set of vertices. Be sure to check it out!

Notice that the process for scaling objects is very similar to that of translating by matrix multiplication. This will make it easy to combine translation and scaling later in this chapter. In the meantime, practice scaling 2D and 3D objects with respect to the origin. This will make the combo of scaling with respect to any other point much easier when you get there.

Self-Assessment

1.

Set up a general matrix equation that will uniformly scale 2D objects in half, and then use it to scale a triangle with vertices at A(50,20), B(10,20), and C(30,40).

2.

Set up a general matrix equation that will make objects tall and skinny by scaling