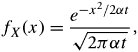Section C.4. Stochastic (Random) Processes

C.4. Stochastic (Random) Processes

A stochastic (random) process is a special version of a random variable that is a function of time. When time is countable, a stochastic process is called discrete time and denoted by X ( n , ‰ ), or X ( n ), or simply X _n , where n is time. Otherwise, a stochastic process is continuous time and is denoted by X ( t ), where t is time.

C.4.1. IID Random Process

As an example of discrete-time random processes, consider the independent and identically distributed (IID) random process . This discrete-time random process is denoted by X _n , in which n "independent" discrete random variables have "identical" CDFs. Therefore, the n random variables X ₁ , occurring at time 1, all the way to X _n , occurring at time n , make up the random process X _n ={ X ₁ , X ₂ , ... , X _n }.

C.4.2. Brownian Motion Random Process

The Brownian motion random process , also called Wiener random process , is an example of continuous-time random processes. A Brownian motion process, X ( t ), begins at the origin, has zero expected value for all time t , but has a variance that increases linearly with time as

Equation C.31

and

Equation C.32

The PDF of a Brownian motion random process can be approximated by the PDF of a Gaussian (normal) random variable presented in Equation (C.19) as

Equation C.33

where ±t is the variance. For any time increment , the increment of a Brownian motion process, X ( t + ) - X ( t ), has a distribution defined by

Equation C.34

using a variance equal ±t = . This process is used to capture the nature of batch arrival and bursty traffic (see Chapter 18).