Tool 89: Gozinto Chart
| AKA | N/A |
| Classification | Planning/Presenting (PP) |
Tool description
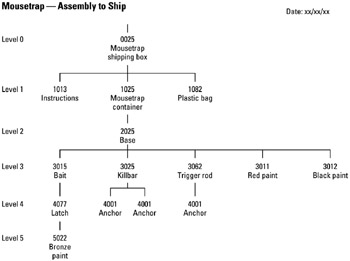
The Gozinto chart is a vertical tree diagram that displays hierarchical levels of detail of a complete product assembly to ship process. Developed by A. Vazsonyi, this project planning tool is of great value for kitting, bill of materials (BOM) auditing, parts/number identification, and operator training.
Typical application
-
To breakdown a product into its parts.
-
To flow out the assembly process.
-
To cross-reference parts data with the hierarchical levels of assembly.
Problem-solving phase
| → | Select and define problem or opportunity |
| → | Identify and analyze causes or potential change |
| Develop and plan possible solutions or change | |
| Implement and evaluate solution or change | |
| Measure and report solution or change results | |
| Recognize and reward team efforts |
Typically used by
| Research/statistics | |
| Creativity/innovation | |
| Engineering | |
| 1 | Project management |
| 3 | Manufacturing |
| Marketing/sales | |
| 4 | Administration/documentation |
| Servicing/support | |
| Customer/quality metrics | |
| 2 | Change management |
before
-
Tree diagram
-
Work breakdown structure (WBS)
-
Information Needs Analysis
-
Process analysis
-
Work flow analysis (WFA)
after
-
Failure Mode and Effect Analysis
-
Task Analysis
-
Potential Problem Analysis
-
Dendrogram
-
Activity analysis
Notes and key points
-
Gozinto chart numbering is by levels and BOM or part identification number. Example: 3015: 3 for level 3, 015 for bill of material or part ID number.
-
This is a similar approach to the work breakdown structure (WBS) chart.
Step-by-step procedure
-
STEP 1 List all parts required to completely assemble the product.
-
STEP 2 Draw a hierarchy of assembly, showing levels of detail from the top down to the basic level of parts.
-
STEP 3 Provide identification of parts; name and number each part charted.
-
STEP 4 Check completeness of chart and date.
Example of tool application
EAN: 2147483647
Pages: 326