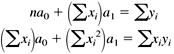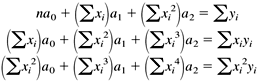10.9 Polynomial Regression
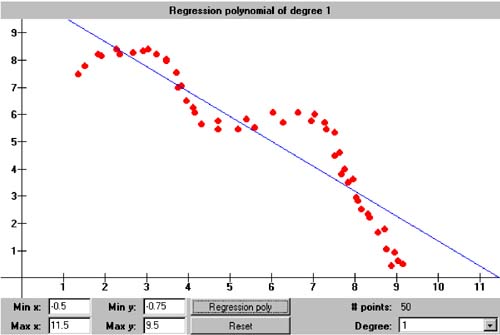
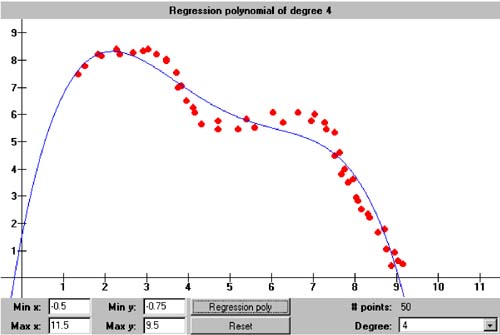
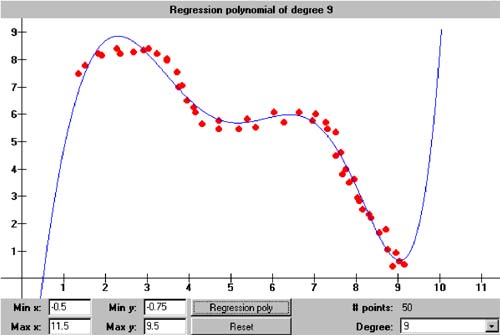
10.9 Polynomial Regression In Chapter 6, we started with the error function for the least-squares regression line: We differentiated this equation twice, first with respect to the unknown coefficient a and then with respect to the unknown coefficient a 1 . We set both derivatives to zero to arrive at the normal equations which we could solve by simple substitution. Now that we've written a class that solves systems of equations, we can compute the coefficients of regression polynomials with higher degrees. For example, a second-degree regression parabola has the error function By differentiating with respect to a , a 1 , and a 2 and setting the derivatives to zero, we get (after the usual algebraic manipulations) the system of three normal equations We can see a pattern emerging! Note that, in the multiplier for a of each equation, the exponent of x i is the row index 0, 1, or 2, and the same exponent for x i appears in the right-hand-side value. (In the first equation, In general, if we want to fit an n th-degree polynomial to a set of at least n +1 data points, the error function is and in the resulting system of normal equations, the r th equation ( r = 0 through n ) has the form Note that, in this linear system, the unknowns are the a i , and the x i are data points used to compute the coefficients of the equations. Class RegressionPolynomial in package numbercruncher.mathutils is analogous to the class RegressionLine , which we saw in Chapter 6. See Listing 10-2a. Listing 10-2a Class RegressionPolynomial . package numbercruncher.mathutils; import numbercruncher.mathutils.IntPower; import numbercruncher.matrix.LinearSystem; import numbercruncher.matrix.ColumnVector; import numbercruncher.matrix.MatrixException; /** * A least-squares regression polynomial function. */ public class RegressionPolynomial implements Evaluatable { /** number of data points */ private int n; /** degree of the polynomial */ private int degree; /** maximum no. of data points */ private int maxPoints; /** true if coefficients valid */ private boolean coefsValid; /** warning message */ private String warningMsg; /** data points */ private DataPoint data[]; /** coefficient matrix A */ private LinearSystem A; /** regression coefficients vector a */ private ColumnVector a; /** right-hand-side vector b */ private ColumnVector b; /** * Constructor. * @param degree the degree of the polynomial * @param maxPoints the maximum number of data points */ public RegressionPolynomial(int degree, int maxPoints) { this.degree = degree; this.maxPoints = maxPoints; this.data = new DataPoint[maxPoints]; } /** * Constructor. * @param degree the degree of the polynomial * @param data the array of data points */ public RegressionPolynomial(int degree, DataPoint data[]) { this.degree = degree; this.maxPoints = maxPoints; this.data = data; this.n = data.length; } /** * Return the degree of the polynomial. * @return the count */ public int getDegree() { return degree; } /** * Return the current number of data points. * @return the count */ public int getDataPointCount() { return n; } /** * Return the data points. * @return the count */ public DataPoint[] getDataPoints() { return data; } /** * Return the coefficients matrix. * @return the A matrix * @throws matrix.MatrixException if a matrix error occurred * @throws Exception if an overflow occurred */ public LinearSystem getCoefficientsMatrix() throws Exception, MatrixException { validateCoefficients(); return A; } /** * Return the regression coefficients. * @return the a vector * @throws matrix.MatrixException if a matrix error occurred * @throws Exception if an overflow occurred */ public ColumnVector getRegressionCoefficients() throws Exception, MatrixException { validateCoefficients(); return a; } /** * Return the right hand side. * @return the b vector * @throws matrix.MatrixException if a matrix error occurred * @throws Exception if an overflow occurred */ public ColumnVector getRHS() throws Exception, MatrixException { validateCoefficients(); return b; } /** * Return the warning message (if any). * @return the message or null */ public String getWarningMessage() { return warningMsg; } /** * Add a new data point: Update the sums. * @param dataPoint the new data point */ public void addDataPoint(DataPoint dataPoint) { if (n == maxPoints) return; data[n++] = dataPoint; coefsValid = false; } /** * Return the value of the regression polynomial function at x. * (Implementation of Evaluatable.) * @param x the value of x * @return the value of the function at x */ public float at(float x) { if (n < degree + 1) return Float.NaN; try { validateCoefficients(); float xPower = 1; float y = 0; // Compute y = a[0] + a[1]*x + a[2]*x^2 + ... + a[n]*x^n for (int i = 0; i <= degree; ++i) { y += a.at(i)*xPower; xPower *= x; } return y; } catch(MatrixException ex) { return Float.NaN; } catch(Exception ex) { return Float.NaN; } } /** * Reset. */ public void reset() { n = 0; data = new DataPoint[maxPoints]; coefsValid = false; } /** * Compute the coefficients. * @throws matrix.MatrixException if a matrix error occurred * @throws Exception if an overflow occurred */ public void computeCoefficients() throws Exception, MatrixException { validateCoefficients(); } /** * Validate the coefficients. * @throws matrix.MatrixException if a matrix error occurred * @throws Exception if an overflow occurred */ private void validateCoefficients() throws Exception, MatrixException { if (coefsValid) return; A = new LinearSystem(degree + 1); b = new ColumnVector(degree + 1); // Compute the multipliers of a[0] for each equation. for (int r = 0; r <= degree; ++r) { float sum = sumXPower(r); int j = 0; if (Float.isInfinite(sum)) { throw new Exception("Overflow occurred."); } // Set the multipliers along the diagonal. for (int i = r; i >= 0; --i) A.set(i, j++, sum); // Set the right-hand-side value. b.set(r, sumXPowerY(r)); } // Compute the multipliers of a[c] for the last equation. for (int c = 1; c <= degree; ++c) { float sum = sumXPower(degree + c); int i = degree; if (Float.isInfinite(sum)) { throw new Exception("Overflow occurred."); } // Set the multipliers along the diagonal. for (int j = c; j <= degree; ++j) A.set(i--, j, sum); } warningMsg = null; // First try solving with iterative improvement. If that // fails, then try solving without iterative improvement. try { a = A.solve(b, true); } catch(MatrixException ex) { warningMsg = ex.getMessage(); a = A.solve(b, false); } coefsValid = true; } /** * Compute the sum of the x coordinates each raised * to an integer power. * @return the sum */ private float sumXPower(int power) { float sum = 0; for (int i = 0; i < n; ++i) { sum += (float) IntPower.raise(data[i].x, power); } return sum; } /** * Compute the sum of the x coordinates each raised to an integer * power and multiplied by the corresponding y coordinate. * @return the sum */ private float sumXPowerY(int power) { float sum = 0; for (int i = 0; i < n; ++i) { sum += (float) data[i].y*IntPower.raise(data[i].x, power); } return sum; } } This class keeps all the data points in array data . Method addDataPoint() appends a new data point to the array. LinearSystem A stores the values of the normal equations (the sums of the powers of the x coordinates), ColumnVector a stores the values of the unknown regression coefficients a i , and ColumnVector b stores the right-hand-side values. In other words, we will be solving the system Aa = b for a. Method getRegressionCoefficients() computes and returns ColumnVector a . Method validateCoefficients() computes the values for A and b . It first tries solving for a with iterative improvement. The computations are especially prone to overflow with higher degrees, so there are special checks for that. If A is nearly singular (which can happen at higher degrees and a low number of data points), iterative improvement will fail to converge. In that case, the method tries solving for a again but without iterative improvement?athe resulting regression polynomial will be less accurate. Method at() computes the value of the regression polynomial for a given value of x . The noninteractive version of Program 10 §C2 creates 20 points along the sine wave from 0 to 2 p . It creates a 3rd-degree regression polynomial for the data points, and then it uses the polynomial to estimate the value of sin p , which should be zero. See Listing 10-2b. Listing 10-2b The noninteractive version of Program 10 §C2. package numbercruncher.program10_2; import numbercruncher.mathutils.DataPoint; import numbercruncher.mathutils.RegressionPolynomial; import numbercruncher.matrix.ColumnVector; import numbercruncher.matrix.MatrixException; /** * PROGRAM 10-2: Polynomial Regression * * Demonstrate polynomial regression by fitting a polynomial * to a set of data points. */ public class Regression { private static final int MAX_POINTS = 20; private static final float TWO_PI = (float) (2*Math.PI); private static final float H = TWO_PI/MAX_POINTS; /** * Main program. * @param args the array of runtime arguments */ public static void main(String args[]) { int degree = 3; float testX = (float) Math.PI; try { RegressionPolynomial poly = new RegressionPolynomial(degree, MAX_POINTS); // Compute MAX_POINTS data points along the sine curve // between 0 and 2*pi. for (int i = 0; i < MAX_POINTS; ++i) { float x = i*H; float y = (float) Math.sin(x); poly.addDataPoint(new DataPoint(x, y)); } // Compute and print the regression polynomial. System.out.print("y = "); ColumnVector a = poly.getRegressionCoefficients(); System.out.print(a.at(0) + " + " + a.at(1) + "x"); for (int i = 2; i <= degree; ++i) { System.out.print(" + " + a.at(i) + "x^" + i); } System.out.println(); // Compute an estimate. System.out.println("y(" + testX + ") = " + poly.at(testX)); // Print the warning if there is one. String warning = poly.getWarningMessage(); if (warning != null) { System.out.println("WARNING: " + warning); } } catch(Exception ex) { System.out.println("\nERROR: " + ex.getMessage()); } } } Output y = -0.14296114 + 1.8568094x + -0.87079257x^2 + 0.09318722x^3 y(3.1415927) = -0.014611721 The interactive version [1] of Program 10 §C2 allows you to plot up to 100 data points with mouse clicks and then create and plot a regression polynomial of degree 1 through 9 among the data points. Screen 10-2 shows screen shots of regression polynomials of various degrees within the same set of data points.
Screen 10-2. Regression polynomials of degree 1, 4, and 9 within the same set of data points. Just as we saw with the interpolation polynomial in Chapter 6, higher degree regression polynomials can have erratic behavior outside of the domain of the data points. |
| |
| Top |
EAN: 2147483647
Pages: 141