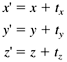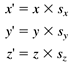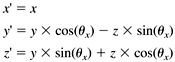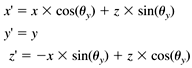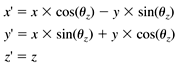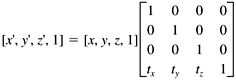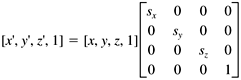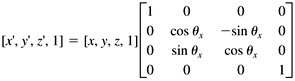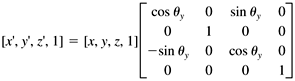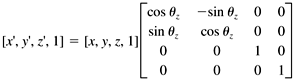9.6 Graphic Transformation Matrices | Java Number Cruncher: The Java Programmers Guide to Numerical Computing

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald Mak
	Table of Contents

	Chapter 9. Basic Matrix Operations

9.6 Graphic Transformation Matrices

With these matrix classes, we can write an interactive program that shows how matrices are used in computer graphics to control the motion of graphic images in three dimensions.

We can represent a three-dimensional graphic image as a set of vertices (corners) and edges (lines between the vertices). Vertices (and the edges between them) can define a flat face three vertices define a triangle, four vertices define a square, and so on.

In three-dimensional space, each vertex has x, y, and z coordinates. We can assume that the z axis extends outward from and into the computer screen, with the positive direction toward the viewer.

We can transform, or alter, the coordinates of a vertex in several ways. The ways our program will use are

Translation . Move the vertex to another location by adding values (positive or negative) to each coordinate value. If all the vertices of a graphic image are similarly translated, the entire image moves to a new location on the screen. We can represent translation mathematically as

where t _x , t _y , and t _z are the translation values for each coordinate.
Scaling . Move the vertex toward or away from the origin by multiplying each coordinate value by a scale factor greater than 1 (away from the origin) or between 0 and 1 (toward the origin). If a graphic image is centered about the origin, and all its vertices are scaled by the same amount in all three dimensions, the image shrinks or grows in size . Mathematically,

where s _x , s _y , and s _z are the scale factors for each coordinate.
Rotation . Move the vertex to a new location on the screen by rotating it around its center of rotation. This rotation can be along the x, y, or z axis. If a graphic image is centered about the origin, and its center of rotation is the origin itself, then rotating all its vertices causes the image to spin along one of the axes. Mathematically, rotation of angle q _x about the x axis is

Rotation of angle q _y about the y axis is

Rotation of angle q _z about the z axis is

If we represent a vertex as a row vector with an appended fourth element with value 1, then we can perform each of the preceding transformations by multiplying the vector by a 4 x 4 transformation matrix :

Translation:
Scaling:
Rotation around the x axis:
Rotation around the y axis:
Rotation around the z axis:

Since scaling is about the origin, we must first move the graphic image to the origin, apply the scaling, and then move the image back to its location. We can do the move to and from the origin with two translation operations. Similarly, to spin the image, it must be at the origin, since we want the center of rotation to be the origin. We can rotate it separately along each axis in turn .

Thus, we can end up multiplying each vertex several times by the various transformation matrices in order to get the sequence of motions we want for the entire image. But there's a wonderful feature of transformation matrices we can multiply all the transformation matrices together in the order that we want to apply them and then multiply each vertex by this product matrix, called the concatenated transformation matrix. That causes the entire sequence of motions to be applied all at once to each vertex.

Top