8.4 A Predictor-Corrector Algorithm

---

 

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald  Mak
	Table of Contents
	Chapter  8.   Solving Differential Equations Numerically

---

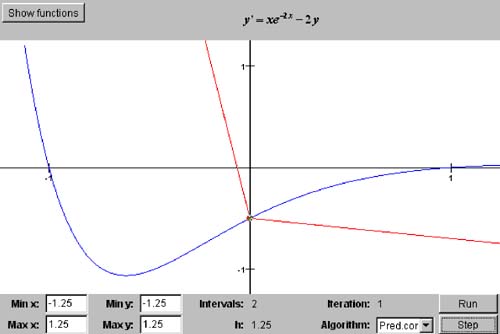
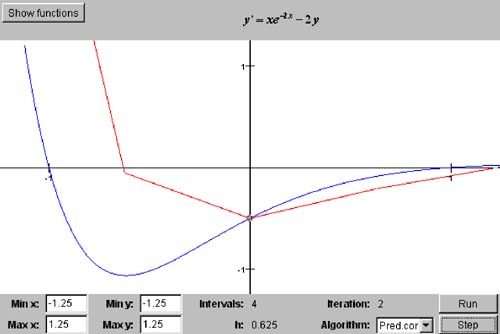
8.4 A Predictor -Corrector Algorithm

How can we improve upon Euler's algorithm? Evidently, using the slope at a point on one side of an interval to compute a point at the other side introduces too great a local error, and so the algorithm converges too slowly before it is overwhelmed by roundoff errors.

A simple predictor-corrector type of algorithm starts out as Euler's algorithm does:

where y ' = f ( x, y ). However, the algorithm considers this to be only a predictor for the next value of y, so we mark it with the 0 superscript. We use this predicted y value (which is at the other side of the interval) to compute the slope there: , where x _{i + 1} = x _i + h. (Euler's algorithm would do this computation at the start of the next interval.)

Now we take the average of the two slopes from both sides of the interval, go back to the beginning of the interval, and use the average slope to compute the corrected next value of y at the other side of the interval:

and x _{i + 1} = x _i + h.

Listing 8-1c shows class PredictorCorrectorDiffEqSolver in package numbercruncher.mathutils , our second subclass of DiffEqSolver . Its nextPoint() method implements the predictor-corrector algorithm.

Listing 8-1c Class PredictorCorrectorDiffEqSolver , the differential equation solver that implements a predictor-corrector algorithm.

 package numbercruncher.mathutils; /**  * Differential equation solver that implements  * a predictor-corrector algorithm.  */ public class PredictorCorrectorDiffEqSolver extends DiffEqSolver {     /**      * Constructor.      * @param equation the differential equation to solve      */     public PredictorCorrectorDiffEqSolver(DifferentialEquation equation)     {         super(equation);     }     /**      * Return the next data point in the      * approximation of the solution.      * @param h the width of the interval      */     public DataPoint nextPoint(float h)     {         float predictor = y + Math.abs(h)*equation.at(x);         float avgSlope  = (equation.at(x, y)                                 + equation.at(x+h, predictor))/2;         y += h*avgSlope;    // corrector         x += h;         return new DataPoint(x, y);     } } 

If we change the command-line argument to the noninteractive version of Program 8 §C1 (review Listing 8-1b) to "predictor," we get output from instantiating a PredictorCorrector DiffEqSolver object. See Listing 8-1d.

Listing 8-1d Output from Program 8 §C1 with the command-line argument "predictor" for the predictor-corrector algorithm.

 ALGORITHM: Predictor-Corrector Differential equation: f(x,y) = 6x^2 - 20x + 11     Initial condition: y(0.0) = -5.0   Analytical solution: y = 2x^3 - 10x^2 + 11x - 5            True value: y(6.0) = 133.0        n              h         y(6.0)          Error -----------------------------------------------------        2            3.0          187.0           54.0        4            1.5          146.5           13.5        8           0.75        136.375          3.375       16          0.375      133.84375        0.84375       32         0.1875      133.21094      0.2109375       64        0.09375      133.05273    0.052734375      128       0.046875      133.01312    0.013122559      256      0.0234375      133.00331   0.0033111572      512     0.01171875      133.00082    8.239746E-4     1024    0.005859375      133.00023   2.2888184E-4     2048   0.0029296875      133.00005   4.5776367E-5     4096   0.0014648438      133.00005   4.5776367E-5 Differential equation: f(x,y) = 2xe^2x + y     Initial condition: y(0.0) = 1.0   Analytical solution: y = 3e^x - 2e^2x + 2xe^2x            True value: y(1.0) = 8.154845        n              h         y(1.0)          Error -----------------------------------------------------        2            0.5       8.449224     0.29437923        4           0.25       8.197649    0.042803764        8          0.125       8.160373   0.0055274963       16         0.0625        8.15547    6.246567E-4       32        0.03125       8.154899    5.340576E-5       64       0.015625       8.154848    2.861023E-6      128      0.0078125       8.154843  -1.9073486E-6      256     0.00390625       8.154846    9.536743E-7      512    0.001953125       8.154843  -1.9073486E-6 Differential equation: f(x,y) = xe^-2x - 2y     Initial condition: y(0.0) = -0.5   Analytical solution: y = (x^2e^-2x - e^-2x)/2            True value: y(1.0) = 0.0        n              h         y(1.0)          Error -----------------------------------------------------        2            0.5   -0.035143584   -0.035143584        4           0.25  -0.0086004995  -0.0086004995        8          0.125  -0.0020729005  -0.0020729005       16         0.0625  -5.0861575E-4  -5.0861575E-4       32        0.03125     -1.2598E-4     -1.2598E-4       64       0.015625   -3.135181E-5   -3.135181E-5      128      0.0078125   -7.822178E-6   -7.822178E-6      256     0.00390625  -1.9620056E-6  -1.9620056E-6      512    0.001953125   -4.900794E-7   -4.900794E-7     1024    9.765625E-4  -1.1298107E-7  -1.1298107E-7     2048   4.8828125E-4  -3.3578544E-8  -3.3578544E-8     4096   2.4414062E-4   -7.399285E-8   -7.399285E-8 

We see that this predictor-corrector algorithm converges faster and produces more accurate solutions than Euler's algorithm. The penalty is a bit more computation at each interval.

Screen 8-1b shows the first three iterations of the interactive version of Program 8 §C1 using this algorithm to solve the same initial value problem as in Screen 8-1a.

Screen 8-1b. The first three iterations of Program 8 §C1 using a predictor-corrector algorithm to solve the initial value problem y' = xe ^{-2 x} - 2 y and y (0) = -0.5. The analytical solution is the smooth curve, and the numerical solution consists of the line segments. The dot represents the initial condition.

---

Top